2.6 Розрахунок стійкості статично невизначеної рами за методом переміщень
2.6.2. Приклад розрахунку
2.6.2. Приклад розрахунку
Визначити критичний параметр навантаження ![]() для рами, показаної на рис. 2.6.1.
для рами, показаної на рис. 2.6.1.
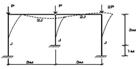
Рисунок 2.6.1 – Розрахункова схема рами
До втрати стійкості в стержнях рами не виникає вигину. При досягненні навантаженням критичного значення вузли рами можуть отримати як кутові, так і лінійні зсуви (можлива форма втрати стійкості показана на рис. 2.6.I пунктиром). При розрахунку рами за методом переміщень, матимемо три невідомих - два кути повороту і одне лінійне зміщення.
Основну систему методу переміщень при розрахунку стійкості подано на рис. 2.6.2.

Рисунок 2.6.2 – Основна система методу переміщень
На рис. 2.6.3 показано епюри згинальних моментів від одиничних поворотів вузлів (рис. 2.6.3, а, б) і від одиничного горизонтального зсуву (рис. 2.6.3, в).
Для всіх трьох стояків рами значення параметра v матимуть різні величини, оскільки поздовжні сили і довжини стояків неоднакові:
для лівого стояка ![]()
для правого стояка ![]()
для середнього стояка ![]()
На одиничних епюрах при функціях ![]() і т.д. в дужках записані ті значення v, яким ці функції відповідають. Оскільки до втрати стійкості вигину не було, то канонічні рівняння однорідні (тобто, вільні члени дорівнюють нулю) і система розрахункових рівнянь для заданої рами матиме вигляд:
і т.д. в дужках записані ті значення v, яким ці функції відповідають. Оскільки до втрати стійкості вигину не було, то канонічні рівняння однорідні (тобто, вільні члени дорівнюють нулю) і система розрахункових рівнянь для заданої рами матиме вигляд:
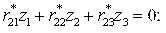 |
(2.6.1) |
Значення коефіцієнтів обчислюють за правилами методу переміщень:
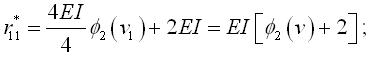

Рисунок 2.6.3 – Епюри моментів в основній системі методу переміщень


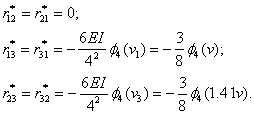
Рівняння стійкості:
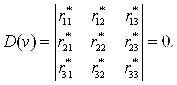 |
(2.6.1) |
Після розкриття визначника з врахуванням того, що ![]() , одержимо
, одержимо
або 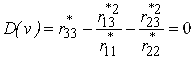 .
.
Після підстановки величин коефіцієнтів одержуємо трансцендентне рівняння стійкості, яке розв'язується за допомогою методу підбору:

Перш ніж задатися якимись значеннями v, доцільно подивитися, в яких межах вони можуть змінюватися. Лівий стояк рами, до параметра функції v якого “прив’язані” параметри решти стояків, знаходиться в умовах, коли її верхній кінець може зміщуватися по горизонталі (при зміщенні чиниться опір жорсткості інших стояків) і пружно повертатися (повертанню чинить опір жорсткість ригеля). Отже, критична сила лівого стояка рами буде вище, ніж для стержня, вигляд якого показаний на рис. 2.6.4, а, і нижче, ніж для стержня, показаного на рис. 2.6.4, б.
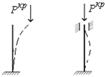
Рисунок 2.6.4 – Вид деформованого стержня при втраті стійкості
Для цих двох граничних випадків знаходимо значення v:
Отже,
Зазначимо, що можливість горизонтальних зсувів значно зменшує жорсткість системи і тому доцільно задатись значенням v більш близьким до нижньої межі, а не до верхньої.
1. v = 2; 1,41v = 2,82; 0,75v =1,5.
За таблицею 1 визначаємо:

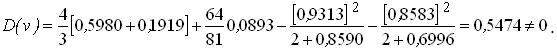
2. v=2,3; 1,41v=3,24; 0,75v=1,72;

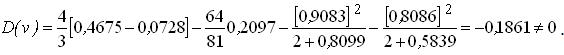
Вважаючи, що в діапазоні 2,0 < v < 2,3 функція D(v) є лінійною, уточнимо значення v, при якому D(v)=0 (рис. 2.6.5).
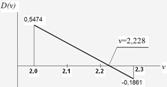
Рисунок 2.6.5 – Наближене знаходження кореня рівняння стійкості шляхом лінійної інтерполяції
За корінь рівняння приймаємо ![]() = 2,228.
= 2,228.
Критичний параметр навантаження
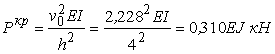 .
.Коефіцієнти вільних довжин стояків рами:
Таблиця 2.6.1 – Значення функцій методу переміщень для стиснуто-зігнутих стержнів
| v | j1(v) | j2(v) | j3(v) | j4(v) | h1(v) | h2(v) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0,00 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
| 0,2 | 0,997 | 0,998 | 1,001 | 0,999 | 0,984 | 0,996 |
| 0,4 | 0,989 | 0,994 | 1,003 | 0,997 | 0,936 | 0,984 |
| 0,6 | 0,986 | 0,988 | 1,006 | 0,994 | 0,856 | 0,964 |
| 0,8 | 0,957 | 0,979 | 1,011 | 0,989 | 0,743 | 0,936 |
| 1,00 | 0,931 | 0,966 | 1,017 | 0,983 | 0,598 | 0,900 |
| 1,10 | 0,916 | 0,959 | 1,021 | 0,980 | 0,513 | 0,879 |
| 1,2 | 0,900 | 0,951 | 1,025 | 0,975 | 0,420 | 0,856 |
| 1,3 | 0,881 | 0,942 | 1,030 | 0,971 | 0,318 | 0,831 |
| 1,4 | 0,861 | 0,933 | 1,035 | 0,967 | 0,208 | 0,803 |
| 1,5 | 0,833 | 0,923 | 1,040 | 0,962 | 0,089 | 0,774 |
| 1,6 | 0,815 | 0,912 | 1,046 | 0,957 | -0,038 | 0,743 |
| 1,7 | 0,789 | 0,900 | 1,053 | 0,951 | -0,174 | 0,710 |
| 1,8 | 0,761 | 0,877 | 1,060 | 0,945 | -0,319 | 0,675 |
| 1,9 | 0,730 | 0,873 | 1,068 | 0,938 | -0,474 | 0,637 |
| 2,0 | 0,696 | 0,859 | 1,076 | 0,931 | -0,637 | 0,598 |
| 2,10 | 0,660 | 0,844 | 1,085 | 0,924 | -0,810 | 0,556 |
| 2,2 | 0,620 | 0,827 | 1,095 | 0,916 | -0,993 | 0,513 |
| 2,3 | 0,577 | 0,810 | 1,105 | 0,908 | -1,186 | 0,467 |
| 2,4 | 0,530 | 0,791 | 1,116 | 0,900 | -1,389 | 0,420 |
| 2,5 | 0,479 | 0,772 | 1,129 | 0,891 | -1,604 | 0,370 |
| 2,6 | 0,423 | 0,751 | 1,142 | 0,881 | -1,830 | 0,318 |
| 2,7 | 0,362 | 0,729 | 1,156 | 0,872 | -2,068 | 0,264 |
| 2,8 | 0,294 | 0,706 | 1,171 | 0,861 | -2,319 | 0,208 |
| 2,9 | 0,219 | 0,682 | 1,188 | 0,851 | -2,584 | 0,150 |
| 3,00 | 0,136 | 0,656 | 1,206 | 0,840 | -2,864 | 0,089 |
| 3,10 | 0,042 | 0,629 | 1,225 | 0,827 | -3,161 | 0,021 |
| 3,2 | -0,063 | 0,600 | 1,246 | 0,815 | -3,478 | -0,038 |
| 3,3 | -0,185 | 0,569 | 1,269 | 0,802 | -3,815 | -0,105 |
| 3,4 | -0,325 | 0,537 | 1,294 | 0,789 | -4,178 | -0,174 |
| 3,5 | -0,489 | 0,502 | 1,321 | 0,775 | -4,573 | -0,246 |
| 3,6 | -0,686 | 0,466 | 1,351 | 0,761 | -5,006 | -0,319 |
| 3,7 | -0,9,27 | 0,426 | 1,383 | 0,746 | -5,490 | -0,395 |
| 3,8 | -1,230 | 0,325 | 1,419 | 0,730 | -6,044 | -0,474 |
| 3,9 | -1,627 | 0,341 | 1,458 | 0,713 | -6,697 | -0,554 |
| 4,00 | -2,173 | 0,293 | 1,502 | 0,696 | -7,506 | -0,637 |
| 4,10 | -2,981 | 0,242 | 1,550 | 0,678 | -8,584 | -0,722 |
| 4,2 | -4,315 | 0,188 | 1,604 | 0,660 | -10,20 | -0,810 |
| 4,3 | -6,995 | 0,129 | 1,664 | 0,640 | -13,14 | -0,900 |
| 4,4 | -15,33 | 0,065 | 1,731 | 0,620 | -27,78 | -0,993 |
| 4,5 | 227,8 | -0,005 | 1,807 | 0,599 | 221,05 | -1,088 |
| 4,6 | 14,67 | -0,081 | 1,893 | 0,577 | 7,616 | -1,186 |
| 4,7 | 7,818 | -0,165 | 1,992 | 0,554 | 0,455 | -1,286 |
| 4,8 | 5,402 | -0,257 | 2,106 | 0,530 | -2,278 | -1,389 |
| 4,9 | 4,146 | -0,361 | 2,235 | 0,505 | -3,8557 | -1,495 |
| 5,00 | 3,361 | -0,477 | 2,392 | 0,479 | -4,972 | -1,604 |
| 5,10 | 2,813 | -0,610 | 2,576 | 0,452 | -5,857 | -1,715 |
| 5,2 | 2,399 | -0,763 | 2,796 | 0,423 | -6,655 | -1,830 |
| 5,3 | 2,067 | -0,942 | 3,065 | 0,393 | -7,296 | -1,947 |
| 5,4 | 1,788 | -0,156 | 3,399 | 0,362 | -7,932 | -2,068 |
| 5,5 | 1,545 | -1,418 | 3,823 | 0,329 | -8,538 | -2,192 |
| 5,6 | 1,326 | -1,748 | 4,379 | 0,294 | -9,127 | -2,319 |
| 5,7 | 1,123 | -2,180 | 5,135 | 0,258 | -9,706 | -2,449 |
| 5,8 | 0,930 | -2,778 | 6,214 | 0,219 | -10,28 | -2,584 |
| 5,9 | 0,742 | -3,668 | 7,873 | 0,179 | -10,86 | -2,723 |
| 6,00 | 0,555 | -5,159 | 10,73 | 0,136 | -10,44 | -2,864 |
| 6,1 | 0,366 | -8,2355 | 16,74 | 0,091 | -12,04 | -3,010 |
| 6,2 | 0,170 | -18,59 | 37,31 | 0,042 | -12,64 | -3,161 |
| 6,28 | 0,000 | -∞ | +∞ | 0,000 | -13,03 | -3,290 |


