ЗА МЕТОДОМ СКІНЧЕННИХ ЕЛЕМЕНТІВ
4.3 Приклади розрахунку рами за МСЕ
4.3.1 Запис статичних рівнянь. Компоновка матриці умов рівноваги (матриці форми [A])
4.3.1 Запис статичних рівнянь. Компоновка матриці умов рівноваги (матриці форми [A])
У стержневій системі 2 типи СЕ: стержні і вузли. Сукупність рівнянь рівноваги для кожного стержня і вузла можна розглядати як систему рівнянь рівноваги всієї системи. До вузлів дискретної моделі відносяться точки поєднання стержнів, місця зміни жорсткості стержня чи зміни величини інтенсивності розподіленого навантаження, точки прикладання зосереджених сил чи моментів, опорні вузли.
Для запису рівнянь рівноваги вузлів доцільно застосовувати загальну систему координат, для запису рівнянь рівноваги стержнів зручно обирати свою власну, місцеву систему координат.
Розбиваємо розрахункову схему рами на скінченні елементи (рис. 4.2).
Умови рівноваги:
Вузол 1
∑ Fx = 0 → H1 + N1-2∙cosα + Q1-2∙sinα = 0;
∑ Fy = 0 → V1 + N1-2∙sinα – Q1-2 ∙cosα = 0;
∑ M1 = 0 → - M1-2 = 0.
Стержень 1 - 2
∑ Fx1 = 0 → - N1-2 +N2-1 = 0;
∑ Fy1 = 0 → Q1-2 – Q2-1 -qℓ1-2 = 0;
∑ M1 = 0 → Q2-1 ∙ ℓ1-2 + М1-2 – M2-1 + qℓ²1-2 /2 = 0.
Вузол 2
∑ Fx = 0 →P∙cos β + N2-3=0, ∑ Fy = 0 →q∙sin β – Q2-3=0,
∑ M2 = 0 →M2-3 – M2-1=0β.
Стержень 2-3
∑ Fx1 = 0 → - N2-3 +N3-2 = 0,
∑ Fy1 = 0 → Q2-3 – Q3-2 -qℓ1-2 = 0, ∑ M1 = 0 → Q1-2 ∙ ℓ2-3 + M2-3 –М1-2 = 0.
Вузол 3
. . .
Стержень 3-4 . . .
Таблиця 4.1 – Матриця форми [A]
| V1 | H1 | N1-2 | Q1-2 | M1-2 | N2-1 | Q2-1 | M2-1 | N2-3 | Q2-3 | M2-3 | ... | Вільні члени |
| 0 | 1 | cos a | sin a | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 |
| 1 | 0 | sin a | -cos a | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 |
| 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0 |
| 0 | 0 | -1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | ... | ql1-2 |
| 0 . |
0 . |
0 . |
0 . |
1 . |
0 . |
l1-2 . |
-1 . |
0 . |
0 . |
0 . |
... . |
-ql21-2/2 ..... |
Таблиця 4.1 включає коефіцієнти матриці умов рівноваги [A] ×{S} = {P}.
Остання колонка (вільні члени) – це вектор зовнішнього навантаження {P} = {0, 0, 0, 0, qℓ1-2, -qℓ²1-2/2,…}.
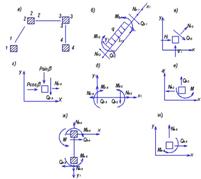
Рисунок 4.2 – Розбивка рами на СЕ (а) та зусилля в стержнях 1-2, 3-4, 5-6 і вузлах 1, 2, 3, 4, (б-и)
Вектор шуканих внутрішніх зусиль
{S} = { V1, H1, N1-2, Q1-2, M1-2,…}.
Матриця умов рівноваги матиме стільки рядків, скільки умов рівноваги
(m) і стільки стовпців, скільки невідомих (k):
 |
(4.3.1) |
За умови m = k маємо статично визначену розрахункову схему системи,
при m < k – система статично невизначена,
при m > k – геометрично змінна.


