ЗА МЕТОДОМ СКІНЧЕННИХ ЕЛЕМЕНТІВ
4.3 Приклади розрахунку рами за МСЕ
4.3.3 Фізичні рівняння. Компонування матриці піддатливості та жорсткості для стержня
4.3.3 Фізичні рівняння. Компонування матриці піддатливості та жорсткості для стержня
Розглянемо стержень i–j, навантажений згідно з рис. 4.1.3 силами N, Mi, Mj. Деформацію стержня характеризує три компоненти: кути повертання в точках i, j – φi, φj та лінійне переміщення Δl.Фізичне рівняння, що встановлює зв’язок між зусиллями та деформаціями для одного стержня
| {ε}e = [d] e ∙ {S}e , | (4.3.4) |
де {ε}e ={φi, φj, Δl}T– вектор деформацій стержня;
{S}e= {Mi, Mj, N}T– вектор кінцевих зусиль в стержні;
[d] e – матриця співвідношень закону Гука для стержня le.
Розгорнутий матричний запис для одного стержня е (рис. 4.1.3).
 . . |
(4.3.5) |
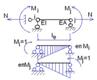
Рисунок 4.3 – Пояснення до компонування матриці піддатливості стержня le
Лінійна компонента деформацій, лінійне подовження Δle за умови пружної роботи стержня:
| Δle=N |
(4.3.6) |
На стержень le крім поздовжньої сили N діють ще згинальні моменти (Mi, Mj). В такому випадку дії декількох сил кутові деформації стержня φі , φj можна знайти на основі принципу суперпозицій через одиничні переміщення
| φi=δiiMi+δijMj | (4.3.7) |
| φj=δjjMi+δijMj | (4.3.8) |
Одиничні переміщення δіj знаходяться за відомими формулами Максвела–Мора.
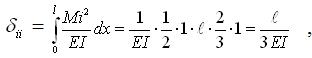 |
(4.3.9) |
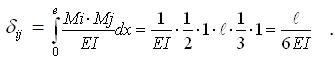 |
(4.3.10) |
Матриця співвідношень закону Гука для стержня ℓе:
[d]e = 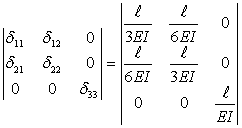 . . |
(4.3.11) |
Для всієї системи (4.1.7):
де |D| – матриця піддатливості, матриця одиничних переміщень, тобто переміщень, що зумовлені одиничними узагальненими силами. Під узагальненим переміщенням розуміють будь-яке переміщення, незалежно від його характеру або причини, що його зумовлює (тобто переміщення в загальному розумінні цього слова). Кожному переміщенню ставиться у відповідність однозначна силова дія, що здійснює роботу на цьому переміщенні – це узагальнена сила.
Матриця піддатливості всієї рами складається із трьох складових матриць піддатливості кожного стержня і має вигляд:
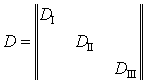 .
.Матриця, обернена до матриці піддатливості має назву матриця жорсткості:
| (4.3.12) |
За алгоритмом, наведеним вище, для вхідних параметрів Р=80 кН, a=60° , β=45°, h=3,46 м, q=20 кН/м, М=0 отримані такі значення внутрішніх зусиль (рис. 4.1.4):
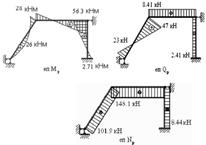
Рисунок 4.4 – Епюри внутрішніх зусиль в раміle
Приклад 2. Розрахунок рами методом скінченних елементів

Рисунок 4.5 – Задана рама
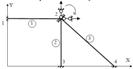
Рисунок 4.6 – Основна система МСЕ
![]() 5,381 м.
5,381 м.
1. Будуємо основну систему МСЕ и нумеруємо вузли і стержні рами.
Оскільки в МСЕ враховуються осьові деформації стержнів, то на жорсткі вузли накладаємо три в’язі, що відповідають трьом переміщенням вузла: вертикальному, горизонтальному і кутовому.
Рама має три скінченних елементи (стержні) и чотири вузли. Координати вузлів в загальній системі координат:
1 – х=0; у=3,6; 2 – х=3; у=3,6;
3 – х=3; у=0; 4 – х=7; у=0.
2. Будуємо матриці жорсткості стержнів і вектори вузлових навантажень у місцевій системі координат, коли вісь x' спрямована уздовж осі стержня, а вісь y' - перпендикулярно до осі стержня.
Кожний стержень має по три невідомих переміщення ![]() в кожному вузлі.
в кожному вузлі.
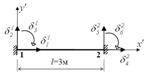
Рисунок 4.7 – Схема вузлових переміщень СЕ № 1
Стержень 1 (рис. 4.7).
Стержень 1 має жорстке защемлення с двох сторін.
Матриця жорсткості СЕ №1 має вигляд:


Навантаження, прикладене до стержня, зосереджуємо в вузлах. Вектор вузлового навантаження в місцевій системі координат має вигляд:
{p'}1=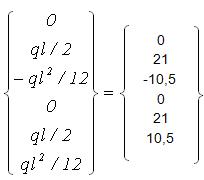
Стержень 2 (рис. 4.8).
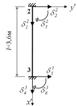
Рисунок 4.8 – Схема вузлових переміщень СЕ №2
Для стержня 2 матриця жорсткості обраховується за тими ж формулами, що і для стержня 1. Вектор вузлових навантажень нульовий, оскільки до стержня не прикладене навантаження.
[K']2 = 
Стержень 3 (рис. 4.9).
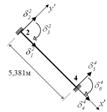
Рисунок 4.9 – Схема вузлових переміщень СЕ №3
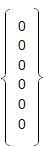
[K']3 = 
3. Будуємо матриці перетворень для кожного стержня.
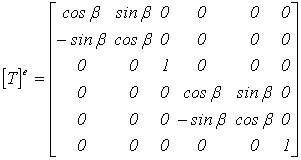
де β - кут між напрямом осі х загальної системи координат і напрямом осі x' місцевої системи координат.
Для стержня 1 матрицю перетворень записувати не потрібно, оскільки в цьому випадку місцева система координат збігається з загальною системою координат.
Стержень 2.

Стержень 3.

4. Будуємо матриці жорсткості в загальній системі координат:
Перемноження матриць виконуємо на комп’ютері за допомогою програми EXCEL.
[K]1=[K']1=
[K]2=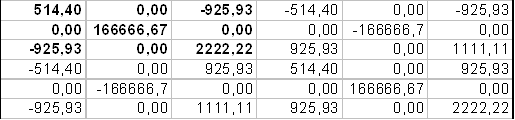
[K]3=
5. Перетворимо вектори вузлових навантажень із місцевої системи координат в загальну.
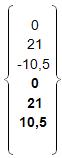 ; {p}2=
; {p}2=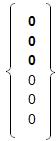 ;{p}3=
;{p}3=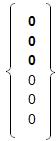 .
.6. Будуємо матрицю жорсткості для всієї рами в загальній системі координат.
Матриці жорсткості для трьох елементів рами можна подати в вигляді:
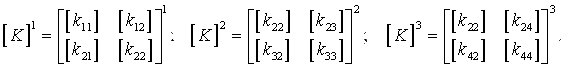
Оскільки невідомими є переміщення вузла 2, то загальну матрицю жорсткості отримуємо, додаючи елементи матриць [k22]. В матрицях ці елементи виділені жирним шрифтом.
 .
.7. Формуємо вектор вузлових навантажень в загальній системі координат.
Вектори вузлових навантажень для трьох стержнів рами можна подати в вигляді:
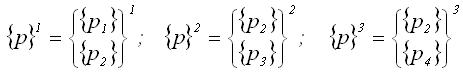
Вектор навантаження в вузлі 2 отримаємо, додаючи елементи {p2}.
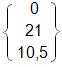 .
.8. Записуєм систему рівнянь рівноваги для вузла 2.
Розв’язуючи систему рівнянь, отримуємо вектор переміщень вузла 2.
 .
.
9. Записуємо вектори вузлових переміщень для кожного стержня в загальній системі координат.
 ; {δ}2=
; {δ}2= ; {δ}3=
; {δ}3= .
.10. Визначаємо вузлові зусилля в стержнях в місцевій системі координат.
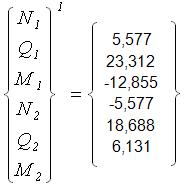 ;
;
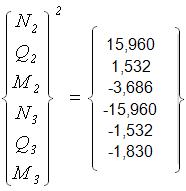 ;
;
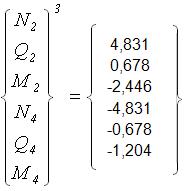 .
.
11. За обрахованими значеннями будуємо епюри M, Q, N (рис. 4.10-4.12).
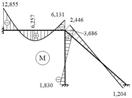
Рисунок 4.10 – Епюра згинальних моментів
Величину моменту в середньому перетині стержня 1 обраховуємо за формулою:
Перевіряємо рівновагу вузла рами
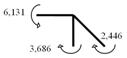
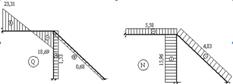
Рисунок 4.11 – Епюра поперечних сил Рисунок 4.12 – Епюра поздовжніх сил


