Знаходження власних чисел матриці «с» шляхом розкриття визначника
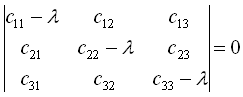
1. Розкриваючи визначник одержуємо кубічне рівняння
де ![]()
![]() ;
;
![]() .
.
2. Виконуючи в кубічному рівнянні заміну x=λ+a1/3, одержуємо зведене рівняння
де p=a2-a21/3; q=2a31/27-a1a2/3+a3.
3. Обчислюємо дискримінант рівняння
Кубічне рівняння має три дійсних корені в випадку D≤0. Якщо D>0 - елементи матриці с обчислені неправильно.
4. Обчислюємо корені зведеного рівняння
φ=arccos(-q/2u3);
x1=2ucos(φ/3);
x2=2ucos(φ/3-2π/3);
x3=2ucos(φ/3+2π/3)
5. Обчислюємо власні числа матриці с
λ2=x2-a1/3;
λ3=x3-a1/3.
3. Виконуємо перевірку правильності обчислення власних чисел шляхом їх підстановки в кубічне рівняння.


