12 ЗАТОПЛЕНІ ТУРБУЛЕНТНІ СТРУМЕНІ

12.1 Визначення, поняття і залежності процес розповсюдження газу, який витікає із сопла чи отвору в заповнене газом довкілля, називається струминним процесом, а сам газ, що витікає, і частинки утягненого їм в рух навколишнього середовища - струминою.
Струмина, яка не обмежена твердими стінками, називається вільною.
Струмина вважається затопленою, якщо вона розповсюджується в просторі зайнятим однорідною рідиною (крапельною чи газоподібною).
Теоретичні та експериментальні дослідження показали таке. Струмина, яка виходить із отвору з насадкою в умовах плавного окреслення  (контуру) входу в насадок і при умові, що тиск на виході із нього не нижче  «критичного» (на випадок витікання газу), поступово розширюється у вигляді конусу і завдяки в’язкості утягує в рух рідину, яка її оточує. Таким чином струминою і довкіллям відбувається обмін масою. Так що в направленні руху струмини її маса збільшується.

В вихідному перерізі сопла (круглого рдіусом r0, прямокутного – напівшириною b0) ab – uо = const (рис. 12.1). В області трикутника abc у всіх точках струмини швидкості рідини рівні між собою і рівні uо, це ядро струмини.

На межових лініях (рис. 12.1) ON і ON? повздовжні швидкості дорівнюють нулю; ці лінії перетинаються на осі в точці О, яка називається «полюсом».
Ізотахи (рис. 12.2) – лінії рівних відносних швидкостей в області основної ділянки струмини (рис. 12.3).
В різних перерізах (рис. 12.4) поле швидкостей безперервно деформується. Чим далі переріз від початку струмини, тим нижча і ширша епюра швидкостей. Інакше кажучи, підтверджується загальна картина поступового розширення струменя і зменшення її швидкості.
Якщо всі ці дані представити в безрозмірних координатах для  круглої і для плоскої струмини виявляється така цікава обставина: всі дослідні точки для любих перерізів вкладаються на одну загальну криву (рис. 12.5). Тобто швидкості в подібних точках різних перерізів струмини подібні між собою.

Іншими словами, закономірність розподілення швидкостей і, отже, епюри повздовжніх осереднених швидкостей мають однаковий характер для всіх перерізів основної ділянки струмини.

Для круглої трубки епюра швидкостей добре апроксимується функцією помилок, тобто виразом вигляду
,                                    (12.1)
де  с-деяка стала (із дослідів).
Для круглої і плоскої струмини: визначається із дослідів.
Таблиця 12.1 – Розрахункові формули (по Абрамову Г.Н.) для круглої і плоскої вільної струмини

Параметри струмини	Позначення	Розрахункові формули струмини
		кругла	плоска
Кут нахилу (на один бік) умовної зовнішньої межі	q/2	3,4a	2,4a
Відносна довжина початкової ділянки	lo/ro; lo/bo	0,67/a	1,03/a
Відносний радіус (на півширина)	r/ro; b/bo	3,4[0,29+(al/ro)]
Відносна осьова швидкість на основній ділянці	umax/u	0,96/[0,29+(al/ro)]
Відносні витрати на основній ділянці	Q/Qo	2,18/[0,29+(al/ro)]

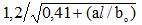
a – константа; в рівномірному початковому полі швидкостей а = 0,066 для круглої і а = 0,09 – для плоскої струмини. При цьому кут нахилу зовнішньої умовної межі відповідно дорівнює 13о і 15о для круглої і плоскої струмини.
Відповідно:         При розвинутій початковій епюрі швидкостей (рівномірний турбулентний потік в круглій трубі) – а = 0,07. В цих формулах довжина l означає відстань від початку струмини, яка в загальному випадку не співпадає з відстанню х від “полюса” 0.
При більш детальних розрахунках струменів користуються співвідношеннями, які наведені в табл..12.2 і 12.3.
Безрозмірний коефіцієнт структури  а  враховує вплив нерівномірності розподілу швидкостей в початковому перерізі і ступінь турбулентності потоку на параметри струменя. Наближені значення цього коефіцієнту для сопла – 0,07, для плоского струменя – 0,09...0,12 (таблиця 12.2), для циліндричної труби – 0,76 (таблиця 12.3).
Розподіл швидкостей в струмені можна також розрахувати за формулою Шліхтінга
                                       (12.2)
де – відносна ордината точки, для круглого струменя для плоского .

Таблиця 12.2 – Розрахункові формули для плоского струменя

           В таблиці 12.2 відносні величини:   

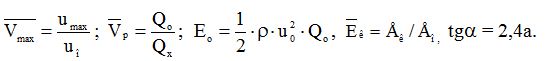
Таблиця 12.3 – Розрахункові формули для круглого струменя

В таблиці 12.3 відносні величини:   (aк – коефіцієнт Коріоліса), tga = 3,4a.
Взаємодія струменів. Зміною кута зустрічі двох стикаючихся струмин, які витікають в необмежений простір, вдається змінити форму, характер затухання швидкості і напрямок руху струмини, що утворилася при стиканні, яка злилася.
В полум’яних печах, використовуючи опалення за допомогою направлених під кутом одне до одного пальних пристроїв, можна змінювати форму і довжину як аеродинамічного факела, так і факела горіння в порівнянні з опаленням одним пальником. Розв’язувати такі задачі аналітичним методом не вдається.
Із практики встановлено: далекобійність результуючого струменя зменшується зі збільшенням кута зустрічі струменів, що стикаються. Це наслідок зміни рівня турбулентності вздовж вісі результуючої струмини.
А також збільшується відношення периметру струмини до її перерізу. В результаті чого із навколишнього нерухомого середовища втягується більша маса газу, котра діє з більшою гальмівною дією.
При проектуванні газових пальників важливо вміти розрахувати процес розвитку і змішування струменів. Наводимо деякі розрахункові співвідношення для круглого і прямокутного струменів (рис. 12.6 ):

           а) рівняння для вісі круглого струменя
                 (12.3)
справедливо при
                               (12.4)
б) глибина проникнення круглого струменя в потік

     (12.5)
в) рівняння вісі прямокутного струменя
                        (12.6)
де   – еквівалентний діаметр струменя;
– площа сопла;
г) глибина проникнення прямокутного струменя в потік
,                                    (12.7)
велика сторона сопла при цьому направлена паралельно швидкості u1.