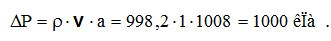8 ГІДРАВЛІЧНИЙ УДАР В ТРУБАХ

8.2 Приклади

           8.2.1. Визначити найменший час закриття засувки tз = tmin, щоб підвищення тиску в кінці трубопроводу, яке покликане гідравлічним ударом було не більше Вода витікає із резервуара по горизонтальному новому сталевому трубопроводу довжиною l, з внутрішнім діаметром d і товщиною стінки d. Рівень води в резервуарі над центром труби Н. Температура води t = 20оС, коефіцієнт тертя за довжиною труби l. Чому буде дорівнювати підвищення тиску на випадок миттєвого закриття засувки в трубопроводі?

           Розв’язок

На рис. 8.3 представлена розрахункова схема: 0-0 – площина порівняння; 1-1 –і 2-2 – перерізи за рухом води.
Рівняння Бернулі для цілого потоку вязкої рідини
                          
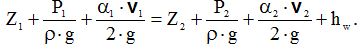
Згідно рис. 8.3:
Тоді рівняння Бернулі приймає вигляд при a2 = 1
.                                                
Втрати напору між перерізами 1-1 і 2-2
                              
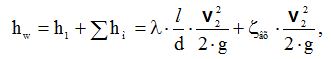
де V – середня швидкість в трубі, м/с;
– коефіцієнт місцевого опору входу,
Розвязуємо рівняння Бернулі відносно V2
                                  
                        
    
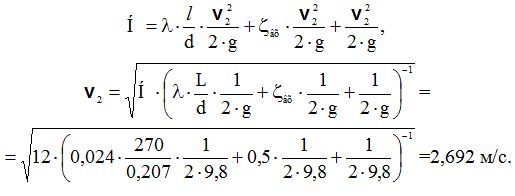
Для непрямого гідравлічного удару (t3 > T)
                                             
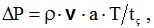
де V – середня швидкість води в трубі, V = V2 = 2,692 м/с;
а – швидкість розповсюдження ударної хвилі в трубопроводі, м/с;
                         
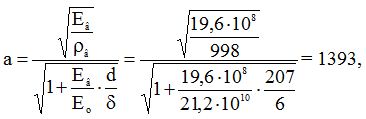
де Ев – модуль об’ємної пружності води, при Па (табл. А.1.2);
Ео – модуль об’ємної пружності матеріалу стінок труби, сталь (табл. А.1.6);

Т – період гідравлічного удару,
Приймаємо і визначаємо час закриття засувки
                
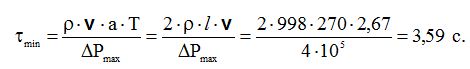
В результаті миттєвого закриття засувки підвищення тиску складатиме
.                       
Отже, у випадку миттєвого закриття засувки підвищення тиску в n разів перевищує допустиме
.                             
           8.2.2. Система  складається з двох послідовно зєднаних сталевих трубопроводів (діаметри трубопроводів: d1 = 200 мм, d2 = 100 мм; довжини: l1= 100 м, l2 = 200 м) і засувки, яка встановлена в кінці системи (рис.8.4). Витрата води Товщина стінок трубопровода температура води t = 20оС.
1. Визначити підвищення тиску перед засувкою, якщо її закрити за час
2. Визначити найменший час закриття засувки, який виключає прямий гідравлічний удар.
           Розв’язок

Спочатку графічно представте розрахункову схему.
Найменший час закриття засувки, який необхідний для попередження прямого гідравлічного удару, знаходимо за формулою
.                                               
Швидкість ударної хвилі визначається за формулою
                                       

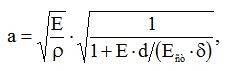
Для першого трубопровода
           
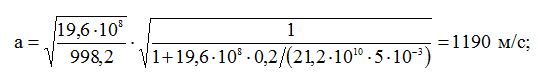
для другого трубопровода
           
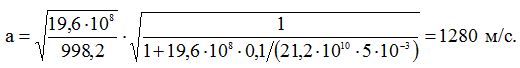
Тоді
                             
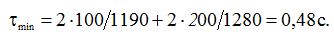
Заданий час закриття засувки t менший, ніж мінімальний час закриття tmіn, який необхідний для попередження прямого удару.
Таким чином, буде спостерігатись прямий гідравлічний удар, при якому підвищення тиску можна визначити за формулою
.                                                 
Швидкість руху води в трубопроводі до закриття засувки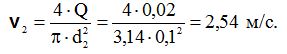

        

 

Отже

.                         
           8.2.3. Визначити підвищення тиску , що виникає при раптовому закритті засувки на водопровідній трубі, якщо швидкість руху води 1 м/с. Швидкість розповсюдження ударної хвилі с прийняти рівній 1000 м/с.
           Розв’язок
Для визначення миттєвого підвищення тиску скористаємося формулою (8.3)
.                               
8.2.4. В сталевій водопровідній трубі діаметром d = 0,5 м і товщиною стінок вода рухається зі швидкістю v = 1 м/с. Визначити величину підвищення тиску після миттєвого перекриття труби.
           Розв’язок
Швидкість розповсюдження ударної хвилі визначаємо за формулою
                                     
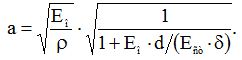
Значення модуля пружності води – (див. табл. A.1.2), модуля пружності матеріалу стінок труби – (див. табл. A.1.6), (див. табл. A.1.12)
              
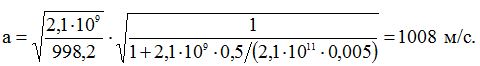
Величину підвищення тиску визначаємо за формулою