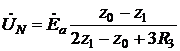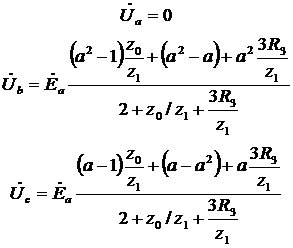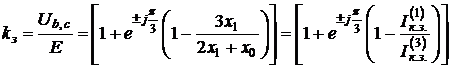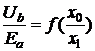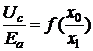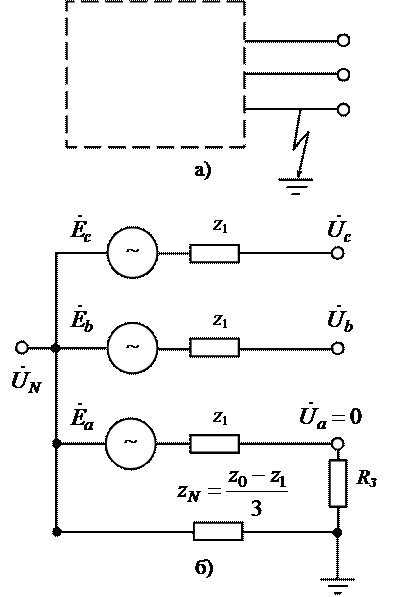
3 Внутрішні перенапруги та їх обмеження

3.3 Підвищення напруги на здорових фазах при однофазних замиканнях

Однією з основних причин застосування заземленої нейтралі в мережах напругою 110 кВ і вище є ізоляційна проблема; заземлення нейтралі обмежує підвищення напруги на здорових фазах при однофазних коротких замиканнях. Розглянемо це питання детальніше.

На рис. 3.4,а наведено структурну схему мережі, в якій відбулося однофазне коротке замикання. Побудуємо для неї універсальну комплексну схему. Така схема показана на рис. 3.4,б. Напруги  є еквівалентними джерелами симетричної напруги,  і  — еквівалентними опорами у каналах прямої і нульової послідовностей. Фаза а заземлена через опір заземлення , фази b і с ізольовані.

Рисунок 3.4 – Універсальна комплексна схема для несиметричної комутації – однофазного короткого замикання:

а) початкова схема; б) розрахункова схема

Відповідно до схеми на рис. 3.4,б напруги здорових фаз рівні:

,

а

.

Підставляючи значення  і враховуючи, що  утворюють симетричну трійку векторів, отримуємо:

                                                (3.9)

де .

Зазвичай можна нехтувати активними опорами прямої послідовності, тобто прийняти . Активні опори нульової послідовності мають істотну величину, і тому приймається .

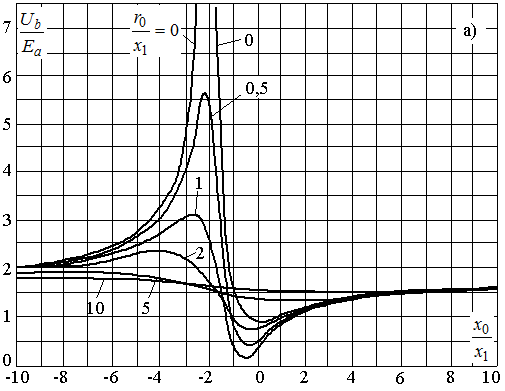
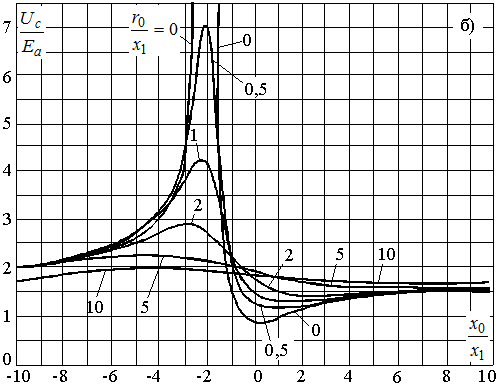
На рис. 3.5 наведено криві залежностей напруги U_b/E_a і U_c/E_a від відношення реактивних опорів x₀/x₁ при різних r₀/x₁ і . Позитивним x₀/x₁ відповідає область заземленої нейтралі системи, негативним x₀/x₁, коли  має ємнісний характер, відповідає область ізольованої нейтралі. Як видно з кривих, напруга на фазі c вища, ніж на фазі b, і вони однакові тільки при r₀=0. Відношення U_b/E_a та U_c/E_a, що характеризують підвищення напруги на здорових фазах при однофазних коротких замиканнях, позначаються через коефіцієнт заземлення .

В області заземленої нейтралі зі зростанням x₀/x₁ і r₀/x₁ напруги U_b/E_a та U_c/E_a зростають, прямуючи при х₀®¥ або r₀® ¥ до .

Зазвичай, в розрахунках перенапруг нехтують активними опорами і, відповідно, приймають z₀/z₁=x₀/x_1. В цьому випадку U_b=U_c.

Використовуючи будь-яку з формул (3.9), знаходимо:

           ,  (3.10)

де  і  – значення струмів однофазного і трифазного короткого замикання в точці комутації. Формула (3.10) зручна в розрахунках, оскільки струми короткого замикання в мережах зазвичай відомі. Формулі (3.10) відповідають кривій r₀/x₁=0 в правій області рис. 3.5.

Рисунок 3.5 – Криві залежності напруги на здорових фазах b і с від відношення x₀/x₁ для різних r₀/x₁ при однофазному короткому замиканні на фазі,

а) криві ; б) криві ; z₁=0+jx₁; z₀=r₀+jx₀

Області ефективно заземленої нейтралі відповідають значення . За кривими на рис. 3.5 або за формулою (3.10) знаходимо, що  і  відповідає k_З =1,25. З урахуванням того, що  і , нормами для вибору ізоляції встановлено підвищення напруги робочої частоти на здорових фазах до .

В області ізольованої нейтралі при значенні  виникає резонанс. Резонанс виникає між індуктивним опором прямої послідовності і ємнісним опором нульової послідовності (опором ємностей фаз на землю). Напруги на здорових фазах згідно з кривими на рис. 3.5 зростають до дуже високих значень. Практично подібний резонанс можливий тільки в дуже розгалужених кабельних мережах, які живляться відносно малопотужним джерелом. Але в таких мережах, як правило, встановлюється дугогасильна котушка, що різко підвищує  мережі. При  прямує до . Отже, в нескінченності область значень кривих на рис. 3.5 в правій і лівій областях зливаються.

Криві на рис. 3.5 належать випадку . Вплив опору заземлення  показаний кривими на рис. 3.6. На осі ординат відкладено відношення , де U_тах - максимальна напруга на фазах b і с. При зростанні R_З/x₁ до одиниці коефіцієнт k_З зростає. Подальше підвищення R_З/x₁ веде до зниження k_З. Очевидно, що при  коротке замикання відсутнє і k_З=1.

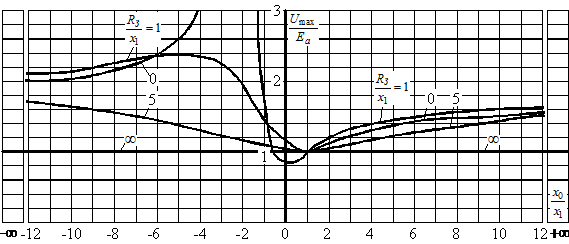
Рисунок 3.6 – Криві залежності максимальної напруги на здорових фазах від відношення x₀/x₁ для різних R₃/ x₁ при однофазному короткому замиканні,