1.10.4 Критерії оцінки надійності програмних засобів.
Всі існуючі показники надійності програмних засобів можна розбити на дві великі групи:
а) кількісні показники надійності ПЗ;
б) якісні показники надійності ПЗ.
Не розглядаючи якісні характеристики надійності, які достатньо детально досліджені в [11 – 13], зупинимося детальніше на можливості використання кількісних показників для оцінки і прогнозування надійності ПЗ.
Найзручніше як кількісні показники використовувати статистичні (ймовірнісні) критерії добре розробленої теорії надійності електронної апаратури. Слід враховувати, що оцінювання надійності ПЗ на основі статистичної теорії надійності апаратури можливе в межах деяких обмежень, що враховують специфіку ПЗ як певного виду продукту людської праці.
Можна виділити такі характеристики і кількісні показники надійності ПЗ:
1. Безвідмовність. Кажучи про безвідмовність ПЗ, що характеризує здатність ПЗ виконувати задані функції в заданих умовах експлуатації ТЗ, вважатимемо, що відмова програми – це результат прояву прихованої помилки. Слід мати на увазі, що вхідні дані і дані, створювані програмою, не є елементами ПЗ, оскільки їх надійність пов'язана з роботою зовнішніх пристроїв і апаратної частини ТЗ. Тільки константи, що вводяться програмістом, вважаються частиною ПЗ.
Для невідновлюваних в ході експлуатації програм узагальненою характеристикою надійності (безвідмовності) є вірогідність безвідмовної роботи P(t), яка характеризує вірогідність того, що за час t відмови не відбудеться:
P(t) = P(T ≥ t) = 1 – q(t), (1.151)
де T – час роботи ПЗ до відмови або напрацювання ПЗ до відмови (T – випадкова величина);
q(t) – вірогідність відмови ПЗ.
З (1.151) можна визначити функцію інтенсивності відмов ПЗ за формулою
. (1.152)
Середній час напрацювання до настання відмови (середній час безвідмовної роботи) визначається як математичне сподівання часового інтервалу між двома послідовними порушеннями роботоздатності ПЗ:
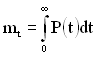. (1.153)
Для експоненційного закону розподілу відмов:
; 
. (1.154)
Оскільки програми мають явно виражені виробничі цикли роботи, то напрацювання програми може бути виражене або через календарний час, або через машинний час, або через кількість відпрацьованих операторів, вирішених задач та ін.
Один із способів оцінювання 
- спостереження за поведінкою програми у певний часовий період. Тоді величину середнього часу між відмовами (збоями) ПЗ можна визначити так:
, (1.155)
де n – загальна кількість прогонів ПЗ;
r – кількість прогонів ПЗ без помилок;
H – загальна кількість годин успішного прогону програми, що визначається за формулою:
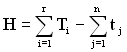, (1.156)
де 
– час безперервного прогону в годинах безпомилкової роботи ПЗ;
tj – час прогону в годинах до прояви помилки ПЗ;
k = n – r – кількість прогонів з помилками.
Вважаючи кількість помилок постійним, можна обчислити інтенсивність відмов ПЗ, зведену до однієї години роботи 
, і середній час між сусідніми відмовами ПЗ:
; (1.157)
. (1.158)
Класифікуючи відмови ПЗ за видами відмов – апаратні, програмні, оператора та ін. можна визначити частинні (зважені) інтенсивності відмов за відповідними видами помилок – 
, 
, 
та ін., а загальна надійність визначається як сума цих інтенсивностей. Такий підхід може значно полегшити збір статистичних даних відповіднх видів відмов на основі незалежного аналізу програмних засобів різних типів.
У випадку, якщо в ході експлуатації можливе коректування ПЗ або відновлення програми після відмови, викликаної дією перешкод (збоїв) від непрограмних джерел, а час відновлення достатньо малий порівняно з часом між відмовами чи збоями, то узагальненою характеристикою безвідмовності ПЗ є інтенсивність потоку відмов в часі ω(t):
; (1.159)
, (1.160)
де H(t) – середнє число відмов за час t;
– середній час напрацювання між двома відмовами.
Для програм, час коректування яких приблизно дорівнює часові між відмовами, узагальненою характеристикою безвідмовності є функція коефіцієнта готовності 
, залежного від часу. Показник готовності характеризує вірогідність застати ТЗ в заданий момент часу в роботоздатному стані.
2. Стійкість. Стійкість ПЗ визначає здатність ТЗ виконувати задані функції в умовах дії перешкод (помилок, збоїв, відмов), що виникають в непрограмних джерелах (технічне забезпечення, початкові дані). При оцінюванні стійкості ПЗ повинні бути задані параметри навколишнього середовища, по відношенню до якого оцінюється стійкість програм.
Показники стійкості – це показники безвідмовності, але з використанням умовних вірогідностей. Умовою, при якій обчислюється вірогідність, є відмова (збій) в програмі або апаратурі.
Для невідновлюваних (некоректовних) програм узагальненим показником стійкості служить умова вірогідності безвідмовної роботи:
, (1.161)
де P(A) – вірогідність помилки (збою) програми або відмови апаратури.
Безвідмовність і стійкість – динамічні характеристики, тобто вони характеризують надійність ПЗ в процесі його роботи.
3. Коректовність. Цей показник надійності ПЗ аналогічний до показника ремонтопридатності ТЗ, він характеризує пристосованість ПЗ до пошуку і усунення помилок і внесення в нього змін в ході експлуатації. Він використовується для характеристики відновлюваних в ході експлуатації програм. Показники коректовності: час коректування 
, вірогідність коректування програми за заданий час 
, коефіцієнт готовності Кг, параметр потоку коректувань 
.
4. Захищеність і довговічність. Додатковими характеристиками надійності ПЗ є показник захищеності від сторонніх втручань в роботу ПЗ і
показник довговічності, що характеризує властивості програм уникати морального старіння при тривалому використанні. Захищеність характеризується вірогідністю внесення спотворень при сторонньому втручанні, а довговічність – часом відмови ПЗ унаслідок морального старіння.
Залежно від умов застосування ПЗ можна виділити три режими його роботи:
а) програма не коректується, і будь-яка відмова є повною, тобто після відмови ПЗ не відновлюється. Основні показники надійності для цього режиму роботи програм – безвідмовність, стійкість (firmness) і захищеність (protected);
б) програма не коректується, проте після відмови ПЗ технічний засіб продовжує функціонувати правильно. Основні показники надійності – безвідмовність, стійкість, захищеність і довговічність;
в) після кожної відмови ПЗ коректується, відлагоджується і лише після цього знову здається в експлуатацію. Основні показники надійності – безвідмовність, стійкість, коректуємість, захищеність, а також втрати часу.
1.10.5 Математичні моделі надійності комплексів програм
Математичні моделі дозволяють оцінювати характеристики помилок в програмах і прогнозувати їх надійність при проектуванні і експлуатації. Моделі мають ймовірнісний характер, і достовірність прогнозів залежить від точності початкових даних і глибини прогнозування за часом. Ці математичні моделі призначені для оцінки:
- показників надійності комплексів програм в процесі відлагодження;
- кількості помилок, що залишилися невиявленими;
- часу, необхідного для виявлення наступної помилки в функціонуючій програмі;
- часу, необхідного для виявлення всіх помилок із заданою вірогідністю.
Використання моделей дозволяє ефективно і цілеспрямовано проводити відлагодження і випробування комплексів програм, допомагає приймати раціональне рішення про час припинення налагоджувальних робіт.
В даний час запропонований ряд математичних моделей, основними з яких є:
- експоненціальна модель зміни помилок залежно від часу відлагодження;
- модель, що враховує дискретно понижувальну частоту появи помилок як лінійну функцію часу тестування і випробувань;
- модель, що базується на розподілі Вейбулла;
- модель, заснована на дискретному гіпергеометричному розподілі.
При обґрунтуванні математичних моделей висуваються деякі гіпотези про характер проявів помилок в комплексі програм. Найбільш обґрунтованими є припущення, на яких базується перша експоненціальна модель зміни помилок в процесі відлагодження і які полягають в такому:
а) будь-які помилки в програмі є незалежними і виявляються у випадкові моменти часу;
б) час роботи між помилками визначається середнім часом виконання команди на ЕОМ і середнім числом команд, що виконуються між помилками. Це означає, що інтенсивність прояву помилок при реальному функціонуванні програми залежить від середньої швидкодії ЕОМ;
в) помилка, що є причиною спотворення результатів, фіксується і виправляється після завершення тестування або взагалі не виявляється.
З цих властивостей виходить, що за нормальних умов експлуатації кількість помилок, що виявляються в деякому інтервалі часу, розподілені за законом Пуассона. А тривалість безперервної роботи між спотвореннями розподілена експоненціально.
Припустимо, що на початку відлагодження комплексу програм при
τ = 0 в ній містилося 
помилок. Після відлагодження за інтервал часу
τ залишилося 
помилок і усунено n помилок 
. При цьому час
τ відповідає тривалості виконання програм на обчислювальному засобі для виявлення помилок і не враховує простоїв ТЗ, необхідних для аналізування результатів і проведення коректувань.
Інтенсивність виявлення помилок в програмі dn/dτ і абсолютна кількість усунених помилок пов'язані рівнянням:
, (1.162)
де b – коефіцієнт пропорційності.
Якщо припустити, що на початку відлагодження при τ = 0 помилки відсутні, то розв’язок рівняння (1.162) має вигляд:
. (1.163)
Кількість помилок, що залишилися, в комплексі програм
,
пропорційна інтенсивності виявлення dn/dτ з точністю до коефіцієнта b.
Час безвідмовної роботи програм до відмови T або напрацювання на відмову, який розглядається як знайдене спотворення програм, даних чи обчислювального процесу, що порушують роботоздатність, дорівнює величині, зворотній інтенсивності виявлення відмов (помилок):
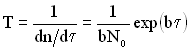. (1.164)
Якщо врахувати, що до початку тестування в комплексі програм містилося 
помилок і цьому відповідало напрацювання до відмови Т0, то функцію напрацювання до відмови від тривалості перевірок можна записати в такому вигляді:
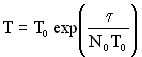. (1.165)
Якщо відомі моменти виявлення помилок 
і кожного разу в ці моменти виявляється і достовірно усувається одна помилка, то, використовуючи метод максимальної правдоподібності, можна отримати рівняння для визначення значення початкової кількості помилок 
:
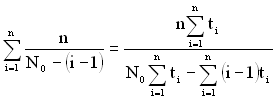, (1.166)
а також вираз для розрахунку коефіцієнта пропорційності
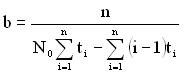. (1.167)
В результаті можна розрахувати кількість помилок, що залишилися в програмі, і середнє напрацювання до відмови 
, тобто отримати оцінку часу до виявлення наступної помилки.
В процесі відлагодження і випробувань програм для підвищення напрацювання до відмови від 
до 
необхідно виявити і усунути
Δn помилок. Величина
Δn визначається співвідношенням:
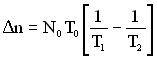. (1.168)
Вираз для визначення затрат часу
Δτ на проведення відлагодження, що дозволяє усунути
Δn помилок і відповідно підвищити напрацювання до відмови від значення 
до 
має вигляд:
. (1.169)
Друга модель побудована на основі гіпотези про те, що частота прояву помилок (інтенсивність відмов) лінійно залежить від часу випробування 
між моментами виявлення послідовних i-ої та (i - 1)-ої помилок:
, (1.170)
де 
– початкова кількість помилок;
b – коефіцієнт пропорційності, що забезпечує рівність одиниці площі під кривою вірогідності виявлення помилок.
Для оцінки напрацювання до відмови виходить вираз, який відповідає розподілу Релея:
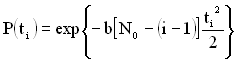, (1.171)
де
.
З урахуванням рівняння (1.171) щільність розподілу часу напрацювання до відмови описується виразом:
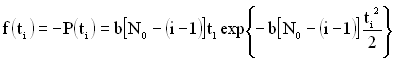. (1.172)
Використавши функцію максимальної правдоподібності, отримаємо оцінку для загальної кількості помилок 
і коефіцієнта b:
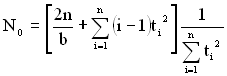; (1.173)
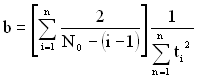. (1.174)
Особливістю третьої моделі є облік ступінчастого характеру зміни надійності при усуненні чергової помилки. Як головна розглядається функція розподілу часу напрацювання до відмови P(t). Якщо помилки не усуваються, то інтенсивність відмов є постійною, що приводить до експоненціальної моделі розподілу:
.
Звідси щільність розподілу напрацювання до відмови T визначається за виразом:
,
де t > 0,
λ > 0 і 1/λ – середній час напрацювання до відмови, тобто 
.
Для апроксимації зміни інтенсивності від часу при виявленні і усуненні помилок використовується функція такого вигляду:
.
Якщо 0 < β < 1, то інтенсивність відмов знижується при налагодженні або в процесі експлуатації. При такому вигляді функції λ(t) щільність функції розподілу напрацювання до відмови описується двопараметричним розподілом Вейбулла:
.
Розподіл Вейбулла досить добре відображає реальні залежності при розрахунку функції напрацювання до відмови.
Питання для самоконтролю
1. Дайте означення надійності та основних властивостей надійності ТЗ.
2. Перерахуйте основні терміни, що використовуються в теорії надійності відповідно до ГОСТу.
3. Перерахуйте основні показники метрологічної надійності засобів вимірювальної техніки.
4. Перерахуйте основні показники надійності невідновлюваних ТЗ.
5. Які показники надійності відновлюваних ТЗ найчастіше нормуються?
6. Наведіть вираз, за яким розраховується середнє напрацювання до першої відмови.
7. Наведіть вирази для визначення статистичних оцінок показників надійності невідновлюваних ТЗ.
8. Наведіть вирази, за якими розраховуються ймовірнісні оцінки коефіцієнта готовності та коефіцієнта вимушеного простою.
9. В чому основні відмінності показників довговічності і збережності?
10. Наведіть методику нормування показників метрологічної надійності.
11. Які характеристики надійності спільні, а які відмінні між програмними і апаратними показниками надійності?
12. Перерахуйте основні проблем дослідження надійності програмного забезпечення.
13. Які Ви знаєте кількісні показники надійності програмного забезпечення?
14. Наведіть математичні моделі для оцінювання надійності комплексів програм.
15. Як розраховується середній час до першої відмови при оцінюванні показників метрологічної надійності?
16. Як розраховують вірогідність безвідмовної роботи при оцінюванні показників метрологічної надійності?
17. Наведіть аналітичний вираз для визначення функції інтенсивності відмов програмного забезпечення.
18. За якою формулою розраховується загальна кількість годин успішного прогону програми?
