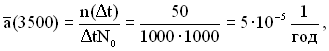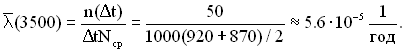1.2 Показники надійності невідновлюваних ТЗ
Основними нормованими показниками надійності невідновлюваних ТЗ можуть бути такі показники:
– ймовірність безвідмовної роботи (probability of faultless work) P(t);
– ймовірність відмови (probability of refuse) Q(t);
– частота відмов (frequency of refuses) a(t);
– інтенсивність відмов (intensity of refuses) λ(t);
– середнє напрацювання (middle work) до першої відмови Tср.
Оскільки час настання відмови T є величина випадкова, то Q(t) – це ймовірність того, що випадкова величина Т набуде значення, менше або рівне t (інтегральна функція (integral function) розподілу відмов), де t – час, за який визначається показник надійності (reliability index), тобто ймовірністю відмови називається ймовірність того, що за певних умов експлуатації в заданому інтервалі часу виникне хоча б одна відмова
![]() . (1.1)
. (1.1)
Ймовірністю безвідмовної роботи P(t) називається ймовірність того, що за певних умов експлуатації в заданому інтервалі часу або у межах заданого напрацювання t не відбудеться жодної відмови
![]() . (1.2)
. (1.2)
Оскільки безвідмовна робота (faultless work) і відмова є подіями неспільними і протилежними, то між ними справедливе таке співвідношення
![]() . (1.3)
. (1.3)
Оскільки Q(t) є законом розподілу випадкової величини (відмов), то залежність між можливими значеннями безперервної випадкової величини T та ймовірностями влучення в їх межі називається щільністю ймовірності (closeness of probability).
Вважаючи, що в момент ввімкнення ТЗ роботоздатний, тобто Р(0) = = 1, функція Р(t) монотонно спадає від 1 до 0 так, як це показано на рис. 1.1. При цьому абсолютно зрозумілим є те, що Р(![]() )=0, тобто будь-який ТЗ при
)=0, тобто будь-який ТЗ при ![]() з часом відмовить.
з часом відмовить.
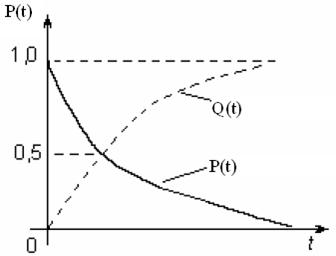
Рисунок 1.1 – Характеристики зміни ймовірності безвідмовної роботи та ймовірності відмови
Частота відмов a(t) є щільністю ймовірності часу роботи ТЗ до першої відмови
![]() (1.4)
(1.4)
Інтенсивністю відмов називається відношення числа відмовлених ТЗ за одиницю часу до середнього числа ТЗ, що справно працюють в даному проміжку часу. Ймовірнісна оцінка цієї характеристики знаходиться за виразом
![]() . (1.5)
. (1.5)
Середнім напрацюванням до першої відмови Tср називається математичне сподівання (момент першого порядку) M[t] часу роботи ТЗ до відмови. Математичне сподівання, тобто ![]() , обчислюється за частотою відмов (щільність розподілу часу безвідмовної роботи) так
, обчислюється за частотою відмов (щільність розподілу часу безвідмовної роботи) так
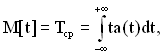 (1.6)
(1.6)
оскільки ![]() і
і ![]() , а
, а ![]() , то
, то 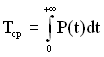 .
.
Величина Тср – параметр функції Р(t), який в багатьох випадках дозволяє відновити всю функцію.
Інколи середній час безвідмовної роботи Тср є прийнятною характеристикою для порівняння ТЗ за показниками безвідмовності.
Знаючи один з показників надійності і закон розподілу відмов, можна обчислити інші характеристики надійності, враховуючи такі формули:
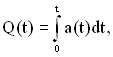 (1.7)
(1.7)
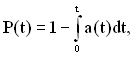 (1.8)
(1.8)
![]() , (1.9)
, (1.9)
де ![]() – інтенсивність відмов, що розраховується за формулою (1.5).
– інтенсивність відмов, що розраховується за формулою (1.5).
Момент другого порядку розраховується за формулою
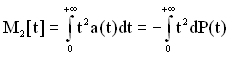 . (1.10)
. (1.10)
З врахуванням того, що Р(t)=1 при t=0, а ![]() , остаточно отримаємо
, остаточно отримаємо
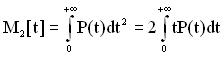 . (1.11)
. (1.11)
З виразу (1.11) із врахуванням (1.6) можна знайди дисперсію часу ![]() безвідмовної роботи ТЗ за формулою
безвідмовної роботи ТЗ за формулою
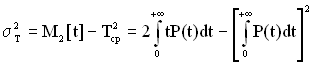 . (1.12)
. (1.12)
Приклад 1.1. Інтенсивність відмов ТЗ залежить від часу і виражається функцією ![]() . Необхідно визначити ймовірність безвідмовної роботи, частоту відмов і середнє напрацювання до першої відмови.
. Необхідно визначити ймовірність безвідмовної роботи, частоту відмов і середнє напрацювання до першої відмови.
Розв’язування:
Ймовірність безвідмовної роботи розрахуємо за формулою (1.9). Вона після відповідних математичних перетворень набуде вигляду: ![]() .
.
Частота відмов визначається шляхом підстановки Р(t) у формулу (1.5), яка після перетворень набуде вигляду: ![]() .
.
Відповідно до формули (1.6) середнє напрацювання до першої відмови буде дорівнювати: ![]() .
.
Статистичні оцінки (statistical estimations) показників надійності невідновлюваних ТЗ розраховуються за такими формулами.
Статистична оцінка ймовірності відмови визначається за формулою
![]() , (1.13)
, (1.13)
де ![]() – кількість ТЗ, що відмовили за час t;
– кількість ТЗ, що відмовили за час t;
![]() – загальна кількість ТЗ, що підлягають випробуванням.
– загальна кількість ТЗ, що підлягають випробуванням.
Статистична оцінка ймовірності безвідмовної роботи буде дорівнювати
![]() . (1.14)
. (1.14)
Статистична оцінка частоти відмов
![]() , (1.15)
, (1.15)
де ![]() – кількість ТЗ, що відмовили в інтервалі часу від
– кількість ТЗ, що відмовили в інтервалі часу від ![]() до
до ![]() ;
;
![]() – інтервал часу;
– інтервал часу;
![]() – час початку і-го інтервалу;
– час початку і-го інтервалу;
![]() – час кінця і-го інтервалу.
– час кінця і-го інтервалу.
Статистична оцінка інтенсивності відмов
![]() , (1.16)
, (1.16)
де ![]() – середня кількість відремонтованих ТЗ, що працюють в інтервалі часу
– середня кількість відремонтованих ТЗ, що працюють в інтервалі часу ![]() ;
;
![]() – кількість відремонтованих ТЗ, що працюють на початку інтервалу
– кількість відремонтованих ТЗ, що працюють на початку інтервалу ![]() ;
;
![]() – кількість ТЗ, що працюють в кінці інтервалу
– кількість ТЗ, що працюють в кінці інтервалу ![]() .
.
Знаючи моменти виходу з ладу всіх ТЗ, за якими ведеться спостереження, можна дати статистичну оцінку середнього напрацювання до першої відмови
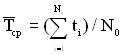 , (1.17)
, (1.17)
де ![]() – час безвідмовної роботи i-го зразка ТЗ.
– час безвідмовної роботи i-го зразка ТЗ.
Маючи дані про кількість ТЗ, що вийшли з ладу в кожному i-тому інтервалі часу, статистичну оцінку середнього напрацювання до першої відмови можна визначити з рівняння
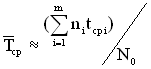 , (1.18)
, (1.18)
де ![]()
![]() ;
;
![]() – час початку і-го інтервалу,
– час початку і-го інтервалу, ![]() - час кінця і-го інтервалу;
- час кінця і-го інтервалу;
![]() – час, протягом якого вийшли із ладу всі ТЗ;
– час, протягом якого вийшли із ладу всі ТЗ;
![]() – інтервал часу.
– інтервал часу.
Приклад 1.2. На випробування направлено 1000 ТЗ. За 3000 год. відмовило 80 ТЗ, а за інтервал часу 3000 ÷ 4000 год. відмовило ще 50 ТЗ. Необхідно визначити ймовірність безвідмовної роботи та ймовірність відмови протягом 3000 год.; частоту та інтенсивність відмови у проміжку часу 3000 ÷ 4000 год.
Розв’язування:
За формулами (1.13) і (1.14) визначаємо:
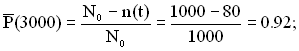
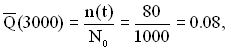 або
або ![]()
За формулами (1.15) і (1.16) знаходимо оцінку частоти та інтенсивності відмов: