2.5 Гамма-розподіл

 

 

При гамма-розподілі щільність розподілу напрацювання до відмови описується виразом

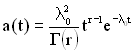, (2.18)

де Г(r) – повна гамма-функція.

В теорії надійності гамма-розподіл, як правило, використовується при цілому значенні параметра r. Якщо r = 1, то гамма-розподіл пере-творюється в експоненційний розподіл. Якщо r – ціле число більше 1, то гамма-розподіл є розподілом суми незалежних випадкових величин, кожна з яких має експоненційний розподіл.

Гамма-розподіл при цілому значенні r інколи називають розподілом Ерланга. Для такого розподілу ймовірність безвідмовної роботи на інтервалі (0; t) описується виразом (рис. 2.6, а):

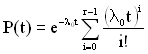. (2.19)

Щільність розподілу напрацювання до відмови в цьому випадку описується виразом (рис. 2.6, б)

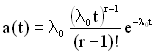. (2.20)

Інтенсивність відмов визначається за формулою (2.6, в)

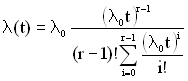. (2.21)

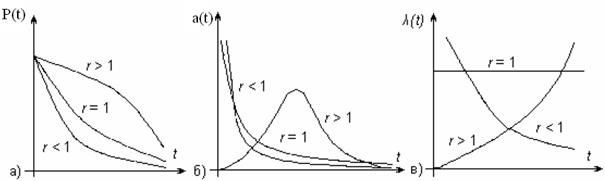
Рисунок 2.6 – Характеристики зміни гамма-розподілу: а) – функція надійності; б) – щільність розподілу напрацювання до відмови; в) – інтенсивність відмов

Середній час безвідмовної роботи і дисперсія часу безвідмовної роботи відповідно описуються виразами:

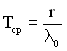, (2.22)

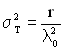. (2.23)

При великих значеннях параметра r – гамма-розподіл наближається до нормального закону розподілу з параметрами: , .

Прикладом використання гамма-розподілу є резервна система, що складається з r однакових елементів. При цьому під навантаженням знаходиться один елемент. Інші елементи почергово автоматично вмикаються в роботу після відмови працюючого елемента. При експоненційному напрацюванні до відмови елементів їх сумарне напрацювання буде підпорядковуватися гамма-розподілу.

 

2.6 Нормальний розподіл

 

Нормальний закон розподілу (normal law of distributing) – це двопараметричний закон з параметрами розподілу: – математичне

сподівання і Т – СКВ (час безвідмовної роботи).

Ймовірність події в інтервалі часу від до визначається за формулою

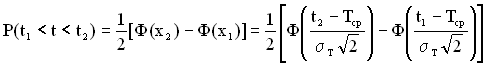, (2.24)

де – інтеграл ймовірності (інтеграл Лапласа) виду

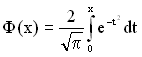. (2.25)

При використанні центрованої і нормованої функції Лапласа , де , ймовірність безвідмовної роботи визначається за формулою

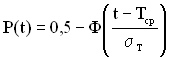. (2.26)

Щільність розподілу напрацювання до відмови при нормальному розподілі має вигляд (рис. 2.7)

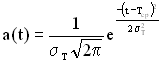. (2.27)

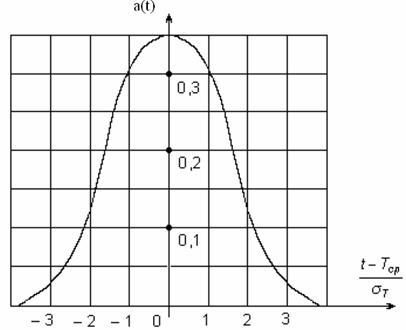
Рисунок 2.7 – Щільність розподілу напрацювання до відмови

для нормального закону розподілу

Функцію надійності з врахуванням виразу (2.27) можна також записати у вигляді

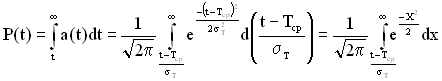, (2.28)

де Х=.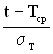

Ймовірність відмови на інтервалі (0; t) (функція ненадійності) визначається за формулою

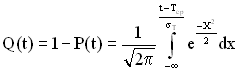. (2.29)

 

2.7 Трикутний розподіл

 

Цей розподіл характеризує обмежену область значень випадкових величин (tН; tВ), де tН і tВ – межі області можливих значень випадкових величин.

Розглянемо показники надійності трикутного розподілу:

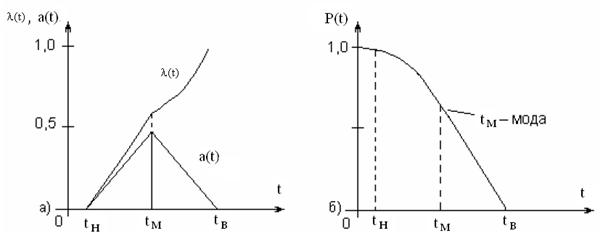
  •   характеристики зміни щільності а(t) та інтенсивності відмов (рис. 2.8, а);
  •  характеристики зміни функції надійності Р(t) (рис. 2.8, б).

    Рисунок 2.8 – Характеристики зміни показників надійності при трикутному розподілі відмов

    Позначимо значення щільності розподілу в точці моди через а(tM)=h, тоді h(tВ – tM)/2=1.

    В цьому випадку щільність розподілу можна записати у вигляді таких формул:

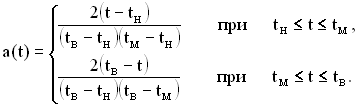    (2.30)

    Функція надійності Р(t) буде описуватись такою системою рівнянь:

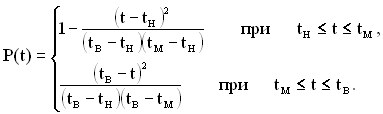    (2.31)

    Інтенсивність відмов при цьому буде дорівнювати:

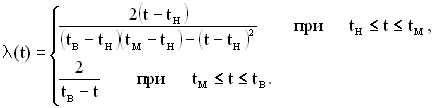    (2.32)

    Середній час напрацювання до відмови Тср визначається за формулою

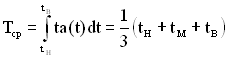    . (2.33)

     

    2.8 Закони розподілу дискретних випадкових величин

     

    Наведені вище розподіли характеризують неперервні випадкові величини, наприклад, час безвідмовної роботи або час відновлення.

    Але в ряді випадків при розрахунку надійності ТЗ виникає необхідність оцінки дискретних випадкових величин, наприклад, кількості відмов протягом заданого інтервалу часу.

    Тому розглянемо найбільш часто використовувані при розрахунках надійності розподіли дискретних випадкових величин.

     

    2.8.1 Біноміальний розподіл.

     

    Для такого розподілу можливі значення випадкової величини 0, 1, 2, 3, …, n.

    Ймовірність появи m сприятливих подій із загальної кількості n подій дорівнює

    . (2.34)

    Математичне сподівання і дисперсія відповідно будуть дорівнювати:

    , (2.35)

    , (2.36)

    де Р – ймовірність здійснення події при одноразовому випробуванні;

    Q = 1 – Р.

     

    2.8.2 Розподіл Пуассона.

     

    Можливі значення випадкової величини для такого розподілу такі: 0, 1, 2, …, n. Ймовірність появи m подій дорівнює

    . (2.37)

    Математичне сподівання і дисперсія відповідно будуть дорівнювати:

    , (2.38)

    , (2.39)

    де – параметр розподілення.

        

    2.8.3 Геометричний розподіл.

     

    Можливі значення випадкової величини такі: 0, 1, 2, …, n. Ймовірність появи m подій дорівнює

    . (2.40)

    Математичне сподівання і дисперсія відповідно будуть дорівнювати:

    , (2.41)

    , (2.42)

    де Р – ймовірність появи події при одноразовому випробуванні;

    Q = 1 – Р.

     

    Питання для самоконтролю

     

    1.  Проаналізуйте три «періоди життя» ТЗ.

    2. Перерахуйте основні розподіли дискретних випадкових величин, що використовуються для розрахунку показників надійності.

    3. Наведіть приклади використання гамма-розподілу неперервних випадкових величин.

    4. Яким законам розподілу відповідають «періоди життя» ТЗ?

    5. Наведіть аналітичні вирази для розрахунку основних показників надійності, що підпорядковуються розподілу Вейбулла.

    6. Наведіть вирази для розрахунку середнього напрацювання до відмови та дисперсії часу безвідмовної роботи при експоненційному розподілі відмов.

    		•