Розділ 4 ЗАГАЛЬНІ МЕТОДИ РОЗРАХУНКУ НАДІЙНОСТІ ПРОЕКТОВНИХ ТЕХНІЧНИХ ЗАСОБІВ РІЗНИХ ТИПІВ
4.1 Способи і основні етапи визначення надійності проектовних технічних засобів
Якщо існують відомості про надійність елементів ТЗ і зв'язки між елементами, то за цими даними можна визначити значення показників надійності ТЗ.
Визначення надійності ТЗ або системи в цілому переслідує такі цілі:
1. Визначити, чи досяжна задана надійність на сучасному рівні розвитку техніки;
2. Допомогти розподілити значення показників надійності (ПН) за елементами, блоками і вузлами;
3. Допомогти зробити вибір між різними конструктивними рішеннями;
4. Установити доцільність введення резервування.
Існує два шляхи визначення надійності ТЗ:
Загальноприйнятим на сьогоднішній день є перший шлях. Тут необхідно визначити, які стани ТЗ треба враховувати, ознаки цих станів і ін., тобто необхідно описати функціонування реального ТЗ формальною мовою подій і станів.
Найбільшого поширення одержали логічні моделі безвідмовної роботи ТЗ. При цьому вважають , що елементи можуть знаходитися в двох несумісних станах: роботоздатному і нероботоздатному. Функціональні зв'язки між елементами заміняються логічними, які характеризують стан ТЗ. Умови роботоздатності ТЗ при відмові елементів записуються за допомогою логічних співвідношень.
Вигляд логічної моделі визначає можливість одержання розрахункових формул. Для опису надійності найбільшого поширення отримали такі методи:
- метод інтегральних рівнянь;
- метод диференційних рівнянь;
- метод оцінки надійності за графом можливих станів ТЗ.
4.2 Метод інтегральних рівнянь
Цей метод можна застосовувати при розрахунку надійності будь-яких ТЗ при будь-яких розподілах часу безвідмовної роботи і часу відновлення.
Визначення ПН в цьому методі відбувається шляхом складання і вирішення інтегральних або інтеграло-диференційних рівнянь. При складанні інтегральних рівнянь звичайно виділяють нескінченно малі інтервали часу. Для цих інтервалів часу розглядають складні події, що з'являються при спільній дії декількох факторів.
Ці рівняння порівняно просто складати, але важко розв’язати. Часто розв’язок доводиться знаходити чисельними методами за допомогою ЕОМ. У зв'язку з цим метод інтегральних рівнянь у даний час не одержав широкого розповсюдження.
Як приклад застосування цього методу розглянемо розрахунок надійності невідновлюваного ТЗ із холодним резервом.
При цьому припустимо:
- індикатор відмов і перемикач абсолютно надійні;
- резервні елементи не можуть відмовити до включення їх в роботу;
- ремонт резервного ТЗ в процесі його роботи неможливий.
Такий резервований ТЗ буде безвідмовно працювати протягом часу (0; t) при двох можливих подіях:
- основний елемент не відмовив;
- основний елемент відмовив у момент ![]() , а резервний елемент проробив безвідмовно протягом інтервалу
, а резервний елемент проробив безвідмовно протягом інтервалу ![]() .
.
Позначимо ймовірність першої події ![]() . Очевидно, що ймовірність появи відмови основного елемента протягом малого інтервалу часу
. Очевидно, що ймовірність появи відмови основного елемента протягом малого інтервалу часу ![]() дорівнює:
дорівнює:
![]() , (4.1)
, (4.1)
де ![]() – щільність ймовірності моменту і-ої відмови.
– щільність ймовірності моменту і-ої відмови.
Ймовірність безвідмовної роботи ТЗ за умови, що в момент ![]() відбулася відмова основного елемента і включився резервний, дорівнює:
відбулася відмова основного елемента і включився резервний, дорівнює:
![]() . (4.2)
. (4.2)
Таким чином, ймовірність здійснення другої події на інтервалі ![]() дорівнює
дорівнює
![]() . (4.3)
. (4.3)
Інтегруючи вираз (4.3) від 0 до t, одержимо ймовірність здійснення другої події
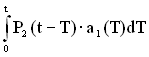 . (4.4)
. (4.4)
Очевидно, що ймовірність дубльованого ТЗ з холодним резервом дорівнює сумі ймовірностей здійснення першої і другої подій
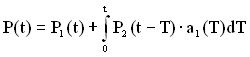 . (4.5)
. (4.5)
При показовому розподілі напрацювання до відмови основного і резервного елементів, що мають інтенсивність відмов ![]() і
і ![]() з виразу (4.5) маємо:
з виразу (4.5) маємо:
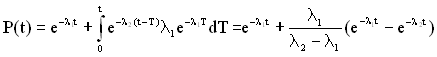 . (4.6)
. (4.6)
Щільність напрацювання такого ТЗ до відмови визначається за формулою
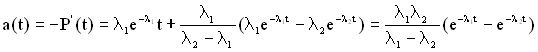 . (4.7)
. (4.7)
Якщо ТЗ має один основний і (K–1) резервний елемент, то, взявши
за основу вираз (4.5) можна отримати рекурентну формулу
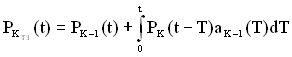 , (4.8)
, (4.8)
де індекс (K–1) – означає, що відповідні характеристики належать до резервного ТЗ, при відмові якого включається в роботу останній, K-й, резервний елемент.
4.3 Метод диференційних рівнянь
Цей метод заснований на припущенні того, що час між відмовами і час відновлення підлягають показниковим розподілам.
При цьому параметр потоку відмов
Ω=![]() , а інтенсивність віднови
, а інтенсивність віднови ![]() , де
, де ![]() ,
, ![]() – відповідно середній час до відмови і час відновлення.
– відповідно середній час до відмови і час відновлення.
Цей метод може застосовуватися для розрахунку надійності як відновлюваних, так і невідновлюваних ТЗ. Для використання цього методу необхідно мати математичну модель у вигляді множини станів ТЗ, в яких він може знаходитися при відмовах та відновленнях.
Для визначення ПН складають і розв’язують систему диференційних рівнянь для ймовірностей станів (рівнянь Колмогорова). Щоб при цьому гранично зменшити витрати праці на розрахунок зазвичай припускають, що:
- об'єкти, що відмовили, починають негайно відновлювати;
- відсутні обмеження на кількість відновлень;
- надійність засобів контролю ідеальна.
Математичну модель зображують у вигляді графа станів. На цьому графі кружечками зображують можливі стани ТЗ при відмовах її елементів. Стрілками зображують можливі напрямки переходів ТЗ з одного стану в інший. Біля стрілок вказують інтенсивність переходів (наприклад, ![]() і
і ![]() ).
).
Зобразимо приклад такого графа на рис. 4.1.
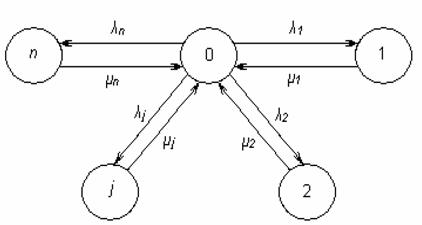
Рисунок 4.1 – Граф станів відновлюваного ТЗ
Якщо розглядається невідновлюваний ТЗ, то між станами є тільки одна стрілка.
Для визначення ймовірностей ![]() перебування ТЗ в
перебування ТЗ в ![]() -му стані в момент часу
-му стані в момент часу ![]() складають за графом станів систему звичайних диференційних рівнянь.
складають за графом станів систему звичайних диференційних рівнянь.
Для цього в ліву частину кожного рівняння ставлять похідну за часом від ймовірності перебування ТЗ в ![]() -му стані в момент часу
-му стані в момент часу ![]() . Кількість членів у правій частині дорівнює кількості стрілок, що з'єднують розглянутий стан з іншим. При цьому кожен член дорівнює ймовірності переходу з одного стану в інший, а саме добуткові інтенсивності переходу (наприклад,
. Кількість членів у правій частині дорівнює кількості стрілок, що з'єднують розглянутий стан з іншим. При цьому кожен член дорівнює ймовірності переходу з одного стану в інший, а саме добуткові інтенсивності переходу (наприклад, ![]() ) на ймовірність того i-го стану, з якого стрілка виходить. Знак добутку береться додатним, коли стрілка входить у розглянутий стан.
) на ймовірність того i-го стану, з якого стрілка виходить. Знак добутку береться додатним, коли стрілка входить у розглянутий стан.
Отримана система диференційних рівнянь доповнюється нормованою умовою
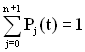 , (4.9)
, (4.9)
де ![]() – ймовірність перебування ТЗ в j-му стані;
– ймовірність перебування ТЗ в j-му стані;
![]() – кількість можливих станів.
– кількість можливих станів.
Далі вся множина станів розбивається на дві підмножини:
а) ![]() – підмножина станів, у якому ТЗ нероботоздатний;
– підмножина станів, у якому ТЗ нероботоздатний;
б) ![]() – підмножина станів, у яких ТЗ роботоздатний.
– підмножина станів, у яких ТЗ роботоздатний.
Тоді функцію готовності ТЗ можна визначити як
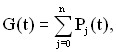 (4.10)
(4.10)
де ![]() – ймовірність перебування ТЗ в j-му роботоздатному стані.
– ймовірність перебування ТЗ в j-му роботоздатному стані.
Якщо необхідно визначити коефіцієнт готовності (або простою) розглядають сталий режим експлуатації при ![]() .
.
У цьому випадку всі похідні ![]() і система диференційних рівнянь переходить у систему алгебраїчних рівнянь.
і система диференційних рівнянь переходить у систему алгебраїчних рівнянь.
Приклад 4.1. Обчислимо коефіцієнт готовності ТЗ, якщо коефіцієнт готовності кожного з n елементів ТЗ відповідно дорівнює: ![]()
Вважаємо, що весь ТЗ відмовляє, якщо відмовив хоча б один з його елементів.
Розв’язування:
Необхідно розглянути всі стани ТЗ. Для цього складається граф станів (див. рис. 4.1). Цей граф позначає такі стани ТЗ:
0 – всі елементи роботоздатні;
1 – перший елемент нероботоздатний, інші роботоздатні;
2 – другий елемент нероботоздатний, інші роботоздатні і т.д.
Ймовірність появи одночасно двох нероботоздатних елементів вважаємо настільки малою, що нею можна знехтувати.
Символами ![]() – позначені інтенсивності відмов, а символами
– позначені інтенсивності відмов, а символами ![]() – позначені інтенсивності відновлення.
– позначені інтенсивності відновлення.
За графом станів складаємо систему диференційних рівнянь:
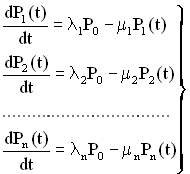 . (4.11)
. (4.11)
Сюди ж додають нормовану умову (4.9) 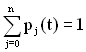 .
.
При сталому режимі експлуатації рівняння виду (4.11) набудуть вигляду:
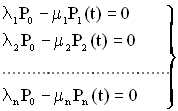 . (4.12)
. (4.12)
Розв’язавши отриману систему алгебраїчних рівнянь (4.12) з врахуванням нормованої умови, отримаємо
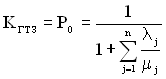 . (4.13)
. (4.13)
Ймовірність перебування ТЗ в j-му стані дорівнюватиме
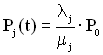 . (4.14)
. (4.14)
Знаючи формулу ![]() , маємо
, маємо
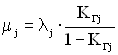 . (4.15)
. (4.15)
Підставивши в (4.13) вираз для ![]() з (4.15), отримаємо
з (4.15), отримаємо
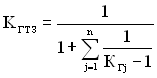 . (4.16)
. (4.16)
Нехай ![]() ;
; ![]() ;
;![]() .
.
Підставивши ці значення в (4.16), отримаємо коефіцієнт готовності ТЗ
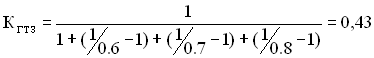 .
.