ЗМІСТ
1 Лабораторна робота №1. Множини. Основні поняття.
2 Лабораторна робота №2. Відношення.
3 Лабораторна робота №3. Алгоритми.
4 Лабораторна робота №4. Мінімізація логічних функцій методом діаграм Вейча.
5 Лабораторна робота №5. Основні поняття теорії графів.
6 Лабораторна робота №6. Матричні способи представлення графів.
7 Лабораторна робота №7. Пошук найкоротших шляхів у графах.
8 Лабораторна робота №8. Побудова найкоротших остов дерев графа.
9 Лабораторна робота №9. Розфарбування графа.
ЛАБОРАТОРНА РОБОТА №1. МНОЖИНИ. ОСНОВНІ ПОНЯТТЯ
Мета: Засвоїти основні поняття множин та способи їх задання.
Теоретичні відомості: Множини належать до категорії найзагальніших, основоположних понять математики.
Приклади:
• множина натуральних чисел;
• множина цифр десяткової системи;
• множина цифр двійкової системи;
• множина парних чисел.
Є кілька способів подання множин:
1. Вербальний (словесний) – за допомогою опису характеристичних властивостей, які повинні мати елементи множин. Об’єкти, що утворюють множину, називають її елементами, або членами. Прикладом множини можуть бути: множина сторінок книги (кожна сторінка є елементом цієї множини); множина всіх дійсних чисел, більших від ![]() і менших від 1; множина студентів тощо.
і менших від 1; множина студентів тощо.
2. Список (перелік) усіх елементів у фігурних дужках. Стосовно зазначених вище прикладів маємо:
{1, 2, 3, …};
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
{0, 1};
{2, 4, 6, …};
3. Предикатний (висловлювальний) за допомогою предиката, тобто множина подається у вигляді ![]() або
або ![]() , де P(x) є предикатом, набуває значення «істина» для елементів цієї множини. Приклади:
, де P(x) є предикатом, набуває значення «істина» для елементів цієї множини. Приклади:
{1, 2, 3, 4, …} = {x | x - натуральне число};
{0, 1, 2, 3, 4, …, 9} = {x | x – цифра десяткової системи числення};
{0, 1} = {x|x-цифра двійкової системи}= { x | x2 – x = 0};
{2, 4, 6, …} = { x| x – парне число} = { x | ![]() n
n ![]() N(x = 2n)};
N(x = 2n)};
4. За допомогою породжувальної процедури (алгоритму), що описує спосіб отримання елементів множини із уже існуючих елементів або інших об’єктів, якщо такий спосіб існує. Для зазначених прикладів існують породжувальні процедури. Для перших двох і четвертого це:
а) 1![]() ; б) якщо
; б) якщо ![]() , то
, то ![]() також є
також є ![]() ;
;
б) 0 ![]() ; б) якщо
; б) якщо ![]() ,то
,то ![]() також є
також є ![]() , доки
, доки ![]() ;
;
в) ![]() ; б) якщо
; б) якщо ![]() , то
, то ![]() , також є
, також є ![]() .
.
5. Аналітичний – за допомогою аналітичних виразів, що містять позначки множин та операцій над ними.
Із наведених прикладів випливає, що множини бувають скінченними та нескінченними. Множини називаються скінченними, якщо число їх елементів скінченне, тобто існує натуральне число n, яке є числом елементів множини. Множини називають нескінченними, якщо вони містять нескінченне число елементів.
Порожня множина
У теорії множин використовують поняття порожньої множини. Її позначають ![]() . Множина може взагалі не містити елементів, наприклад:
. Множина може взагалі не містити елементів, наприклад:
S = {x | x – непарне число, що ділиться на 2} = Ø ;
![]() ;
;
Для позначення цього факту вводять поняття порожньої множини. Це дає можливість оперувати будь-якою множиною без попереднього застереження, існує вона чи ні.
Операції над множинами
1. Об’єднання A і B (![]() ) – множина, що складається з усіх елементів множини А та всіх елементів В і не містить жодних інших елементів, тобто
) – множина, що складається з усіх елементів множини А та всіх елементів В і не містить жодних інших елементів, тобто ![]() , де символ «V» позначає логічну операцію диз’юнкції (логічне АБО), рис. 1.1.
, де символ «V» позначає логічну операцію диз’юнкції (логічне АБО), рис. 1.1.

2. Переріз А і В – множина, що складається з тих і тільки тих елементів, які належать одночасно множині А та множині В, тобто ![]() , де символ «
, де символ «![]() » позначає логічну операцію кон’юнкції (логічне І), рис.1.2.
» позначає логічну операцію кон’юнкції (логічне І), рис.1.2.
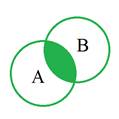
3. Різниця А та В (відносне доповнення) – множина, що складається з тих і тільки тих елементів, які належать множині А і не належать В, тобто
![]() , рис.1.3.
, рис.1.3.
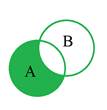
4. Диз’юнктивна сума А та В (симетрична різниця) – множина, що складається з усіх елементів А, які не належать множині В, й усіх елементів В, які не належать множині А, та яка не містить ніяких інших елементів, тобто ![]() , де для позначення операції диз’юнктивної суми двох множин використано той самий символ
, де для позначення операції диз’юнктивної суми двох множин використано той самий символ ![]() , що й для логічної операції додавання за mod2. Очевидно, що
, що й для логічної операції додавання за mod2. Очевидно, що ![]() – отже, остання формула є аналітичним поданням множин, рис.1.4.
– отже, остання формула є аналітичним поданням множин, рис.1.4.

Універсум V
Зручно сукупність допустимих об’єктів зафіксувати явно, та вважати, що множини, які розглядаються, складаються з елементів цієї сукупності. Її називають основною множиною (універсумом) і позначають через V.
Нова операція V – A = Ā (абсолютне доповнення).
Ā – це множина, що містить усі елементи універсуму, за винятком А, рис.1.5.

Множину, елементами якої є всі підмножини множини А, називають множиною підмножин (множиною-степенем) множини А і позначають P(A). Так, для триелементної множини ![]() маємо
маємо ![]() .
.
У разі скінченної множини A, що складається з n елементів, множина підмножин P(A) містить ![]() елементів [1].
елементів [1].
Завдання до лабораторної роботи
1. Складіть алгоритм та програму, який як вхідні дані одержує дві множини і визначає, чи рівні ці множини, чи є одна з них підмножиною другої.
2. Складіть алгоритм та програму, який як вхідні дані одержує множину і конструює список всіх можливих підмножин даної множини.
3. Складіть алгоритм та програму, яка моделює операції над множинами у графічному режимі:
![]() ;
;
![]() ;
;
![]() −B;
−B;
![]() .
.
Контрольні питання
1. Що таке множини? Наведіть приклади різних множин.
2. Як можна визначити множину?
3. У яких випадках можна вважати, що множина ![]() ,
, ![]() ,
, ![]() є рівними?
є рівними?
4. Що таке скінченна і нескінченна множини?
5. До яких із цих множин належить порожня множина?
6. Для чого використовують порожню множину?
7. Що таке підмножина?
8. Чи завжди будь-яка множина містить порожню множину? Аргументуйте відповідь.
9. Чим відрізняється за значенням строге включення ![]() від включення
від включення ![]() ? Аргументуйте відповідь.
? Аргументуйте відповідь.
10. Чим відрізняється поняття включення ![]() від поняття належності
від поняття належності ![]() ?
?
11. Як розрізняють елементи множини та її підмножини? Відповідь ілюструйте прикладами.
12. Що таке множина-степінь? Які використовують при цьому позначення?
13. Чи може множина входити до складу своїх елементів?
14. Які є способи задання множини?
15. Що таке універсум?
ЛАБОРАТОРНА РОБОТА №2. ВІДНОШЕННЯ
Мета: Засвоїти основні поняття та властивості відношень
Теоретичні відомості: Відношення означає будь-який зв’язок між предметами або поняттями. Відношення між парами об’єктів називають бінарними (двомісними).
Приклади бінарних відношень:
• відношення належності;
• включення множин;
• рівність дійсних чисел;
• нерівність (натуральних, дійсних чисел);
• бути братом;
• ділитися на будь-яке натуральне число;
• входить до складу якого-небудь колективу.
Для наведених бінарних відношень можна записати відповідні їм співвідношення:
• ![]()
• ![]()
• ![]()
• ![]()
• ![]()
• ![]() ;
;
• ![]() – староста групи 1КН-09.
– староста групи 1КН-09.
Означення: бінарне відношення А, що діє з множини X у множину Y, називають деяку підмножину X![]() Y (A⊂ X
Y (A⊂ X![]() Y).
Y).
Отже, бінарне відношення встановлює відповідність елементів множини X елементам множини Y. Елемент X називають першою координатою, а елемент Y – другою координатою впорядкованої пари. Множину перших координат називають областю визначення (лівою областю) відношення А. Множину других координат – областю значень (правою областю) відношення А. У таких випадках вважають, що А є відношенням від X до Y. Його називають також відповідністю й позначають X→Y. Відношення може бути подане за допомогою: фактор-множини (множину всіх перерізів відношення А називають фактор-множиною множини Y за відношенням А і позначають Y/A. Вона повністю визначає відношення А), матриці або графа.
Матричний спосіб ґрунтується на поданні відношення A⊂ X![]() Y відповідною йому прямокутною таблицею (матрицею), що складається з нулів та одиниць, де стовпці – перші координати, а рядки – другі, причому на перетині i-го стовпця і j-го рядка буде 1, якщо виконується співвідношення
Y відповідною йому прямокутною таблицею (матрицею), що складається з нулів та одиниць, де стовпці – перші координати, а рядки – другі, причому на перетині i-го стовпця і j-го рядка буде 1, якщо виконується співвідношення ![]() , або 0 – якщо воно не виконується, рис.2.1.
, або 0 – якщо воно не виконується, рис.2.1.
|
|
|
|
|
|
|
|
1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 0 |
Матриця повного відношення – це квадратна матриця, яка складається лише з 1; матриця тотожного (діагонального) відношення – це квадратна матриця, яка складається з 0 та 1 по головній діагоналі; матриця порожнього відношення – це квадратна матриця. Що складається лише з 0.
Відношення також можна зобразити за допомогою орієнтованого графа. Його вершини відповідають елементам множини X та Y, а дуга спрямована від вершини![]() до
до ![]() , означає, що співвідношення
, означає, що співвідношення ![]() виконується, рис.2.2.
виконується, рис.2.2.
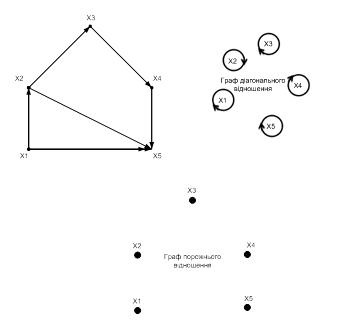
Оскільки відношення – це множини над ними можуть виконуватися всі теоретико-множинні операції. Крім того, виділяють специфічні для відношень операції: обернення (симетризація) і композиція.
Відношення симетричне (обернене) деякому відношенню A⊂ X![]() Y, позначають як
Y, позначають як ![]() , воно є підмножиною множини Y
, воно є підмножиною множини Y![]() X, утвореною тими парами
X, утвореною тими парами ![]() , для яких
, для яких ![]() .
.
Композиція відношень - нехай дано три множини X, Y, Z і два відношення A⊂ X![]() Y, та В⊂ Y
Y, та В⊂ Y![]() Z. Композиція відношень А та В є відношенням С, що складається з усіх тих пар
Z. Композиція відношень А та В є відношенням С, що складається з усіх тих пар ![]() , для яких існує таке
, для яких існує таке ![]() , що
, що ![]() й
й ![]() . Позначаємо композицію відношень символом
. Позначаємо композицію відношень символом ![]() . Тоді:
. Тоді:
![]() .
.
Властивості відношень
Нехай А бінарне відношення у множині X (![]() ). Тоді відношення А є:
). Тоді відношення А є:
• рефлексивним, якщо![]() , тобто воно завжди виконується між елементом іним самим (
, тобто воно завжди виконується між елементом іним самим (![]() ). Як приклад такого відношення можна навести відношення нестрогої нерівності (
). Як приклад такого відношення можна навести відношення нестрогої нерівності (![]() ) на N, Z та R;
) на N, Z та R;
• антирефлексивним, якщо ![]() . Тобто якщо співвідношення
. Тобто якщо співвідношення ![]() виконується, то
виконується, то ![]() . Це приклад відношення строгої нерівності на N, Z та R, відношення «бути старшим» у множині людей;
. Це приклад відношення строгої нерівності на N, Z та R, відношення «бути старшим» у множині людей;
• симетричним якщо ![]() , тобто у разі виконання співвідношення
, тобто у разі виконання співвідношення ![]() виконується співвідношення
виконується співвідношення ![]() . Як приклад відношення можна навести відстань між двома точками на площині, відношення «бути братом» у множині чоловіків;
. Як приклад відношення можна навести відстань між двома точками на площині, відношення «бути братом» у множині чоловіків;
• асиметричним, якщо ![]() , тобто з двох співвідношень
, тобто з двох співвідношень ![]() і
і ![]() щонайменше одне не виконується. Як приклад такого відношення можна навести відношення «бути батьком» у множині людей, відношення строгого включення в множину всіх підмножин деякого універсуму. Очевидно, якщо відношення асиметричне, то воно й анти рефлексивне;
щонайменше одне не виконується. Як приклад такого відношення можна навести відношення «бути батьком» у множині людей, відношення строгого включення в множину всіх підмножин деякого універсуму. Очевидно, якщо відношення асиметричне, то воно й анти рефлексивне;
• антисиметричним, якщо![]() , тобто обидва співвідношення
, тобто обидва співвідношення ![]() та
та ![]() одночасно виконуються тоді й тільки тоді, коли
одночасно виконуються тоді й тільки тоді, коли ![]() . Як приклад можна навести нестрогу нерівність (
. Як приклад можна навести нестрогу нерівність (![]() ) на N, Z та R;
) на N, Z та R;
• транзитивним, якщо![]() , тобто з виконанням співвідношень
, тобто з виконанням співвідношень ![]() й
й ![]() виливає співвідношення
виливає співвідношення ![]() . Як приклад можна навести відношення «бути дільником» у Z, «бути старшим» у множині людей [1].
. Як приклад можна навести відношення «бути дільником» у Z, «бути старшим» у множині людей [1].
Завдання до лабораторної роботи
1. Розробити алгоритм та програму побудови матриці і графу заданого відношення (варіант за списком групи).
2. Скласти алгоритм і розробити програму, котра у заданому векторі А(27) міняє місцями перший елемент з останнім, другий з передостаннім і т.д.
3. Скласти програму транспонування заданої квадратної матриці А(10,10) без використання додаткової матриці.
4. Кажуть, що матриця А(n, n) має «сідлову» точку, якщо деякий елемент матриці є найменшим по величині в стрічці і найбільшим в стовбці, тобто ![]() є «сідловою» точкою, якщо
є «сідловою» точкою, якщо ![]() , де 1 ≤ k ≤ n. Написати програму для знаходження і друку індексів елемента матриці, що є «сідловою» точкою. Якщо матриця не має «сідлової» точки, о надрукувати відповідне повідомлення.
, де 1 ≤ k ≤ n. Написати програму для знаходження і друку індексів елемента матриці, що є «сідловою» точкою. Якщо матриця не має «сідлової» точки, о надрукувати відповідне повідомлення.
5. Написати програму формування масиву А(100), елементами якого є перші 100 чисел (в зростаючому порядку) множини М, що визначається наступним чином:
а) число 1 належить М;
б) якщо число X належить М, то Y=2*X+1 і Z=3*X+1 також належить М, причому однакових чисел М немає;
в) ніякі інші числа не належть М.
Контрольні питання
1. Що таке бінарне відношення? Наведіть приклади.
2. Що таке повне, тотожне і порожнє відношення?
3. Що таке функціональне відношення?
4. Що таке сюр’єкція, ін’єкція, бієкція?
5. Що таке відношення еквівалентності?
6. Які приклади ілюструють відношення нестрогого порядку?
7. Які приклади ілюструють відношення строгого порядку?
8. Які способи подання відношення ви знаєте?
ЛАБОРАТОРНА РОБОТА №3. АЛГОРИТМИ
Мета: Ознайомитись з поняттям алгоритму та його властивостями.
Теоретичні відомості: З давніх часів у математиці склалося інтуїтивне уявлення про алгоритми як формальне розпорядження, що визначає сукупність операцій і порядок їх виконання для розв’язання задач певного типу. Термін походить від латинської вимови (Algorithmi) імені середньовічного узбецького математика аль-Харезмі, який ще в IX ст. сформулював правила, що дають змогу складати та розв’язувати квадратні рівняння [1].
Отже, до уточнення поняття «алгоритм» у математиці були поширені дві точки зору:
1. Усі проблеми є алгоритмічно розв’язуваними. Проте алгоритми для вирішення деяких з них не знайдено, оскільки не вистачає засобів у сучасній математиці для його побудови. Прихильники цієї думки вважали, що для вирішення проблем, які називають алгоритмічно нерозв’язуваними, просто не вистачає засобів сучасної математики, побудова шуканих алгоритмів – справа майбутнього.
2. Існують класи задач, для розв’язання яких узагалі не існує алгоритмів. Тобто, деякі проблеми не можна вирішувати механічно за допомогою формальних міркувань та обчислень. Ці проблеми потребують творчого мислення. Це дуже сильне твердження, адже воно поширюється на всі майбутні часи та засоби.
Починаючи з 1935 року було запропоновано кілька уточнень поняття «алгоритму». Математики погодились із тим, що уточнені поняття адекватно виражають інтуїтивне уявлення про алгоритми. Для цього є такі підстави:
• доведено, що всі відомі на цей час уточнені поняття алгоритму еквівалентні між собою;
• усі алгоритми в точному розумінні є алгоритмами в інтуїтивному розумінні;
• усі відомі алгоритми в інтуїтивному розумінні можна «промоделювати» алгоритмами в точному розумінні.
Традиційно процес розв’язування задачі на ЕОМ складається з таких етапів:
• постановка задачі, тобто чітке її формулювання із зазначенням мети, яку потрібно досягти. Тут виділяються початкові дані, результати і визначається зв’язок між початковими даними та результатами;
• створення математичної моделі, тобто визначення математичних співвідношень (формули, рівнянь, тощо), що пов’язують результати з початковими даними;
• розроблення алгоритму розв’язання задачі, тобто побудова схеми (набору інструкцій) цього процесу;
• написання програми, тобто запис алгоритму розв’язання задачі мовою, зрозумілою для ЕОМ;
• налагодження програми, тобто пошук помилок й усунення їх;
• розв’язання задачі на комп’ютері, тобто розрахунки за готовою програмою та аналіз отриманих результатів.
Отже, можна сформулювати основні вимоги до алгоритмів:
• будь-який алгоритм застосовується для початкових даних і видає результати. У технічних термінах це означає, що алгоритм має входи й виходи. Крім того, під час роботи алгоритму з’являються проміжні результати, що використовуються далі. Отже, кожен алгоритм має справу з початковими, проміжними і вихідними даними;
• дані для їх розміщення потребують пам’яті. Пам’ять вважається однорідною і дискретною, тобто складається з однакових комірок, причому кожна комірка може містити один символ алфавіту даних. Отже, одиниці обсягу даних і пам’яті узгоджено. При цьому пам'ять може бути нескінченною;
• як виконавець алгоритму можуть виступати людина, різні технічні пристрої, наприклад робот або ЕОМ. У будь-якому разі має бути досягнута визначена мета, інакше вся виконувана послідовність втрачає зміст.
Проте навіть під час виконання цих вимог не будь-яка послідовність дій є алгоритмом. Для цього потрібно виконати кілька умов, що визначають властивості алгоритму:
1) детермінованість – визначення кроків алгоритму, тобто після кожного кроку або зазначається, який крок слід робити далі, або дається команда на зупинку, після чого робота алгоритму вважається закінченою. Ця властивість означає, що застосування алгоритму до тих самих даних має привести до одного і того самого результату;
2) масовість – алгоритм може бути використаний для розв’язання цілого класу задач одного типу, наприклад квадратного рівняння з різними коефіцієнтами;
3) результативність (скінченість, збіжність) – виконання алгоритму має або закінчуватися результатом, або інформацією про те, чому не може бути отриманий результат, причому множина різних кроків, з яких складено алгоритм, є скінченною;
4) зрозумілість – алгоритм має бути зрозумілим будь-якому виконавцю, який має виконувати кожну команду алгоритму у строгій відповідності з її призначенням;
5) дискретність – можливість розбиття алгоритму на скінченну кількість етапів, причому результати попереднього етапу є вхідними для наступного.
Отже, кожен алгоритм будується з розрахунку на конкретного виконавця і відповідним чином подається.
Потрібно розрізняти: опис алгоритму (інструкцію або програму); механізм його реалізації (наприклад, ЕОМ), що включає засоби пуску, зупинення, реалізації елементарних кроків, видачі результатів та забезпечення детермінованості, тобто керування ходом обчислення; процес реалізації алгоритму, тобто послідовність кроків, яка буде породжена у разі застосування алгоритму до конкретних даних. Опис алгоритму і механізм його реалізації скінченні [1].
Приклад 1. Розглянемо як приклад алгоритму таку класичну задачу: дано два натуральні числа X та Y; потрібно знайти їх найбільший спільний для ник (GCD). У теорію алгоритмів розв’язання цієї задачі ввійшло під назвою алгоритму Евкліда. Метод її розв’язання є таким:
Крок 1. Початок.
Крок 2. Ввести для розгляду числа X та Y.
Крок 3. Якщо X=Y, то перейти до кроку 7, інакше - до кроку 4.
Крок 4. Якщо X<Y, то перейти до кроку 5, інакше – до кроку 6.
Крок 5. Зменшити Y на значення X, перейти до кроку 3.
Крок 6. Зменшити X на значення Y, перейти до кроку 3.
Крок 7. Прийняти GCD таким, що дорівнює X.
Крок 8. Кінець.
Це був приклад числового алгоритму, який зводить розв’язання наведеної задачі до арифметичних дій над числами. Існує інший тип алгоритмів, що містять розпорядження, яке стосується не цифр, а об’єктів будь-якої природи. Це логічні алгоритми.
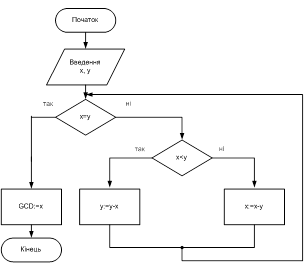
Є три основних типи процесів оброблення інформації: лінійний, розгалужувальний та циклічний. За лінійного процесу оброблення інформації здійснють послідовно, одна дія за іншою, і кожний етап алгоритму виконують лише один раз. За розгалужувального процесу інформацію обробляють одним з двох можливих способів, тобто ті чи інші дії виконують залежно від певної умови. За циклічного процесу ті самі дії з оброблення інформації потрібно виконати багаторазово. Їм відповідають базові структури (конструкції) алгоритмів: проходження (лінійна структура), розгалуження (структура, що розгалужується), повторення (циклічна структура).
Такий граф, в якому вершинам відповідають кроки, а ребрам – переходи між ними, називають схемою алгоритму. Його вершини можуть бути двох типів: вершини, з яких виходить одне ребро (їх називають операторами) і вершини, з яких виходять два ребра (їх називають логічними умовами або предикатами). Крім того, існує єдиний оператор кінця, з якого не виходить жодне ребро, та єдиний оператор початку.
Приклад 2. Типовим прикладом логічних алгоритмів може бути алгоритм пошуку шляху в скінченному лабіринті. Задачу цю розв’язано ще до нашої ери за допомогою відомої нам Аріадни. Лабіринт зручно зображати у вигляді графа, де вершини – це майданчики лабіринту, дуги – його коридори. Нехай потрібно з’ясувати, чи досяжний майданчик f із майданчика a, і якщо це так, то знайти шлях з а в f, а якщо ні – повернутися в а.
Припускається, що заздалегідь нічого невідомо про будову цього лабіринту.
Нехай людина, яка шукає шлях у лабіринті, має у своєму розпорядженні нитку, кінець якої закріплено на майданчику а, та, рухаючись по лабіринту, може розмотувати клубок (P) або, навпаки, намотувати (Н) на нього нитку. Можна робити позначки на прохідних коридорах і розрізняти потім коридори ще жодного разу не пройдені (зелені - З), пройдені один раз (жовті - Ж) та пройдені двічі (червоні - Ч).
Метод пошуку може бути заданий такою схемою:
1) майданчик f – зупинка (мету досягнуто);
2) петля (П) – намотування нитки (від майданчика розходяться принаймні два жовті коридори);
3) зелена вулиця (ЗВ) – розмотування нитки (від майданчика виходить принаймні один зелений коридор);
4) майданчик а – зупинка (початковий пункт);
5) відсутність усіх попередніх ознак (ВО) – намотування нитки.
Потрапивши на який-небудь майданчик, потрібно звірити зі схемою ознак у зазначеному порядку і зробити черговий хід відповідно до першої виявленої ознаки, не перевіряючи ірнших ознак доти, доки не настане зупинка [1].
Завдання до лабораторної роботи
Задача про Ханойські башти. Є три стержні з номерами 1, 2, 3. На 1 стержень надіто N дисків різного діаметру так, що вони створюють піраміду. Розробити програму для друку послідовностей переміщень дисків з стержня на стержень, необхідних для переносу піраміди з 1 стержня на 3 стержень з використанням стержня 2 в якості допоміжного. При цьому за одне переміщення потрібно переносити тільки один диск. Диск більшого діаметру не повинен поміщатися на диск меншого діаметру. Доведено, для N-дисків мінімальна кількість необхідних переміщень дорівнює ![]() .
.
Контрольні питання
1. Які основні вимоги до алгоритмів?
2. Що таке примітивна рекурсія?
3. Які основні властивості алгоритмів?
4. Як формально описується машина Тюринга (МТ)?
5. Що таке внутрішній і зовнішній алфавіти машини Тюринга (МТ)?
6. Що таке конфігурування на стрічці МТ?
7. Які операції виконуються над МТ?
8. Що таке алгоритм?
9. Які етапи розв’язання задачі на ЕОМ ви знаєте?
ЛАБОРАТОРНА РОБОТА №4. МІНІМІЗАЦІЯ ЛОГІЧНИХ ФУНКЦІЙ МЕТОДОМ ДІАГРАМ ВЕЙЧА
Мета: Ознайомитись з мінімізацією логічних (мулевих) функцій методом Вейча
Теоретичні відомості: Популярність двійкової системи числення багато в чому визначається простотою виконання арифметичних дій. Існують такі формальні правила двійкової арифметики:
1. Додавання – диз’юнкція, АБО, ![]() .
.
0+0=0;
0+1=1;
1+0=1;
1+1=(1)0 (перенос в старший розряд (1))
![]()
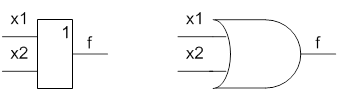
2. Множення – кон’юкція, ![]()
0*0=0;
0*1=0;
1*0=0;
1*1=1.
![]()
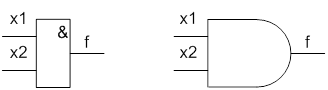
3. Заперечення – функція НІ
![]()

4. Віднімання
0-0=0;
1-0=1;
1-1=0;
0-1=(1)1 (позичка в старшому розряді)
Кон’юнкція, диз’юнкція, заперечення (функції І, АБО, НЕ) використовують основні положення алгебри логіки, нескладно впевнитися в істинності восьми аксіом [2].
Якщо ![]() – деяка логічна змінна, тоді:
– деяка логічна змінна, тоді:
a. ![]() ;
;
b. ![]()
c. ![]()
d. ![]()
e. ![]()
f. ![]()
g. ![]()
h. ![]()
Диз’юнкція і кон’юнкція мають властивості, які аналогічні властивостям звичайних операцій додавання і множення:
1. Властивість асоціативності (сполучний закон) [2]:
![]() ;
;
![]() ;
;
2. Властивість комутативності (переставний закон) [2]:
![]() ;
;
![]() ;
;
3. Властивість дистрибутивності (розподільний закон) [2]:
• кон’юнкції відносно диз’юнкції
![]() ;
;
• диз’юнкції відносно кон’юнкції
![]() ;
;
Властивості дійсні при зміні знака + на ![]() , знака * на
, знака * на ![]() .
.
Властивість дистрибутивності фактично визначає правила розкриття дужок або взяття в дужки логічних виразів.
Закон де Моргана:
![]()
![]()
Очевидно, що:
![]()
![]()
Аксіоми алгебри логіки:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Визначення: мінімальною формою представлення перемикальної функції називають таку форму, яка не допускає більше ніяких спрощень. Процес спрощення перемикальної функції з метою отримання мінімальної форми називають мінімізацією [2].
Для мінімізації функції використовують різні методи послідовного виключення змінних:
1. За допомогою законів і тотожностей алгебри логіки;
2. Методом мінімізуючих карт Карно (діаграм Вейча).
Карта Карно для ДНФ (діаграма Вейча для КНФ) є аналогом таблиці істинності, зображеній у спеціальній формі. Значення змінних розташовані у заголовках рядків і стовпців карти. Кожній конституенті одиниці функції відповідає одна комірка (клітинка) таблиці. Нуль або одиниця в комірці визначає значення функції на даній інтерпретації. Значення змінних розташовані так, щоб сусідні (що мають спільну межу) рядки і стовпці відрізнялися значенням тільки однієї змінної.
Розглянемо приклад мінімізації логічної функції ![]() , котра задана набором:
, котра задана набором:
| х1 | х2 | х3 | х4 | |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 |
| 14 | 1 | 1 | 1 | 0 |
| 15 | 1 | 1 | 1 | 1 |
| х1 | х2 | х3 | х4 | |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
Нехай наша функція задана таблицею 2.
На рисунку покажемо приклад умовного розміщення 4 змінних на мінімізуючій карті:
|
|
|
|
|
||
|
|
1100 12 |
1110 14 |
0110 6 |
0100 4 |
|
|
1101 13 |
1111 15 |
0111 7 |
0101 5 |
|
|
|
|
1001 9 |
1011 11 |
0011 3 |
0001 1 |
|
|
1000 8 |
1010 10 |
0010 2 |
0000 0 |
|
|
|
|
|
|
|
|
|
Для нашого випадку діаграма Вейча буде мати наступний вигляд:
|
|
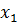
|
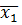
|
|
|
|||
|
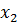 |
1 |
|
|
1 | 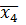 |
|
| 1 |
|
1 | 1 |  |
x10x -> x2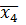 |
||
| 1 | 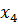 |
||||||
10х1 ->х1 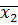 х4 х4 |
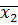
|
1 | 1 | 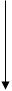 |
|||
|
|
|
|
||||
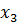 |
|
|
|||||
|
|
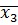 |
|
0x11->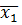 x3x4 x3x4 |
|||
![]() =V(3,4,5,7,9,11,12,13) або
=V(3,4,5,7,9,11,12,13) або
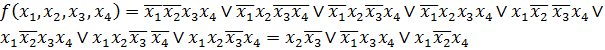 .
.
Аналогічну відповідь можна отримати використовуючи закони логіки Буля для спрощення цього виразу [2].
Завдання до лабораторної роботи
1) Знайти мінімальні функції методом діаграм Карно, Вейча. Функції задані номерами конституент одиниці таким чином:
![]()
![]()
![]()
![]()
![]()
![]()
Побудувати за отриманим результатом відповідну йому логічну схему.
2) Побудувати карти Карно для таких функцій:
• f(x, y, z, t) = xyzt ˅ ![]() yzt ˅
yzt ˅ ![]() ˅ xy
˅ xy ![]() ;
;
• f(x, y, z, t) = x![]() zt ˅
zt ˅ ![]() y
y![]() t ˅
t ˅ ![]() ˅
˅ ![]() y
y ![]() ;
;
• f(x, y, z, t) = ![]() yz
yz![]() ˅ x
˅ x![]() t ˅
t ˅ ![]() ˅ xyz
˅ xyz![]() ;
;
• f(x, y, z, t) = xy![]() t ˅
t ˅ ![]() yz
yz![]() ˅
˅ ![]() ˅
˅ ![]() y
y![]() t;
t;
• f(x, y, z, t) = ![]() yzt ˅
yzt ˅ ![]() ˅ xyzt ˅
˅ xyzt ˅ ![]() ;
;
• f(x, y, z, t) = ![]() ˅
˅ ![]() t ˅
t ˅ ![]() ˅ xyzt.
˅ xyzt.
Контрольні питання
1. Що таке булеві або логічні змінні?
2. Як будують таблицю істинності булевої функції?
3. Перелічіть булеві функції однієї змінної.
4. Скільки існує булевих функцій від n змінних?
5. Наведіть приклади рівносильних функцій.
6. Як формують основні тотожності алгебри Буля?
7. Як довести комутативні закони булевої алгебри?
8. Як довести асоціативні закони булевої алгебри?
9. Як довести дистрибутивні закони булевої алгебри?
10. Дайте визначення алгебри логіки.
11. Як утворюють мінімальні форми за допомогою діаграм Карно-Вейча?
12. Які особливості задачі мінімізації функцій в геометричній формі?
ЛАБОРАТОРНА РОБОТА №5. ОСНОВНІ ПОНЯТТЯ ТЕОРІЇ ГРАФІВ
Мета: Ознайомитись з графами та алгоритмами, які можна виконувати над ними
Теоретичні відомості: Нехай V – довільна множина, E – деяка сукупність пар вигляду ![]() ), де
), де ![]() . Термін «сукупність» означає можливість наявності кількох однакових пар вигляду
. Термін «сукупність» означає можливість наявності кількох однакових пар вигляду ![]() ) і пар
) і пар ![]() ).
).
Упорядковану пару ![]() , що складається з множини V та сукупності E, називається графом із множиною вершин V і множиною ребер E. При цьому елементи множини V зображають точками на площині, а ребра
, що складається з множини V та сукупності E, називається графом із множиною вершин V і множиною ребер E. При цьому елементи множини V зображають точками на площині, а ребра ![]() ) відрізками (прямолінійними або криволінійними), які з'єднують точки
) відрізками (прямолінійними або криволінійними), які з'єднують точки ![]() та
та ![]() [1].
[1].
Граф називається скінченним, якщо множина його вершин і ребер є скінченними. Множину вершин графа G позначають V(G), а множину ребер – E(G). Кількість вершин графа ![]() , а кількість ребер
, а кількість ребер ![]() .
.
Графи зручно зображувати графічно, що і зумовило появу їх назви.
Кількість вершин графа ![]() називають його порядком.
називають його порядком.
Кількість ребер графа, інцидентних деякій вершині ![]() , називають локальним степенем, або просто степенем, вершини
, називають локальним степенем, або просто степенем, вершини ![]() і позначають
і позначають ![]() .Якщо
.Якщо ![]() , то вважають, що:
, то вважають, що:
1. Вершини ![]() та
та ![]() суміжні;
суміжні;
2. Вершини ![]() та
та ![]() є кінцями ребра e;
є кінцями ребра e;
3. Вершини ![]() та
та ![]() – інцидентні ребру е;
– інцидентні ребру е;
4. Ребро е – інцидентне вершинам ![]() та
та ![]() .
.
Два ребра називаються суміжними, якщо обидва вони є інцидентними одній вершині.
Множина ребер Е може бути порожньою (рис. 5.1). Такий граф називають нуль-графом і позначають ![]() . Якщо множина вершин V – порожня. То порожньою є також множина Е. Такий граф називають порожнім. Лінії, що зображають ребра графа, можуть перетинатися, але точки перетину не є вершинами; різні ребра можуть бути інцидентами тій самій парі вершин, такі ребра називаються кратними. Цей випадок відповідає наявності кількох однакових пар
. Якщо множина вершин V – порожня. То порожньою є також множина Е. Такий граф називають порожнім. Лінії, що зображають ребра графа, можуть перетинатися, але точки перетину не є вершинами; різні ребра можуть бути інцидентами тій самій парі вершин, такі ребра називаються кратними. Цей випадок відповідає наявності кількох однакових пар ![]() . Граф, що містить кратні ребра називають мультиграфом. Ребро може з’єднувати деяку вершину саму з собою, таке ребро називають петлею. Цей випадок відповідає наявності в множині Е пар вигляду
. Граф, що містить кратні ребра називають мультиграфом. Ребро може з’єднувати деяку вершину саму з собою, таке ребро називають петлею. Цей випадок відповідає наявності в множині Е пар вигляду ![]() . Граф із петлями та кратними ребрами називають псевдографом.
. Граф із петлями та кратними ребрами називають псевдографом.
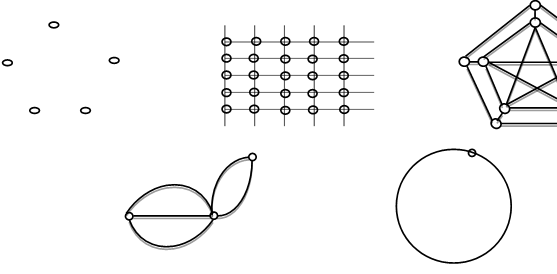
Фрагмент нескінченного графа зображено на рисунку. Його вершини – це точки площини з цілими координатами ![]() , а ребра, що з’єднують їх, - горизонтальні і вертикальні відрізки. Графи, які найчастіше розглядають, є скінченними, тобто скінченні множини їх елементів (вершин і ребер). Їх і розглядатимемо. Скінченний неорієнтований граф без петель і кратних ребер називають звичайним. Якщо пари
, а ребра, що з’єднують їх, - горизонтальні і вертикальні відрізки. Графи, які найчастіше розглядають, є скінченними, тобто скінченні множини їх елементів (вершин і ребер). Їх і розглядатимемо. Скінченний неорієнтований граф без петель і кратних ребер називають звичайним. Якщо пари ![]() вважають впорядкованими, то граф є орієнтованим. Інакше граф називають неорієнтованим. Ребра орієнтованого графа прийнято називати дугами та зображати напрямленими відрізками, як на рисунку 5.2.
вважають впорядкованими, то граф є орієнтованим. Інакше граф називають неорієнтованим. Ребра орієнтованого графа прийнято називати дугами та зображати напрямленими відрізками, як на рисунку 5.2.
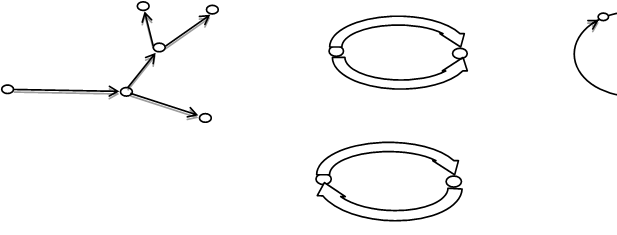
У разі зображення орієнтованих графів напрямки дуг позначають стрілками. Орієнтований граф може мати кратні дуги, петлі, а також дуги, що з’єднують одні і ті ж самі вершини, але у зворотних напрямках. Кожному неорієнтованому графу можна поставити у відповідність орієнтований граф з тією самою множиною вершин, в якій кожне ребро замінено двома орієнтованими ребрами, що є інцидентними тим самим вершинам і мають зворотні напрямки. Таку відповідність називатимемо канонічною. Граф, що має як ребра, так і дуги називають мішаним.
Про дугу ![]() кажуть, що вона виходить із вершини
кажуть, що вона виходить із вершини ![]() та входить у вершину
та входить у вершину ![]() . Іноді вершини
. Іноді вершини ![]() та
та ![]() називають відповідно початком та кінцем дуги
називають відповідно початком та кінцем дуги ![]() . Домовимося позначати орграфи літерою
. Домовимося позначати орграфи літерою ![]() або
або ![]() з індексом (
з індексом (![]() ).
).
Завдання до лабораторної роботи
Вивчити алгоритм Беллмана (він дає змогу за таблицею величин ![]() визначити мінімальний шлях у зваженому орієнтованому графі) [1].
визначити мінімальний шлях у зваженому орієнтованому графі) [1].
1. Знайти мінімальний шлях з ![]() у
у ![]() в орієнтованих графах, заданих матрицею суміжності:
в орієнтованих графах, заданих матрицею суміжності:
а) 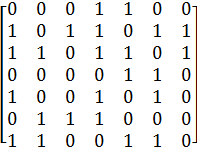
б) 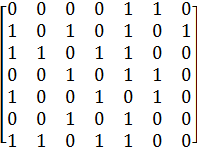
в) 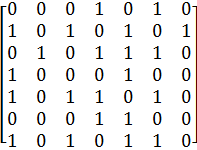
2. Виконати розв’язок запропонованої задачі, якщо необхідно визначити мінімальний шлях з ![]() у
у ![]() у зважених орієнтованих графах із заданими матрицями ваг:
у зважених орієнтованих графах із заданими матрицями ваг:
а)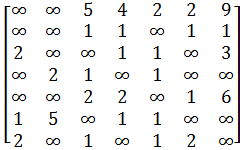
б)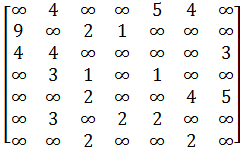
в)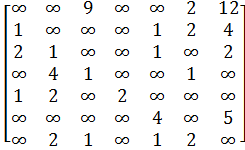
Контрольні питання
1. Що таке граф, ребро, дуга, порядок графа?
2. Дайте визначення нуль-графа.
3. Дайте визначення порожнього графа.
4. Що таке кратні ребра?
5. Дайте визначення петлі.
6. Як задати граф за допомогою матриці суміжності?
ЛАБОРАТОРНА РОБОТА №6 МАТРИЧНІ СПОСОБИ ПРЕДСТАВЛЕННЯ ГРАФІВ
Мета: Вивчення матричних способів представлення графів.
Теоретичні відомості: Останнім часом теорія графів стала простим, доступним і потужним засобом вирішення питань, що відносяться до широкого кола проблем. Це проблеми проектування інтегральних схем і схем управління, дослідження автоматів, логічних ланцюгів, блок-схем програм, економіки та статистики, хімії та біології, теорії розкладів і дискретної оптимізації.
Граф G задається множиною точок або вершин x1,x2,...,xn (які позначаються X) і множиною ліній або ребер a1,a2,…,an які позначаються А), що з'єднують між собою всі або частину цих точок. Таким чином, граф G повністю задається (і позначається) парою (X, А).
Якщо ребра орієнтовані, що зазвичай показується стрілкою, то вони називаються дугами, і граф з такими ребрами називається орієнтованим графом (рисунок 6.1 (а)). Якщо ребра не мають орієнтації, то граф називається неорієнтованим (рисунок 6.1 (б)). У разі коли G = (X, А) є орієнтованим графом і ми хочемо знехтувати спрямованістю дуг з множини А, то неорієнтований граф, відповідний G, будемо позначати як G = (X, А).
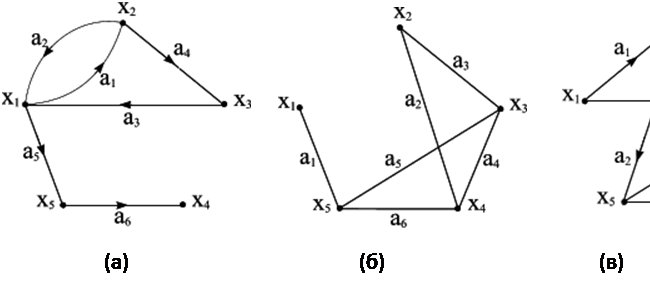
Якщо дуга позначається впорядкованою парою, що складається з початкової та кінцевої вершин (тобто двома кінцевими вершинами дуги), її напрямок передбачається заданим від першої вершини до другої. Так, наприклад, на рисунку 6.1 (а) позначення (x1,x2) відноситься до дуги a1, а (x2,x1) – до дуги a2.
Частіше опис орієнтованого графа G полягає в заданні множини вершин Х та відповідності Г, яка показує, як між собою пов'язані вершини. Відповідність Г називається відображенням множини Х в Х, а граф в цьому випадку позначається парою G = (X, Г).
Для графа на рисунку 6.1 (а) маємо Г(x1)={x2,x5}, тобто вершини x2 і x5 є кінцевими вершинами дуг, у яких початковою вершиною є x1. Г(x2)={x1,x3}, Г(x3)={x1}, Г(x4)= ∅ - порожня множина, Г(x5)={x4}.
У випадку неорієнтованого графа або графа, що містить і дуги, і неорієнтовані ребра (див., наприклад, графи, зображені на рисунках 6. 1 (б) і 6.1 (в)), передбачається, що відповідність Г задає такий еквівалентний орієнтований граф, який виходить з вихідного графа заміною кожного неорієнтованого ребра двома протилежно спрямованими дугами, що з'єднують ті ж самі вершини. Так, наприклад, для графа, наведеного на рисунку 6.1 (б), маємо Г(x5)={x1,x3,x4}, Г(x1)={x5} та інші.
Оскільки, пряма відповідність або образ вершини Г(xi) являє собою множину таких вершин xj∈X, для яких у графі G існує дуга (xi,xj), то через Г-1(xi) природно позначити множину вершин xk, для яких у G існує дуга (xk,xi). Таке відношення прийнято називати зворотною відповідністю або прообразом вершини. Для графа, зображеного на рисунку 6. 1 (а), маємо Г-1(x1)={x2,x3}, Г-1(x2)={x1} і т. д.
Цілком очевидно, що для неорієнтованого графа Г-1(xi)=Г(xi) для всіх xi∈X.
Коли відображення Г діє не на одну вершину, а на множину вершин Xq={x1,x2,...,xq}, то під Г(Xq) розуміють об'єднання Г(x1) ∪Г(x2) ∪... ∪Г(xq), тобто Г(Xq) є множиною таких вершин xj∈X, що для кожної з них існує дуга (xi,xj) у G, де xi∈Xq. Для графа, наведеного на рисунку 6.1 (а), Г({x2,x5})={x1,x3,x4} і Г({x1,x3})={x2,x5,x1}.
Відображення Г(Г(xi)) записується як Г2(xi). Аналогічно "потрійне" відображення Г(Г(Г(xi))) записується як Г3(xi) і т. д. Для графа, зображеного на рисунку 6.1 (а), маємо:
Г2(x1)=Г(Г(x1))=Г({x2,x5})={x1,x3,x4};
Г3(x1)=Г(Г2(x1))=Г({x1,x3,x4})={x2,x5,x1} і т. д.
Аналогічно сприймаються позначення Г-2(xi), Г-3(xi) і т. д.
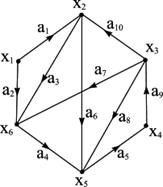
Дуги a=(xi,xj), xi≠xj, що мають спільні кінцеві вершини, називаються суміжними. Дві вершини xi і xjназиваються суміжними, якщо яка-небудь з двох дуг (xi,xj) і (xj,xi) або обидві одночасно присутні в графі. Так, наприклад, на рисунку 6.2 дуги a1, a10, a3 і a6 як і вершини x5 і x3, є суміжними, у той час як дуги a1 і a5 або вершини x1 і x4 не є суміжними.
Число дуг, які починаються у вершині xi , називаються півстепенем «виходу» вершини xi, і, аналогічно, число дуг, які мають xi за кінцеву вершину, називається півстепенем «виходу» вершини xi.
Таким чином, на рисунку 6.2 півстепенені «виходу» вершини x3, позначена через deg+(x3), дорівнює ½Г(x3) ½=3, і півстепені «заходу» вершини x3, позначена через deg-(x3), дорівнює ½Г-1(x3) ½=1.
Очевидно, що сума півстепені «заходу» всіх вершин графа, а також сума півстепені «виходу» всіх вершин дорівнюють загальному числу дуг графа G, тобто
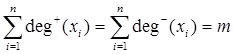
де n - число вершин і m - число дуг графа G;
deg+(xi) – число дуг, що починаються у вершині хі, і аналогічно deg-(xi) число дуг, що закінчуються у вершині хі.
Для неорієнтованого графа G = (X, Г) степінь вершини xi визначається аналогічно - за допомогою співвідношення deg(xi) ≡|Г(xi) |= |Г-1(xi) |.
Петлею називається дуга, початкова та кінцева вершини якої збігаються. На рисунку 6.3, наприклад, дуги a3 і a10 є петлями.
Матриця суміжності
Нехай дано граф G, його матриця суміжності позначається через A=[aij] і визначається наступним чином:
aij=1, якщо в G існує дуга (xi,xj),
aij=0, якщо в G немає дуги (xi,xj).
Таким чином, матриця суміжності графа, зображеного на рисунку 6.3, має вигляд:
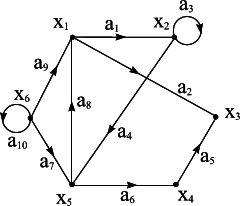
| x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | 0 | 1 | 1 | 0 | 0 | 0 |
| x2 | 0 | 1 | 0 | 0 | 1 | 0 |
| x3 | 0 | 0 | 0 | 0 | 0 | 0 |
| x4 | 0 | 0 | 1 | 0 | 0 | 0 |
| x5 | 1 | 0 | 0 | 1 | 0 | 0 |
| x6 | 1 | 0 | 0 | 0 | 1 | 1 |
Матриця суміжності повністю визначає структуру графа. Наприклад, хі сума всіх елементів рядка хі матриці дає півстепені «виходу» вершини xi, а сума елементів стовпця xi – півстепені «заходу» вершини xi. Множина стовпців, які знаходятся в 1 рядку xi є множина Г(xi), а множина рядків, які мають 1 у стовпці xi збігається з множиною Г-1(xi).
Петлі на графі являють собою елементи, що мають 1 на головній діагоналі матриці, наприклад a22, a66 для графа, зображеного на рисунку 3.
У разі неорієнтованого графа матриця суміжності є симетричною відносно головної діагоналі (рисунок 6.4).
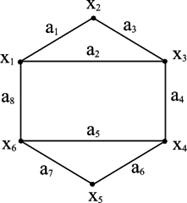
| x1 | x2 | x3 | x4 | x5 | x6 | |
| x1 | 0 | 1 | 1 | 0 | 0 | 1 |
| x2 | 1 | 0 | 1 | 0 | 0 | 0 |
| x3 | 1 | 1 | 0 | 1 | 0 | 0 |
| x4 | 0 | 0 | 1 | 0 | 1 | 1 |
| x5 | 0 | 0 | 0 | 1 | 0 | 1 |
Матриця інцидентності
Нехай дано граф G з n вершинами і m дугами. Матриця інцидентності графа G позначається через B=[bij] і є матрицею розмірності n x m, яка визначається таким чином:
bij=1, якщо xi є початковою вершиною дуги aj;
bij=-1, якщо xi є кінцевою вершиною дуги aj;
bij=0, якщо xi не є кінцевий вершиною дуги aj.
Для графа, наведеного на рисунку 6.3, матриця інцидентності має вигляд:
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | ||
| x1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | -1 | 0 | |
| x2 | -1 | 0 | ±1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| B = | x3 | 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| x4 | 0 | 0 | 0 | 0 | -1 | -1 | 0 | 0 | 0 | 0 | |
| x5 | 0 | 0 | 0 | -1 | 1 | 1 | -1 | 1 | 0 | 0 | |
| x6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | ±1 |
Оскільки кожна дуга інцидентна двом різним вершинам (за винятком випадку, коли дуга утворює петлю), то кожен стовпець містить один елемент, що дорівнює 1, і один – що дорівнює -1. Петля в матриці інцидентності не має адекватного математичного подання (в програмній реалізації допускається задання одного елемента bij=1).
Якщо G є неорієнтованим графом, то його матриця інцидентності визначається таким чином:
bij=1, якщо xi є кінцевою вершиною дуги aj;
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | ||
| x1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| x2 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |
| B = | x3 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| x4 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| x5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | |
| x6 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
bij=0, якщо xi не є кінцевою вершиною дуги aj.
Матриця інцидентності, як спосіб задання графів, успішно застосовується при описі мультиграфі (графів, в яких суміжні вершини можуть з'єднуватися кількома паралельними дугами).
Порядок виконання роботи
1. Одержати завдання у викладача у вигляді одного з двох способів матричного представлення графа:
а) матриця суміжності;
б) матриця інцидентності
2. Скласти алгоритм програми, що реалізує переклад із заданого способу матричного представлення графа в інший, враховуючи при цьому вихідний тип графа (неорієнтований, орієнтований, змішаний).
3. Створити програму, що реалізує переклад із заданого способу матричного представлення графа в інший. Передбачити консольне введення початкових даних і виведення результатів роботи програми на екран.
Контрольні питання
1. Перерахуйте основні способи представлення графів.
2. Покажіть на прикладі пряму і зворотну відповідність для заданої вершини.
3. Чому дорівнює сума степенів усіх вершин неорієнтованого графа?
4. У чому відмінності матричного представлення орієнтованих і неорієнтованих графів?
5. У чому особливості подання графа матрицею суміжності?
6. У чому особливості подання графа матрицею інцидентності?
ЛАБОРАТОРНА РОБОТА № 7 ПОШУК НАЙКОРОТШИХ ШЛЯХІВ У ГРАФАХ
Мета: Вивчення алгоритмів пошуку найкоротших шляхів у графах на прикладі метода динамічного програмування.
Теоретичні відомості: Шляхом (або орієнтованим маршрутом) орієнтованого графу називається послідовність дуг, у якій кінцева вершина будь-якої дуги, що відрізняється від останньої, є початковою вершиною наступної. Так на рисунку 7.1 послідовість дуг μ1={a6, a5, a9, a8, a4}, μ2={a1, a6, a5, a9}, μ3={a1, a6, a5, a9, a10, a6, a4 } є шляхами.
Орієнтованим ланцюгом називається такий шлях, в якому кожна дуга використовується не більше одного разу. Наприклад, згадані вище шляхи μ1 і μ2 є орієнтованими ланцюгами, а шлях μ3 таким не являється, оскільки дуга a6 в ньому використовується двічі.
Маршрут є неорієнтованим "двійником" шляху, і це розглядається у тих випадках, коли можна знехтувати напрямком дуг у графі.
Таким чином, маршрут - це послідовність ребер a1, a2,...,aq, в якій кожне ребро ai, за виключенням, першого і останнього ребер, зв`язане з ребрами ai-1 и ai+1 своїми двома кінцевими вершинами.
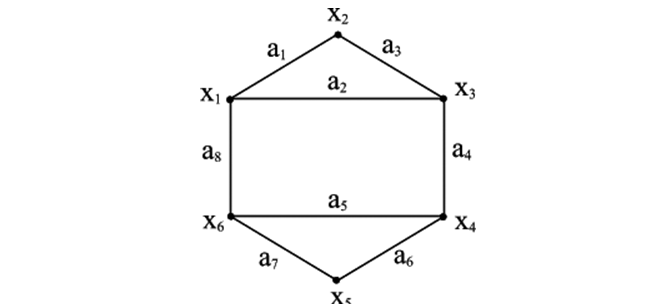
Послідовність дуг на рис. 7.2 μ4={a2, a4, a8, a10}, μ5={a2, a7, a8, a4, a3} и μ6={a10, a7, a4, a8, a7, a2} є маршрутами.
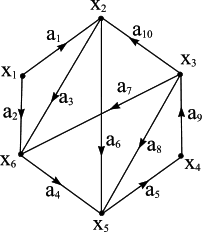
Контуром (простим ланцюгом) називається такий шлях (маршрут), в якому кожна вершина використовується не більше одного разу. Наприклад, шлях μ2 є контуром, а шляхи μ1 і μ3 такими не являються. Очевидно, що контур є також ланцюгом, але обернене твердження є неправильним. Наприклад, шлях μ1 єланцюгом, але не контуром, шлях μ2 є ланцюгом і контуром, а шлях μ3 є ні ланцюгом, ні контуром.
Аналогічно визначається простий ланцюг в неорієнтованих графах. Так, наприклад, маршрут μ4 є простим ланцюгом, маршрут μ5 - ланцюг, а маршрут μ6 не є ланцюгом.
Шлях або маршрут можна зображувати також послідовністю вершин. Наприклад, шлях μ1 можна представити також: μ1={x2, x5, x4, x3, x5, x6} і таке представлення часто виявляється більш корисним в тих випадках, коли виконується пошук контурів або простих ланцюгів.
Іноді дугам графа G відповідають (приписують) числа - дузі (xi,xj) ставиться відповідно деяке число cij, що називається вагою, або довжиною, або вартістю (ціною) дуги. Тоді граф Gназивається зваженим.Іноді вагу (числа vi) приписують вершинам xi графа.
При розгляді шляху μ, представленого послідовністю дуг (a1, a2,...,aq), за його вагу (або довжину, або вартість) беруть число L(µ), рівне сумі ваг всіх дуг, що входять в μ, тобто
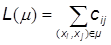
Таким чином, коли слова "довжина", "вартість", "ціна" і "вага" застосовуються до дуг, то вони є еквівалентними за змістом, і в кожному конкретному випадку вибирається таке слово, яке найкраще підходить за змістом .
Довжиною (або потужністю) шляху називається число дуг, що входять в нього.
Задача про найкоротший шлях
Нехай дано граф G=(X,Г), дугам якого приписані ваги, що задаються матрицею С=[сij]. Задача про найкоротший шлях складається з знахождення найкоротшого шляху від даноїпочаткової вершини s до заданої кінцевої вершини (стока) t, за умови, що такий шлях існує:
Знайти µ(s,t) при L(µ)→min, s,t∈Х, t∈R(s),
де R(s) - множина, досяжна з вершини s.
У загальному випадку елементи сij матриці ваг С можуть бути додатніми, від`ємними або нулями. Єдине обмеження в тому, щоб в G не було циклів з сумарною від`ємною вагою. Звідси слідує, що дуги (ребра) графа G не повинні мати від’ємну вагу.
Майже всі методи, що дозволяють розв`язати задачу про найкоротший (s-t)-шлях, дають також (в процесі розв`язання) і всі найкоротші шляхи від s до xi(∀xi∈Х). Таким чином, вони дозволяють розв`язати задачу з невеликими додатковими розрахунковими затратами.
Допускається, що матриця ваг С не задовільняє умову, тобто не обов`язково сij≤сik +сkj для всіх i, j і k. Якщо в графі G дуга (xi, xj) відсутня, то її вага дорівнює ∞.
Ряд задач, наприклад, задачі знахождення в графах шляхів з максимальною надійністю і з максимальною пропускною здатністю, пов`язаних із задачею про найкоротший шлях, хоча в них характеристика шляху (скажімо, вага) є не сумою, а деякою іншою функцією характеристик (ваг) дуг, що створюють шлях. Такі задачі можна переформулювати як задачі про найкоротший шлях і розв`язати їх відповідним чином.
Існує множина методів розв`язання даної задачі, що відрізняються областю застосування і трудомісткістю (Дейкстри, Флойда, динамічного програмування). Серед них найбільшрозповсюдженими є алгоритми, які застосовуютья при розв`язанні задач, і які мають меншу трудомісткість. Ці випадки зустрічаються на практиці доволі часто (наприклад, коли сij є відстанями), тому розгляд цих спеціальних алгоритмів є оправданим.
На практиці задачу про найкоротший шлях часто потрібно розв`язувати для класу орієнтованих ациклічних графів. Такі задачі успішно розв`язувати за допомогою методу динамічногопрограмування.
Метод динамічного програмування
Пряма ітерація. Нехай вершини пронумеровані так, що дуга (xi,xj) завжди орієнтована від вершини xi до вершини xj, що має більший номер. Для ациклічного графа така нумерація завжди можлива і виконується дуже легко. При цьому початкова вершина s має номер 1, а кінцева t - номер n.
Нехай λ(xi) – мітка вершини xi, дорівнює довжині найкоротшого шляху від 1 до xi, s – початкова вершина, t – кінцева вершина.
Крок 1. Покласти λ(s)=0, λ(xi) = ∞ для всіх вершин xi ∈ X/s; i=1;
Крок 2. i=i+1. Присвоїмо вершині xj мітку λ(xj), - рівну довжині найкоротшого шляху від 1 до xj, використовуючи для цього відношення
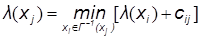
Крок 3. Повторяти п.2. до тих пір, поки остання вершина n не отримає мітку λ(t).
Необхідно зазначити, що якщо вершина xj позначена, то мітки λ(xi) відомі для всіх вершин xi∈Г-1(xj), так як відповідно зі способом нумерації це означає, що xi<xj і, таким чином вершини xi уже позначені в процесі застосування алгоритма.
Мітка λ(t) дорівнює довжині найкоротшого шляху від s до t. Дуги, що утворюють шлях, можуть бути знайдені способом послідовного повернення. А саме дуга (xi,xj), згідно (3), належить шляху тоді і тільки тоді, коли
Обернена ітерація: починаючи з вершини t, що має номер n, припустимо, що на кожному кроці xj дорівнює такій вершині (скажімо, xj*), для якої виконується відношення (4), і так продовжуємо до тих пір, поки не буде досягнуто початкової вершини (тобто поки не буде xj*≡s).
Очевидно, що мітка λ(xj) вершини xj дає довжину найкоротшого шляху μ від s до xj.
Алгоритм топологічного сортування
В деяких випадках початковий граф є ациклічним, але має неправильну нумерацію – містить дуги (xj,xi), орієнтовані від вершини xj до вершини xi, що мають менший номер (j>i). Для успішного знаходження найкоротшого шляху за допомогою методу динамічного програмування до такого графу спочатку застосовується алгоритм топологічного сортування вершин.
Алгоритм топологічного сортування вершин дуже простий. Він дозволяє не тільки правильно перенумерувати вершини графа, але і визначити його ациклічність.
Крок 1. Покласти i=n, де n – число вершин графа G.
Крок 2. В графі визначається вершина xk, для якої виконується умова |Г(xk)|=∅ (тобто., вершина, з якої не виходить жодна дуга). Вершина xk отримує порядковий номер i(перенумеровується) і виключається з подальшого розгляду разом з усіма вхідними в неї інцидентними дугами. i=i–1.
Крок 3. Повторяти п.2. до тих пір, поки не буде виконано одна з умов:
1) i=1 – досягнута початкова вершина. Вершини графа отримали правильну нумерацію.
2) Неможливо визначити вершину, для якої виконувалася б умова |Г(xk)|=∅. В графі є цикл.
В останньому випадку алгоритм динамічного програмування не застосовується. Для пошуку найкоротших шляхів на такому графі необхідно використовувати більш эфективні методи, наприклад, алгоритм Дейкстри [3].
Контрольний приклад
Для графа, зображеного на рис.7. 3, визначимо найкоротший шлях між вершинами x1 і x7, застосовуючи метод динамічного програмування.
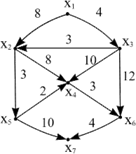
Оскільки граф містить дуги (x3 ,x2) и (x5 ,x4), що мають неправильну нумерацію (від більшого до меншого), необхідно перенумерувати вершини графа, застосовуючи алгоритм топологічного сортування вершин.
В нашому випадку з графа будуть послідовно виключатись вершини x7, x6 , x4, x5, x2, x3, x1. Відповідно, вершини графа отримають нову нумерацію, і граф буде мати вигляд, показанийна рис.7.4 (стара нумерація вершин збережена в дужках).
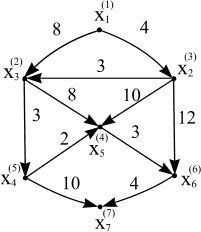
На першому кроці оцінка λ(x1)=0.
Переходимо до вершини x2. Множина Г-1(x2) включає тільки одну вершину x1. Таким чином, оцінка для вершини x2 визначається за формулою (3), буде λ(x2)=min{0+4}=4. Переходимо до вершини x3. Для вершини x3 множина Г-1(x3)={x1, x2}. В цьомувипадку, оцінка буде вибиратись як мінімальна з двох можливих: λ(x3)=min{0+8, 4+3}=7. Для вершини x4 оцінка визначається знову однозначно: λ(x4)=min{7+3}=10. Однак при переході довершини x5 ми отримаємо зразу три вхідних дуги (x2, x5), (x3, x5), (x4, x5).
Застосовуючи формулу (3), визначаємо оцінку для вершини x5:
λ(x5)=min{4+10, 7+8, 10+2}=12.
Далі, аналогічним чином вершина x6 отримає оцінку λ(x6)=min{4+12, 12+3}=15 і, нарешті, вершина x7 отримає оцінку λ(x7)=min{10+10, 15+4}=19.
Таким чином, кінцева вершина x7 шляху µ(x1,x7) досягнута, довжина шляху дорівнює L(µ)=19.
Застосовуючи вираз (4), послідовно визначаємо вершини, які входять в найкоротший шлях. Преміщаючись від кінцевої вершини x7, вибираємо послідовність вершин, для яких вираз(4) приймає значення «істина»: x6, x5, x4, x3, x2, x1, тобто найкоротший шлях проходить послідовно через всі вершини графа.
Дійсно, легко впевнитись в істинності виразів:
λ(x7)= λ(x6)+ c67, (19=15+4);
λ(x6)= λ(x5)+ c56, (15=12+3);
λ(x5)= λ(x4)+ c45, (12=10+2);
λ(x4)= λ(x3)+ c34, (10=7+3);
λ(x3)= λ(x2)+ c23, (7=4+3);
λ(x2)= λ(x1)+ c12, (4=0+4).
Виконуючи перенумерацію вершин графа на вихідну, нарешті визначаємо найкоротший шлях:
µ(x1,x7)={x1, x3, x2, x5, x4, x6, x7}.
Задачу розв`язано.
Результат розв`язання у вигляді виділеного шляху зображено на рис. 7.5. Курсивом «із зірочкою» позначено значення міток вершин λ(xi).
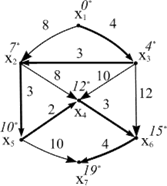
Порядок виконання роботи
1. Отримати завдання у викладача у вигляді вихідного орієнтованого графа.
2. Скласти блок-схему програми, що визначає найкоротший шлях у графі від початкової вершини s до заданої кінцевої вершини t за допомогою метода динамічного програмування.
3. Скласти блок-схему програми, що реалізує алгоритм топологічного сортування з випадковою нумерацією вершин графа.
4. Створити програму, що реалізує метод динамічного програмування і алгоритм топологічного сортування вершин. Вихідний граф задається у вигляді матриці суміжності, якавводиться пострічково за допомогою консолі. Вказівка: для визначення вершин, що входять в множину Г-1(xi) використовуйте j-й стовпчик матриці суміжності.
Контрольні питання
1. Дайте визначення шляху, маршрута, ланцюга, контура.
2. Який граф називається зваженим?
3. Як визначається довжина шляху графа?
4. Задача знаходження найкоротшого шляху в графі.
5. Реалізація методу динамічного програмування для знаходження найкоротшого шляху в графі.
6. Обмеження застосування методу динамічного програмування для знаходження найкоротшого шляху в графі.
7. Що називається правильною нумерацією вершин графа?
8. Застосування алгоритму топологічного сортування для перенумерації вершин графа.
ЛАБОРАТОРНА РОБОТА № 8. ПОБУДОВА НАЙКОРОТШИХ ОСТОВ ДЕРЕВ ГРАФА
Мета : Вивчення методу побудови найкоротшого каркасу дерева графа на прикладі алгоритму Прима-Краскала.
Теоретичні відомості: Одним з найбільш важливих понять теорії графів є дерево.
Неорієнтованим деревом називається зв'язаний граф, який не має циклів.
Суграфом графа G є підграф Gp, що містить всі вершини вихідного графа.
Якщо G = (X, A) - неорієнтований граф з n вершинами, то зв'язний суграф Gp, що не має циклів, називається остовим деревом (остовом або каркасом) графа G.
Для остового дерева справедливе співвідношення:
Легко довести, що остове дерево має такі властивості:
1) остове дерево графа з n вершинами має n-1 ребер (| Xp | = | Ap | -1);
2) існує єдиний шлях, що з'єднує будь-які дві вершини остова графа: ∀xi,xj ∈Xp (i≠j) →∃!μ(xi,xj).
Наприклад, якщо G - граф, показаний на рисунку 8.1 (a), то графи на рисунках 8.1 (б, в) є остовами графа G. З зформульованих вище визначень випливає, що остов графа G можна розглядати як мінімальний пов'язаний остовий підграф графа G.
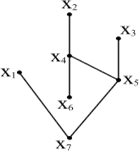
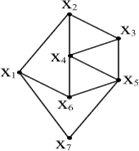
Поняття дерева як математичного об'єкта було вперше запропоновано Кірхгофом у зв'язку з визначенням фундаментальних циклів, застосовуваних при аналізі електричних ланцюгів. Приблизно десятьма роками пізніше Келі знову (незалежно від Кірхгофа) ввів поняття дерева і отримав більшу частину перших результатів в галузі дослідження властивостей дерев. Велику популярність здобула його знаменита теорема:
Теорема Келі. На графі з n вершинами можна побудувати nn-2 остових дерев.
Орієнтоване дерево являє собою орієнтований граф без циклів, в якому півстепені «заходу» кожної вершини, за винятком однієї (вершини r), дорівнює одиниці, а півстепені «заходу» вершини r (названою коренем цього дерева) дорівнює нулю.
На рисунку 8.2 показаний граф, який є орієнтованим деревом з коренем у вершині x1. З наведеного визначення випливає, що орієнтоване дерево з n вершинами має n-1 дуг і зв'язано.
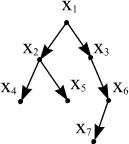
Неорієнтоване дерево можна перетворити в орієнтоване: треба взяти його довільну вершину в якості кореня і ребрам приписати таку орієнтацію, щоб кожна вершина з'єднувалася з коренем (тільки одним) простим ланцюгом.
"Генеалогічне дерево", в якому вершини відповідають особам чоловічої статі, а дуги орієнтовані від батьків до дітей, являє собою добре відомий приклад орієнтованого дерева. Корінь в цьому дереві відповідає "засновнику" роду (особі, яка народилася раніше за інших).
Найкоротший остов графа
У лабораторній роботі досліджується метод прямої побудови найкоротших остовів дерев у зваженому графі (у якому ваги приписані дугами). Найкоротше остове дерево графа застосовується при прокладці доріг (газопроводів, ліній електромереж і т. д.), коли необхідно пов'язати n точок деякої мережі так, щоб загальна довжина "ліній зв'язку" була мінімальною. Якщо точки лежать на евклідовій площині, то їх можна вважати вершинами повного графа G з вагами дуг, рівними відповідним "прямолінійним" відстаням між кінцевими точками дуг. Якщо "розгалуження" доріг допускається тільки в заданих n точках, найкоротше остове дерево графа G буде якраз необхідною мережею доріг, що має найменшу вагу.
Розглянемо зважений зв'язний неорієнтовані граф G = ( X, А ) ; вага ребра ( xi , xj ) позначимо cij . З великого числа остовів графа потрібно знайти один, у якого сума ваг ребр найменша. Така задача виникає, наприклад, в тому випадку, коли вершини є клемами електричної мережі, які повинні бути з'єднані один з одним за допомогою проводів найменшою загальної довжини (для зменшення рівня наведень ). Інший приклад: вершини представляють міста, які потрібно зв'язати мережею трубопроводів; тоді найменша загальна довжина труб, яка повинна бути використана для будівництва (за умови, що за містами "розгалуження" трубопроводів не допускаються), визначається найкоротшим остовом відповідного графа.
Завдання побудови найкоротшого каркасу графа є однією з небагатьох задач теорії графів, які можна вважати повністю вирішеними.
Алгоритм Прима-Краскала
Цей алгоритм породжує остове дерево за допомогою розростання тільки одного піддерева, наприклад Xp, що містить більше однієї вершини . Піддерево поступово розростається за рахунок приєднання ребер ( xi , xj ), де xi ∈ Xp і xj ∉ Xp; причому додане ребро повинне мати найменшу вагу cij . Процес продовжується до тих пір, поки число ребер в Ap не стане рівним n - 1. Тоді піддерево Gp = ( Xp , Ap ) буде потрібним остовим деревом. Вперше така операція була запропонована Примом і Краскалом (з різницею - в способі побудови дерева), тому даний алгоритм отримав назву Прима-Краскала.
Алгоритм починає роботу з включення до піддерева початкової вершини. Оскільки остове дерево включає всі вершини графа G, то вибір початкової вершини не має принципового значення. Будемо кожній черговій вершині привласнювати позначку β (xi) = 1, якщо вершина xi належить піддереву Xp і β (xj) = 0 - в іншому випадку.
Алгоритм має вигляд:
Крок 1. Нехай Xp = {x1}, де x1 - початкова вершина, і Ap = ∅ (Ap є множиною ребер, що входять до остового дерева). Вершині x1 присвоїти позначку β(x1) = 1. Для кожної вершини xi∉ Xp привласнити β (xi) = 0.
Крок 2. З усіх вершин xj ∈ Г (Xp), для яких β (xj) = 0, знайти вершину xj* таку, що
Крок 3. Оновити дані: Xp = Xp ∪ {xj*}; Ap = Ap ∪![]() . Присвоїти β (xj*) = 1.
. Присвоїти β (xj*) = 1.
Крок 4. Якщо | Xp | = n, то зупинитися. Ребра в Ap утворюють найкоротший остов графа.
Якщо | Xp | <n, то перейти до кроку 2.
Контрольний приклад
Для прикладу розглянемо граф, зображений на рисунку 8.3.
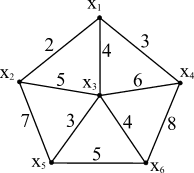
Знайдемо для нього найкоротше остове дерево, використовуючи для цієї мети розглянутий вище алгоритм Прима-Краскала. Позначимо множину суміжних вершин, що не входять в породжене піддерево, як Г * (Xp). Таким чином, для всіх вершин, що входять у цю множину, оцінка β (xj) = 0, ∀ xj ∈ Г *(Xp). Вектор B є множина оцінок β (xi) для всіх вершин графа G: ∀xi ∈ X.
Довжина породженого піддерева позначається як L.
Ітерація 1: Xp = {x1}; Ap = ∅; Г *(Xp)={x2, x3, x4}; c (x1, x2 *) = 2; B = {1,1,0,0,0,0}, L = 2.
Ітерація 2: Xp = {x1, x2}; Ap = {(x1, x2)};
Г * (Xp) = {x3, x4, x5}; c (x1, x4 *) = 3;
B = {1,1,0,10,0}, L = 2 +3 = 5.
Ітерація 3: Xp={x1, x2, x4};Ap={(x1,x2);(x1,x4)};
Г * (Xp) = {x3, x5, x6}; c (x1, x3 *) = 4;
B = {1,1,1,1,0,0}, L = 5 +4.
Ітерація 4: Xp = {x1, x2, x3, x4}; Ap = {(x1, x2); (x1, x4); (x1, x3)};
Г * (Xp) = {x5, x6}; c (x3, x5 *) = 2; B = {1,1,1,1,1,0}, L = 9 +3 = 12.
Ітерація 5: Xp = {x1, x2, x3, x4, x5}; Ap = {(x1, x2); (x1, x4); (x1, x3); (x3, x5)};
Г * (Xp) = {x6}; c (x3, x6 *) = 4; B = {1,1,1,1,1,1}, L = 12 +4 = 16.
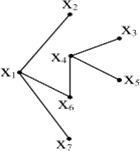
Задачу вирішено. Отримані множини вершин Xp і ребер Ap складають найкоротше остове дерево:
Xp = {x1, x2, x3, x4, x5, x6};
Ap = {(x1, x2); (x1, x4); (x1, x3); (x3, x5); (x3, x6)};
Сумарна довжина найкоротшого остового дерева L = 16.
Результат рішення задачі представлений на рисунку 8.4.
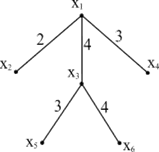
Порядок виконання роботи
1. Одержати завдання у викладача у вигляді початкового неорієнтованого графа.
2. Скласти блок-схему програми, що визначає найкоротше остове дерево графа за допомогою алгоритму Прима - Краскала.
3. Створити програму, що реалізує алгоритм Прима - Краскала. Початковий граф задається у вигляді матриці суміжності, що вводиться пострічково за допомогою консолі. Програма повинна вивести список ребер, що входять в найкоротше остове дерево.
Контрольні питання
1. Дайте визначення дерева, орієнтованого дерева.
2. Яке дерево називається остовом ?
3. Властивості остовів дерев. Теорема Келі.
4. Що називається коренем дерева?
5. Як перетворити неорієнтоване дерево в орієнтоване?
6. Скільки ребер містить остов дерева графа?
7. Задача знаходження найкоротшого каркасу графа.
8. Наведіть практичні приклади знаходження найкоротшого каркасу графа.
9. Реалізація алгоритму Прима - Краскала для знаходження найкоротшого остова графа.
ЛАБОРАТОНА РОБОТА № 9. РОЗФАРБУВАННЯ ГРАФА
Мета: Вивчення способу правильної розмальовки графа на основі евристичного алгоритму.
Теоретичні відомості: Різноманітні завдання, що виникають при плануванні виробництва, складанні графіків огляду, зберіганні і транспортуванні товарів і т.д., можуть бути представлені часто як задачі теорії графів, тісно пов'язані з так званою "задачею розмальовки". Графи, що розглядаються в лабораторній роботі, є неорієнтованими і не мають петель.
Граф G називають r-хроматичним, якщо його вершини можуть бути розфарбовані з використанням r кольорів (фарб ) так, що не знайдеться двох суміжних вершин одного кольору. Найменше число r, таке, що граф G є r - хроматичним , називається хроматичним числом графа G і позначається g(G). Задача знаходження хроматичного числа графа називається задачею про розфарбовування (або задачею розмальовки ) графа. Відповідна цьому числу розфарбування вершин розбиває множина вершин графа на r підмножин, кожна з яких містить вершини одного кольору. Ці множини є незалежними, оскільки в межах однієї множини немає двох суміжних вершин.
Задача знаходження хроматичного числа довільного графа була предметом багатьох досліджень наприкінці XIX і в XX столітті. З цього питання отримано багато цікавих результатів .
Хроматичне число графа не можна знайти, знаючи тільки числа вершин і ребер графа. Недостатньо також знати ступінь кожної вершини, щоб обчислити хроматичне число графа. При відомих величинах n ( число вершин), m ( число ребер ) і deg ( x1 ), ..., deg ( xn ) (степінь вершин графа) можна отримати тільки верхню і нижню оцінки для хроматичного числа графа.
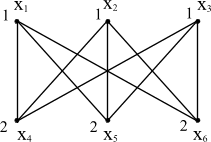
Приклад розмальовки графа показано на рисунку 9.1 . Цей граф є однією із заборонених фігур, використовуваних для визначення планарності. Цифрами " 1 " і " 2 " позначені кольоривершин.
Максимальне число незалежних вершин графа a(G), рівне потужності найбільшої множини попарно несуміжних вершин, збігається також з потужністю найбільшого множини вершин в G, які можуть бути пофарбовані в один колір, отже:
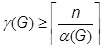 ,
,
де n - число вершин графа G, а[x] позначає найбільше ціле число, яке не перевищує x.
Ще одна нижня оцінка для g (G) може бути отримана таким чином:
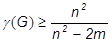 ,
,Верхня оцінка хроматичного числа може бути обчислена за формулою:
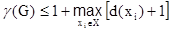 ,
,
Застосування оцінок для хроматичного числа значно звужує межі рішення. Для визначення оцінки хроматичного числа також можуть використовуватися інші топологічні характеристики графа, наприклад, властивість планарності.
Граф, який можна зобразити на площині так, що ніякі два його ребра не перетинаються між собою, називається планарним.
Теорема про п'ять фарб . Кожен планарний граф можна розфарбувати за допомогою п'яти кольорів так, що будь-які дві суміжні вершини будуть пофарбовані в різні кольори, тобто якщо граф G - планарний, то g (G) ≤ 5 .
Гіпотеза про чотири фарби (недоведена) . Кожен планарний граф можна розфарбувати за допомогою чотирьох кольорів так, що будь-які дві суміжні вершини будуть пофарбовані в різні кольори, тобто g (G) ≤ 4, якщо граф G - планарний.
У 1852 р. про гіпотезу чотирьох фарб говорилося в листуванні Огюста де Моргана з сером Вільямом Гамільтоном. З тих пір ця "теорема" стала, поряд з теоремою Ферма, однієї з найвідоміших невирішених задач в математиці.
Повний граф Gn завжди розфарбовується в n кольорів, що дорівнює кількості його вершин.
Евристичний алгоритм розфарбовування
Точні методи розмальовки графа складні для програмної реалізації. Однак існує багато евристичних процедур розфарбовування, що дозволяють знаходити хороші наближення для визначення хроматичного числа графа. Такі процедури також можуть з успіхом використовуватися при розфарбовуванні графів з великим числом вершин, де застосування точних методів не виправдане з огляду високої трудомісткості обчислень.
З евристичних процедур розмальовки слід відзазначити послідовні методи, засновані на упорядкуванні множинаі вершин.
В одному з найпростіших методів вершини спочатку розташовуються в порядку зменшення їх степенів. Перша вершина забарвлюється в колір 1 ; потім список вершин проглядається за спаданням степенів і в колір 1 забарвлюється кожна вершина, яка не є суміжною з вершинами, забарвленими в той же колір. Потім повертаємося до першої в списку незафарбованої вершини , зафарбуємо її в колір 2 і знову переглядаємо список вершин зверху вниз, фарбуючи в колір 2 будь-яку незабарвлену вершину, що не з'єднана ребром з іншою , вже пофарбованої в колір 2 вершиною. Аналогічно діємо з кольорами 3, 4 і т. д., поки не будуть пофарбовані всі вершини. Число використаних кольорів буде тоді наближеним значенням хроматичного числа графа.
Евристичний алгоритм розмальовки вершин графа має такий вигляд:
Крок 1. Сортувати вершини графа за степенями спадання:
deg ( xi ) ≥ deg ( xj ), ∀ xi , xj ∈ G ; Встановити поточний колір p = 1 ; i = 1.
Крок 2. Вибрати чергову НЕ розфарбовану вершину зі списку і призначити їй новий колір : col ( xi ) = p ; Xp = { xi }.
Крок 3. i = i + 1. Вибрати чергову НЕ розфарбовану вершину xi і перевірити умову суміжності: xi &∩; Г ( Xp ) = ∅ , де Xp - множина вершин, вже розфарбованих в колір p. Якщо вершина xi не є суміжною з даними вершинами, то також присвоїти їй колір p : col ( xi ) = p.
Крок 4. Повторити п.3, поки не буде досягнутий кінець списку (i = n).
Крок 5. Якщо всі вершини графа розфарбовані, то - кінець алгоритму;
Інакше: p = p + 1 ; i = 1. Повторити п.2.
Контрольний приклад
Розфарбуємо граф G, зображений на рисунку 9.2.
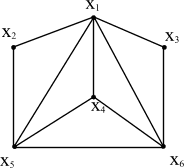
Проміжні дані для вирішення задачі будемо записувати в таблицю. Відсортуємо вершини графа за спаданням їх степенів. У результаті виходить вектор відсортованих вершин X * = {x1, x5, x6, x4, x2, x3}.
Відповідні даним вершинам степені утворюють другий вектор:
D = {5, 4, 4, 3, 2, 2}. У першому рядку таблиці запишемо вектор X *; в другій - вектор D. Наступні рядки відображають зміст вектора розмальовки col (X *).
Таким чином, даний граф можна розфарбувати не менш ніж у чотири кольори, тобто g (G) = 4.
| Номера вершин X* | x1 | x5 | x6 | x4 | x2 | x3 |
| Степени вершин D | 5 | 4 | 4 | 3 | 2 | 2 |
| p = 1 | 1 | – | – | – | – | – |
| p = 2 | 1 | 2 | – | – | – | 2 |
| p = 3 | 1 | 2 | 3 | – | 3 | 2 |
| p = 4 | 1 | 2 | 3 | 3 | 3 | 2 |
Порядок виконання роботи
1. Одержати завдання у викладача у вигляді початкового неорієнтованого графа :
2. Скласти блок-схему програми, що виконує розмальовку графа за допомогою евристичного алгоритму.
3. Створити програму, що реалізує евристичний алгоритм розмальовки графа. Вихідний граф задається у вигляді матриці суміжності, що вводиться через рядок за допомогою консолі. Програма повинна вивести список отриманих кольорів для всіх вершин графа.
Контрольні питання
1. Сформулюйте завдання розмальовки графа.
2. Який граф називається r - хроматичним?
3. Що називається хроматичним числом графа?
4. Як визначаються нижня і верхня оцінки хроматичного числа?
5. Який граф називається планарним ? У скільки кольорів можна його розфарбувати?
6. У скільки кольорів можна розфарбувати повний граф?
7. Евристичний алгоритм розмальовки графа.
9. Реалізація евристичного алгоритму для знаходження хроматичного числа графа.
ПЕРЕЛІК ПОСИЛАНЬ
1. Дискретна математика: Підручник / Ю. М. Бардачов, Н. А. Соколова, В. Є. Ходаков; за рец. В. Є. Ходакова. - 2-ге видання, переробл. і доповн. – К.: Вища школа., 2007. – 383 с. ISBN 978-966-642-343-9
2. Прикладная теория цифровых автоматов: учебн. для вузов по спец. ЭВМ / А. Я. Савельев. - М.: Высш. Школа, 1987. – 272 с.
3. Комп’ютерна дискретна математика: Підручник / М. Ф. Бондаренко, Н. В. Білоус, А. Г. Руткас. - Харків: «Компанія СМІТ», 2004. – 480 с. ISBN 966-8530-20-9
4. Комбинаторика для программистов: В.Липский – Пер. с польского. – М.: Мир, 1988. - 216 с.
5. Основы дискретной математики: Учеб. пособие для вузов / В. А. Горбатов. – М.: Высшая школа, 1986. - 311 с.
6. Теория графов. Алгоритмический подход / Н. Кристофидес. – М.: Изд. Мир, 1978, 432 с. - ISBN 5-330-00636-8
