ТЕМА 3.
Системи числення.
[ Попередня глава ]
[ Зміст]
[ Наступна глава ]
Під системою числення розуміють сукупність прийомів назви і позначення (запису) чисел. Умовні знаки, що використовуються для позна-чення чисел називають цифрами. Крім цифр використовуються також розділювачі (+,– , , , . і інші). Як і звичайна мова, мова чисел має свій алфавіт. Загальноприйнятою мовою чисел стала десятична система числення. Будь–яке число в ній подається за допомогою набору з десяти цифр: 0,1,2,3,4,5,6,7,8,9. Значення кожної цифри в запису числа залежить від позиції, яку вона займає в числі. Так, наприклад, в запису 555,5 цифра 5 зустрічається чотири рази, але в кожній позиції вона має різний сенс: крайня ліва цифра 5 означае кількість сотен і має значення 500, наступна цифра 5 означає кількість десятків, 5, яка стоїть перед комою, означає кількість одиниць і, нарешті, цифра 5 після коми – кількість десятих частин одиниці. Десятична система числення є позиційною.
Позиційная система числення – це система, в якій при запису чисел одна і та ж цифра має різні значення в залжності від позиції, яку вона займає в числі. В будь–якій позиційній системе числення використовується певна кількість різних цифр (символів) для позначення чисел. Тому вони відрізняються своїм базисом і основою.
Базис системи числення – набір різних цифр, що використовується для напису чисел в даній системі. Кількість цифр в базисі називається основою системи числення.
Позиційні системи числення називаються відповідно своїй основі: десятична – основа 10, вісімкова – основа 8, двійкова – основа 2. Можуть бути системи числення, що використовують більше 10 цифр. Наприклад, в шістнадцятковій системі числення використовуються шістнадцять цифр.
Широке розповсюдження десятичної системи числення, пов’язане з фізіологічною будовою рук (ніг) людини (10 пальців на руках (ногах)). Була б у нас дюжина (12) пальців на руках, то, наймовірніше за все ми б користувалися дванадцятирічною системою.
Оскільки за основу позиційної системи числення можна взяти будь–яке ціле додатне число більше одиниці, то таких систем можно створити дуже багато.
Для оцінки потрібності тієї чи іншої системи числення в якості основи для конструювання обчислювальної машини має значення, окрім простоти здійснення арифметичних операцій в ній, також і те, що зазвичай називають економічністю системи. Під цим розуміють множину чисел, які можна записати в даній системі за допомогою певної кількості знаків. Щоб в десятковій системі числення записати 1000 чисел (від 1 до 999), необхідно 30 знаков (по 10 цифр для кожного разряду). А в двійковій системі за допомогою 30 знаков можна записати 215 різних чисел (оскільки для кожного двійкового розряду потрібні тільки знаки 0 і 1, то за допомогою 30 знаків можна записати числа, що містять до 15 двійкових розрядів). Але 2 15 >1000, тому, маючи 15 різних розрядів, можна записати більше різних чисел, ніж за допомогою трьох десятичних розрядів. В загальному випадку, якщо взяти n знаків, а за основу системи числення прийняти деяке число x, то кількість розрядів визначиться як (n / x) розрядів, а кількість чисел, що при цьому можна записати, буде дорівнювати xn/x. Розглянемо цей вираз як функцію змінної x. Максимум цієї функции досягається при x = 2,718281828459045…. Це число є основою натуральних логарифмів, але воно не є цілим. Найближчими цілими до цього числа будуть 3 і 2. В силу простоти технічної реалізації імітування цифр двійкової системи (0, 1) в ЕОМ найбільш часто використовується двійкова система числення, відомі також реалізації ЕОМ з трійковою системою числення, наприклад, «Сетунь», створену в МДУ.
Щоб визначити, в якій системі числення записане число, її основу записують внизу після числа. Наприклад, 70810 , 368 , 1012.
В будь–якій позиційній системі числення її основа записується як 10, тобто одиниця в старшому розряді і 0 в молодшому.
Всі позиційні системи числення будуються по одному загальному принципу : вибираеться деяке ціле додатне число Р > 1 – основа системи числення; запис будь–якого числа М подається у вигляді полінома, тобто комбінації ступенів основи системи числення Р з коефіцієнтами а0, а1, а2, …, аk , що приймають значения від 0 до Р–1, тобто з базиса системи числення:
Якщо при записі числа відкинути ступені основи системи числення, то число можна записать в такому компактному вигляді:
Компактність подання чисел, а також зручні алгоритми виконання операцій додавання, множення, обумовили широко розповсюдження позиційних систем числення.
Непозиціні системи числення побудовані інакше. Наприклад, в системі римских цифр є набір символів: одиниця I , п’ять V , десять X , п’ятьдесят L і т.д., комбінація яких дозволяє подати будь–яке число. Так, число 77 в цій системі числення запишеться так:LXXVII. В цій системі значенння кожного символа не залежить від того місця, на якому він стоїть. В наведеному записі числа 77 цифра X використовується 2 рази, і кожен раз означає одну и ту ж величину – десять одиниць.
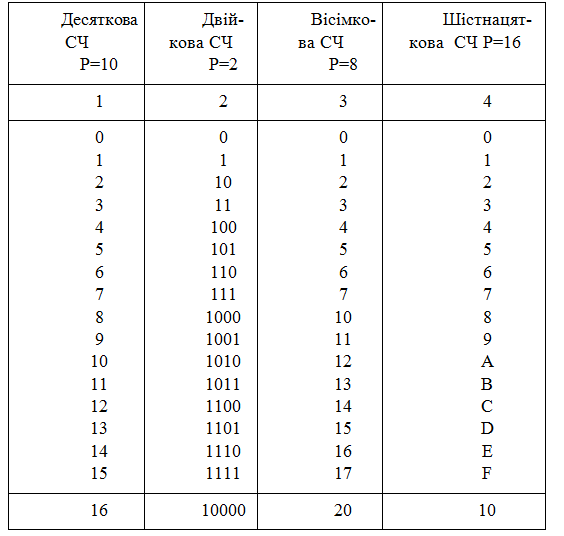
Один з перших творців електронних обчислювальних машин професор Атанасов А. запропонував використати в ЕОМ двійкову систему числення. Набір символом, що використовуються для подання і обробки інформації в комп’ютері найменший. Він включає всього два символи – 0 і 1, за допомогою комбінації яких (послідовностей одиниць і нулів) можна записати будь–яке число, причому, при цьому може знадобитися різна кількість битів (двійкових розрядів), що вказано в таблиці 1. Використання в сучасних ЕОМ двійкового подання інформації, як було відзначено раніше, пояснюється зручністю технічної реалізації пристроїв зберігання і обробки інформації.
Таблиця 1 – Зображення чисел в позиційних системах числення, що використовуються в комп'ютерах.
2.1 Переведення чисел з однієї системи числення в іншу.
При розвязанні задач на ЕОМ початкові дані зазвичай задаються в десятичной системі числення; в цій системе, как правило, нужно отримати і результат розвязку задачі. Але якщо ЕОМ працює в будь–якій іншій системі числення, наприклад в двійковій, то виникає потреба переведення чисел з однієї системи числення в іншу. Розглядаючи правила такого переведення обмежимося тільки такими системами числення, в яких базисними числами є цілі числа від 0 до P – 1 включно, де P – основа системи числення.
При переведенні числа з десяткової системи числення в систему числення з основою Р переведення цілої і дробової частин числа проводиться окремо.
Переведення цілого числа з десяткової системи числення в будь–яку іншу з основою Р проводиться багатократним діленням десяткового числа на основу Р, поки частка не стане менше Р. Остання частка буде старшим розрядом числа, а залишок від першого ділення на Р – молодшим.
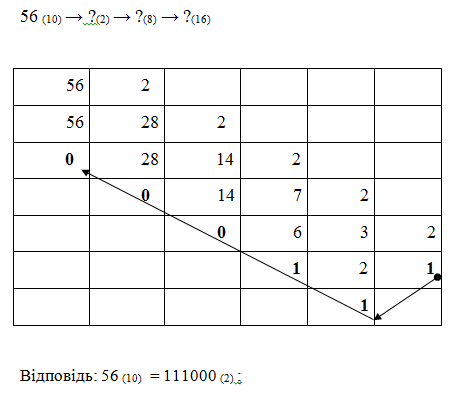
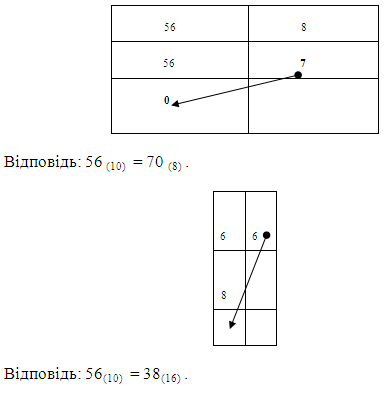
На практиці зручно користуватися схемой переведення, яку проілюструємо на прикладі переведення числа 56 з десяткової системи числення в двійкову, вісімкову і шістадцяткову:
Щоб перевести правильний дріб з десяткової системи числення в будь–яку іншу з основою P, її послідовно множать на P, при цьому кажен раз множиться тільки дробова частина утвореного добутку. Процес переведення продовжується або до достягнення заданої точності, або до знаходження періоду. Дріб в системі числення з основою P записується у вигляді дробу з цілих частин утворених добутків, починаючи з першого.
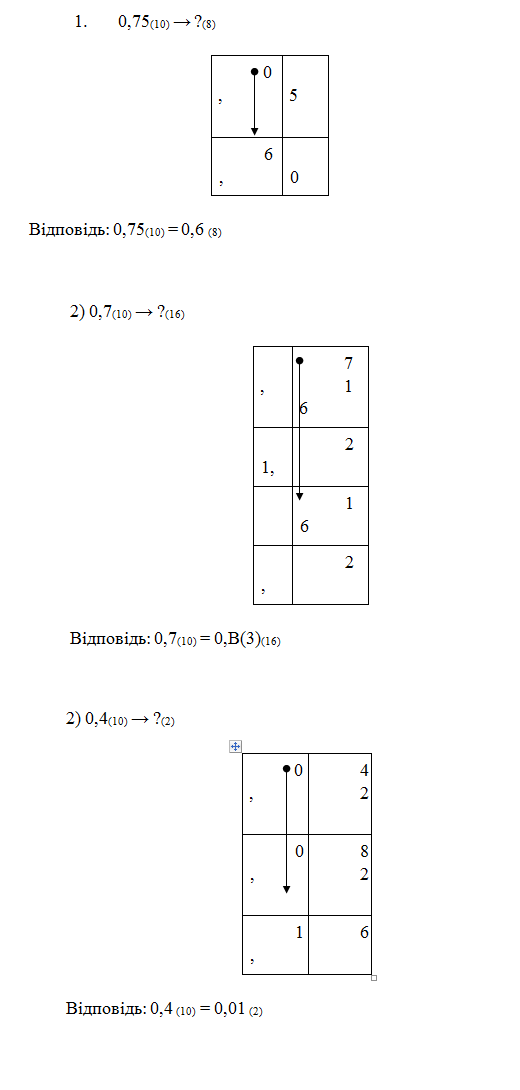
Переведення десяткових дробів зручно виконувати по схемі, яку покажемо на прикладах.
Приклад 1.
Перевести числа з однієї системи числення в іншу:
2.2 Розглянемо випадки переведення чисел з однієї системи числення в іншу, коли основи систем числення є ступенями двійки.
Оскільки основа вісімкової системи 8 = 23, то розкладення числа по ступеням 8 легко переводиться в розкладення по ступеням 2 і навпаки. При цьому кожна цифра вісімкової системи (0, …, 7) має своє розкладення по ступеням 2. Наприклад,
2(8) =0•2 2 +1•2 1 +0•2 0 =(010) 2 6 (8) =1•2 2 +1•2 1 +0•2 0 =(110) 2.
Тоді переведення з вісімкового подання числа в двійково–вісімкове здійснюється шляхом заміни кожної вісімкової цифри? що відповідає двійковій тріаді.
720 (8) =7•8 2+2•8 1+0•8 0 =(1•2 2+1•2+1•2 0 )2 6+(0•2 2+1•2+0•2 0 )•2 3+(0•2 2+0•2 1+0•2 0 )=1•2 8+1•2 7+1•2 6+0•2 5+1•2 4+0•2 3+0•2 2+0•2 1+0•2 0=111010000 (2)=111 010 000 (2).
Для подання двійкового числа в вісімковій системі треба число розбити на двійкові триади вліво і вправо від коми і потім замінити кожну триаду, відповідною їй вісімковою цифрою.
101 111 011, 001 100 (2) = 573,14 (8)
Чотири двійкових розряди дозволяють закодувати будь–яку десяткову цифру і отримати 16 різних кодових комбінацій, з яких 10 (от 0000 до 1001) використовуються для подання десяткових цифр. Кодові комбінації, що відповідають числам 10 і більше, умовно позначаються першими буквами латинського алфавіту (стовпчик 4 таблиці 1). Так отримується шістнадцяткова система числення. В программах для ЕОМ, щоб не записувати довгий ряд нулів і одиниць, замість кожних чотирьох розрядів (тетрад) записується їх шістнадцятковий еквівалент. Наприклад, шістнадцятковий еквівалент числа 0101 0001 1111 0011 буде 51F3.
Переведення числа, записаного в системі числення P, в десяткову систему виконується з урахуванням ваги кожного розряду або шляхом запису числа в вигляді розглдення по ступеням основи P . Наприклад,
- 1101(2) → ?(10)
1101(2) =1• 10 3 + 1• 10 2 + 0•10 1 + 1• 10 0 (2) →
1•8+1•4+0•2+1 (10) =13 (10) ;
або по схемі:
двійкове число 1 1 0 1 (2) десятичне число
8 4 2 1
1х1 = 1
0х2 = 0
1х4 = 4
1х8 = 8
Відповідь: 13 (10) - 354,4 (8) =3•8 2 +5•8 1 +4•8 0 +4•8 –1 (10) = 192+40+4+0,5 (10) =236,5 (10) ;
- A1F,8 (16) =A •16 2 +1•16 1 + F•16 0 +8•16 –1 (16) = 10•16 2 +1•16+15+8/16 (10) = 2591,5 (10) .
В другому випадку переведення виконується з урахуванням ваги кожного розряду.
2.3 Арифметичні операції в електронних обчислювальних маши-нах.
В обчислювальних машинах вся інформація подається в двійкової формі, а для виконання обчислювань використовується безпосередньо двійкова система числення.
Арифметичні операції з двійковими числами виконуються так же, як з десятковими, з тією лише різницею, що в десятковій системе цифри каждого разряда возрастают в порядке 1, 2, …, 8, 9, а при досягненні величини 10 в цьому розряді записується 0 і робиться перенесення одиниці в старший розряд. В двійкової системі використовуються тільки два символи 0 і 1, тому цифри в кожному розряді можуть зміноватися тільки в межах цих двох значень, післе цього відбувається перенесення в більщ старший розряд.
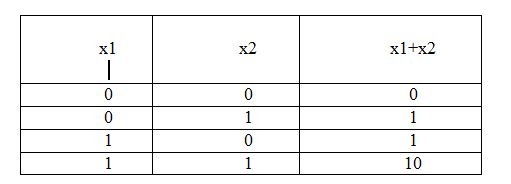
Тут 10 – це 2 в двійкової системе числення
Наприклад:
|
1110,01 (2) +1010,10 (2) 11000,11 (2) |
10111,011 (2) +11101,101 (2) 110101,000 (2) |
Зазвичай для подання додатних і від'емних чисел використовують величини зі знаками, причому при представленні додатних чисел знак «+» можна опускати, а знак «–» при відображенні від'емних чисел повинен ставитися, що для реалізації на обчислювальних машинах незручно. В обчислювальних машинах використовується форма подання чисел в доповняльних кодах, а знаки «+» і «–» використовуються для визначення арифметичних операцій.
В двійковій системі числення числа можуть бути подані в форме доповнення до основи системи числення, тобто до 2. В двійковому доповняльному коді всім додатним числам передує 0, а відемним числам – одиниця. Таким чином, при представленні чисел в доповняльному коді крайній лівий бит (старший) є знаковим: 0 означає додатне число, а 1 – від'ємне.
| 1011 –5 |
1100 -4 |
101 -3 |
110 -2 |
111 -1 |
000 0 |
001 1 |
010 2 |
011 3 |
0100 4 |
0101 5 |
Числа, що стоять по разні сторони від нуля, є взаємно доповняльними, тобто їх сума завжди дорівнює 0. Щоб подати двійкове число в доповняльній форме, його інвертують (заміняють 0 на 1, а 1 – на 0) прибавляють до нього 1 . Операція віднімання виконується шляхом додавання доповняльних кодів.
Приклад:
Виконати віднмання 10111,1 – 1010,1.
На першому етапі необхідно задані числа вирівняти по значності (вони повинні мати одинакову кількість розрядів) і подати в доповняльному коді.
[10111,1] доп.= 0 10111,1
[ –01010,1]доп.= 1 10101,0 + 00000,1 = 1 10101,1.
На другому етапі виконується віднімання як додання з доповняльним числом, тобто:
0 10111,1
+ 1 10101,1
01101,0 = 1101.
Операція множення, ділення, піднесення до степеня і обчислення функцій процесор не виконує, їх необхідно виконувати програмним шляхом, використовуюи зсуви вліво і вправо. Зсув двійкового числа на одну позицію вліво приводить до його подвоєння подобно тому, як зсув десяткового числа на одну позицію вправо – до його зменшення на 10. Зсув двійкового числа на одну позицію вправо ділить його на двоє.
Контрольні питання
- Що розуміють під системою числення?
- Чим відрізняється позиційна система числення від непозиційної?
- Дайте визначення базиса і основи позиційної системи числення.
- Як перевести число з 10→2, з 10→16?
- Як перевести число з 2→10, з 8→10, з 16→10?
- Який принцип побудови позиційних систем числення?
- Як відображаються числа в доповняльному коді?
- Опишіть схему віднімання чисел за допомогою доповняльного коду.
Завдання для самостійної роботи
-
Перевести числа з однієї системи числення в іншу:
625(10) → ?(2); 0,45(10) → ?(2); 3628,5(10) → ?(16); 0,6(10) → ?(8); 1024,4(10) → ?(8); 0,95(10) → ?(16); 134,6(8) → ?(10); 425,6(10) → ?(8); ВСО(16) → ?(10). 147,4(10) → ?(2); 5827,8(10) → ?(16). -
Записати числа в доповняльному коді:
а) 1563,04(10) г) –3А01(16) б) –2,149(10) д) –01010,101(2) в) –0,1001101(2) е) –37,54(8) -
Виконайте арифметичні операції в двійковій системі:
а) 1011,11 б) 1011,101 + 101,11 – 110,11
[ Попередня глава ] [ Зміст ] [ Наступна глава ]