ТЕМА 5.
Алгоритми. Визначення і властивості алгоритмів.

[ Попередня глава ] [ Зміст] [ Наступна глава ]

Широка популярність поняття алгоритма в наш час пояснюється развитком і широким використанням комп?ютерної техники. Використання ЕОМ сприяла тому, що розробка алгоритма – необхіднимий етап в процесі розвязання задачі на ЕОМ і що, в звязку з цим, алгоритми мають самостійну цінність як інтеллектуальние ресурси суспільства.

Понятття алгоритма виникло задовго до появи ЕОМ і стало одним з основних понять математики і належить до фундаментальних концепцій інформатики.

Слово «алгоритм» пішло від імені середньоазиатського (узбекського) математика аль–Хорезмі (IХ ст.) і використовувалось в математиці для позначення правил виконання чотирьох арифметичних дій: додавання, вціднімання, множення, ділення. В наш час понятття алгоритма використовується не тілько в математике. Його використовують в багатьох областях людської діяльності, наприклад говорять про алгоритм управління виробничим процесом, алгоритм гри в шахи, алгоритм користування побутовим приладом, алгоритм пошуку шляху в лабіринті, алгоритм управління польотом ракети и т.п.

Для тлумачення поняття «алгоритм» важливе значення має визначення поняття «виконавець алгоритму». Алгоритм формулюється в розрахунку на конкретного користувача, наприклад людину, специально дресирована тварина, особливу машину – автомат і т.д. Алгоритм є керівництвом до дій для виконавця, тому значення слова «алгоритм» близьке за змістом до значення слів «вказівка» або «предписание». Можна сказати, що алгоритм – зрозуміла і точна інструкція (вказівка) виконавцю здійснити певну послідовність дій для досягнення вказаноі мети або рішення поставленой задачі. Сказане не є визначенням в математичному сенсі, а лише відображає інтуітивне розуміння алгоритма, що склалося за довгі роки.

Приклад 1. Нехай є текст на російській мові, подготовлений спеціа-льним чином, що закінчується спеціальним символом @, що більше ниде в тексті не зустрічається Необхідно порахувати число голосних букв в заданому тексті.

Для розвязання цієї задачі можна запропонувати такий спосіб лічби числа голосних букв: читати послідовно символ за символом в кажен раз, коли черговий символ є голасна буква російського алфавиту, прибавляти до лічильника одиницю (передбачається, що виконавець цього алгоритму вміє розрізняти голосні і не голосні букви). Лічба починається з нуля і продовжується доти, поки не буде прочитаний символ @, що позначає кінець текста. Наведений вище опис дає лишє ідею алгоритму, але, щоб перетворити його в зрозумілу і точну інструкцію виконавцю, його необхідно уточнити.

По-перше, об?ектами алгоритму є символи тексту і числа. Над сим-волами тексту виконуються операції зчитування, пошуку наступного символа, порівняння символа с символом @ і порівняння символа з однією з голосних букв російського алфавиту. Над числами виконується операція додлавання одиниці.

По-друге, символи тексту читаються послідовно один за другим, починаючи з першого символа до символа @ включно. Щоб не помилитися при зчитуванні, передбачимо, що наш абстрактний виконавець має в своєму розпорядженні вказівник, який можна переміщувати по тексту і який вказує на черговий символ, що зчитується. Тому пошук наступного символа зводиться до переміщення вказівника на наступний по порядку символ тексту.

По-третє, лічба числа голосних букв починається з нуля, тому до початку работи лічильник числа голосних повинен бути обнуленим.

Враховуючи ці зауваження, сформулюємо алгоритм у вигляді такої послідовності дій:

  1. Записати в лічильник 0.
  2. Встановити вказівник на перший символ тексту.
  3. Якщо символ не є @, то перейти до п.4, інакше перейти до пункту 7.
  4. Якщо символ – голосна буква російського алфавиту, то збільшити лічильник на одиницю.
  5. Перевести вказівник на наступний символ тексту.
  6. Перейти до п.3.
  7. Взяти число, що знаходиться в лічильнику, як відповідь. Стоп.

Розглянемо основні особливості ( властивості ) алгоритму.

  1. Алгоритм має деяке число вхідних величин – аргументів , що задаються до початку работи (в наведеному вище прикладі вхідними даними є символи тексту і набір голосних букв).

    Мета виконання алгоритму – отримання результату ( результатів ), що має досить визначене відношення до початкових даних.

    В даному прикладі результат – число, що означає число голосних букв в початковому тексті.

    Для алгоритму можна брати різні набори вхідних даних, тобто. використовувати один и той же алгоритм для розвязання цілого классу однотипних задач, що відрізняються початковими даними. Цю властивість алгоритму називають масовістю. Розглянутий в прикладі алгоритм може бути застосований до різних текстів російською мовою. Разом з тим існують і такі алгоритми, які можуть бути застосовані тільки до единого набору початкових даних. Наприклад, для алгоритму користування автоматичним турнікетом при вході вметро існує единий варіант початкового даного – тридцяти копійковий жетон. Тому поняття масовості потребує уточнення. Можна вважати, що для кожного алгоритму існує свій клас об?єктів, допустимих в якості початкових даних. Тоді властивість масовості означає засосування алгоритму до усіх об?єктів цього классу. А кількість об?єктів классу (кінечне або безкінечне) – властивість самого класу початкових даних.

  2. Щоб алгоритм можна було виконати, він повинен бути зрозумілим виконавцю. Приведений в прикладі алгоритм лічби голосних букв може бути зрозумілим людині, яка знає українську мову. Щоб цей алгоритм міг бути також виконаний людиною, яка не знає українську мову, не-обхідно записати алгоритм на мові зрозумілій виконавцю, і повідомити йому додаткові відомості: перелічити явно голосні букви українського алфавіта.

    Зрозумілість алгоритму означає знання виконавця про те, що треба робити для виконання цього алгоритму.

    Таким чином, при формулюванні алгоритму необхідно враховувати можливості і особливості виконавця, на якого розрахований алгоритм.

  3. Алгоритм представлений у вигляді зліченої послідовності кроків. Кажуть, що алгоритм має дискретну структуру. Відповідно, його вико-нання розділюється на виконання окремих його кроків, виконання кожного наступного кроку починається після завершення попереднього.

  4. Виконання алгоритму закінчується після виконання зліченого числа кроків. При ввиконання алгоритму деякі его кроки можуть повторюватися багаторазово. В розглянутому вище прикладі багаторазово повторюються кроки з третього по шостий. Однак виконання алгоритму все ж завершиться за злічене число кроків, тому що текст мат злічену довжину і в ньому є символ @. При читанні цього символу буде виконано сьомий крок алгоритму, що завершує його виконання.

    В математиці існують обчислювальні процедури, що мають алгоритмічний характер, але не володіють властивістю конечності. Так, можна сформулювати процедуру обчислення числа ?. Така процедура описує безкінечний процес і николи не завершиться. Якщо ж її штучно перервати, наприклад ввести умовне завершения процесу обчислень вигляду: «Закінчити обчислення після отримання N десятичних знаків числа ?», то получиться алгоритм обчислення N десятичних знаків числа ?. На цьому принципі базується отримання багатьох обчислювальних алгоритмів: будується бескінечний процес, що сходиться до искомому розв'зку. Він переривається на деякому кроці, і отримане значення приймається за наближений розв'язок задачі, що розглядається. При цьому точність наближення залежить від числа кроків.

  5. Кажен крок алгоритму повинен бути чітко і однозначно визначений і не повинен допускати довільної трактовки виконавцем. При виконанні алгоритма виконавець повинен діяти чітко у вдповідності з його правилами і у нього не повинно виникати необхідності виконувати будь-які дії, відмінні від передбачених алгоритмом. Інакше, алгоритм розрахований на виключно механічне виконання . Ця дуже важлива особливість означае, зокрема, що якщо один и той же алгоритм доручити для виконання різним виконавцям, то вони прийдуть до одного і того ж результату, аби ці виконавці розуміли алгоритм. Саме визначеність алгоритму дає можливість доручити його виконання автомату, що не має «здорового глузду».

    B наведеному вище прикладі, дія переміщення вказівника на наступний символ достатньо точно визначено, якщо текст розташований на довгій вузькій стрічці і витягнуть в одну стрічку (наприклад, надрукований на вузькій телетайпній стрічці). Якщо ж текст розбитий на рядки і сторінки (тобто має складну структуру), то дія переміщення вказівника на наступний символ вже не є настільки очевидним. В цьому випадку необхідні інструкції, як діяти виконавцю, коли закінчиться черговий рядок або чергова сторінка тексту.

    Таким чином, формулювання алгоритму повинна бути настільки точним, щоб в повноті визначати всі дії виконавця.

  6. Кожен крок алгоритму повинен бити виконаний точно і за скінчений час. В цьому сенсі кажуть, що алгоритм повинен бути ефективним , тобто дії виконавця на кожному кроці виконання алгоритму повинні бути достатньо простими, щоб їх можна було виконати точно и за скінчений час. Тому, наприклад, інструкція вигляду: «Якщо будь–яке ціле число, більше 6, можна подати в вигляді суми трьох простих чисел, то лічиль-ник збільшиться на 1, інакше лічильник зменшиться на 1» – неефективно, так як не відомий спосіб доведення істинності або жибності твердження, що міститься в ньому. Отже, виконавець не може виконати цей крок алгоритму, поки не знайде відповідного доведення.

    Зазвичай окремі інструкції виконавцю, що містяться на кожному кроці алгоритму, називають командами. Таким чином, ефективність алгоритму пов'язана з можливістю виконання кожної команди за скінчений час. Виконавці відрізняються один від одного своїми можливостями, тобто репертуаром команд, які вони «розуміють» і можуть виконувати. Сукупність команд, які можуть бути виконані конкретним виконавцем, називається системою команд виконавця. Відповідно, алгоритм, розрахований на конкретного виконавця, повинен бути сформульований так, щоб містити тільки ті команди, які входять в систему команд цього виконавця.

Крім того, ефективність означає, що алгоритм може бути виконаний не просто за скінчене, а за обгрунтований скінчений час (важливо, щоб задача за розробленим алгоритмом розв'язувалася як можна швидше). Ось чому при розробці алгоритмів повинні враховуватися і можливості конкретних фізичних виконавців алгоритму.

Наведені вище коментарі пояснюють інтуітивне поняття алгоритму, але саме це поняття не стає від цього більш чітким і строгим. Однак математики тривалий час задовільнялися цим поняттям. Лише зі знайденням алгоритмічно нерозв'язуваних задач, тобто задач, для розвязання яких неможливо побудувати алгоритм, з'явилася певна необхідність в побудові формального визначення алгоритму, що відповідає відомому інтуітивному поняттю.

Інтуітивне поняття алгоритму в силу своєї нечіткості не может бить объектом математического изучения, поэтому для доказательства существования или не существование алгоритму розвязання задачі було необхідне чітке формальне визначення алгоритму.

Побудова такого формального визначення почалася з формалізації об'єктів (операндів) алгоритму, так як в інтуітивному понятті алгоритму його об'єкти можуть мати довільну природу. Ними можуть бути, наприклад, числа, показники датчиків, що фіксують параметри виробничого процесу, шахматні фігури і позиції і т.д. Однак, передбачаючи, що алгоритм має справу не з самими реальними об'єктами, а з їх зображеннями, можна вважати, що операнди алгоритму є слова в довільному алфавіті. Тоді получается, що алгоритм перетворює слова в довільному алфавіті в слова того же алфавіту. Подальша формалізація поняття алгоритму пов'язана з формалізацією дій над операндами і порядку цих дій. Одна з таких формалізацій була запропонована английским математиком А.Тьюрінгом в 1936 році, який формально описав конструкцию деякої абстрактної машини (машини Тьюрінга) як виконавця алгоритму і висловив тезіс про те, що будь-який алгоритм може бути реалізований відповідною машиною Тьюрінга.

Будемо притримуватися неформального визначення алгоритму, що формулюється наступним чином:

Алгоритм – це впорядкована послідовність вказівок, виконання якої приводить від початкових даних до бажаного результату.

Іншими словами алгоритм це план розв'язання задачі, записаний у вигляді послідовності вказівок чи груп вказівок.

Розглянемо приклад алгоритму Евкліда, виконуючи який визнача-ється спільний найбільший дільник двох додатних цілих чисел a і b .

Приклад 2. Алгоритм Евкліда, знахождення найбільшого спільного дільника двох додатних чисел.

  1. Перевірити a > b. Якщо так, то перейти до вказівки 2, інакше – до вказівки 3.
  2. Взяти за нове значение a різницю a – b. Перейти до вказівки 1.
  3. Перевірити b > a . Якщо так, то перейти до вказівки 4, инакше – до вказівки 5.
  4. Взяти за нове значення b різницю b – a, перейти до вказівки 1.
  5. За результат взяти останнє значення a( b ). Перейти до вказівки 6.
  6. Закінчити процес.

В наведеному вище алгоритмі, передбачається, що його може виконати будь–яка людина або обчислювальна машина, яка вміє виконувати операціїи порівняння і віднімання двох чисел. Нагадаємо, що в школі найбільший спільний дільник визначається як добуток спільних простих дільників чисел. В даному алгоритмі про добуток і поняття дільника числа немає навіть нагадування і, тим неменше, слідуючи йому, завжди визначається найбільший спільний дільник двох цілих додатних чисел. Цей факт говорить про те, що отримати результат можна різними способами з використанням операцій, які, на перший погляд, не мають до розв’язуваної проблеми ниякого відношення, що дозволяє серед всіх можливих варіантів розв'язання задачі, шукати найбільш ефективний. В подальшому розглядаються алгоритми для обчислювальних машин. Сучасні комп'ютери з потужним програмним забезпеченням можуть виконувати різні операції: від простих арифметичних операцій, що виконуються над двомя числами до розв'язання складних задач з багатьох сфер діяльності людей. Якщо на комп'ютері є програма, що дозволяє розвязати необхідну задачу, то алгоритм розвязання такої задачі зводиться до опису процесу введення початкових даних, звернення до необхідної програми і отримання результатів в необхідному вигляді. Одночасно для дуже багатьох простих задач немає готових програм для їх розвязання. Не можна на всі випадки, да і не має такої необхідності, зберігатиь в пам'яти потрібні програми. Але практично усі програмні системи, що використовуються на комп'ютерах, мають реалізовані мови програмування. Вони дозволяють з невеликими затратами склати самостійно програму озвязання досить складних задач. Для реализації такої можливості треба вміти складати алгоритми і знати правила (синтаксис) запису вказівок на алгоритмічній мові. В подальшому передбачається, що «машина вміє» виконувати усі арифметичні операції, операції порівняння, логічні операції, а також може обчислювати практично всі елементарні функції. Крім того вона может ввести в пам'ять необхідні дані, а також надрукувати або вивести на монітор комп’ютера відповідні результати.

Таким чином, алгоритми повинні мати такі основні властивості: масовість (результативність); понятність; дискретність; конечніс-ть; визначеність; ефективність.

Серед інших властивостей алгоритмів, треба відзначити оптимальність і елегантність. Однак поняття оптимальності в алгоритмах має компромісний характер, оскільки можна оптимізувати кількість необхідимих для отримання результату операцій, або обсяг необхідної пам'яти, або швидкість виконання і навіть понятність алгоритму. Тому, складаючи алгоритм, треба визначитися, що треба оптимізувати в першу чергу і як цього досягти. Розробка алгоритмів є не тільки трудомістким процесом, але в деякому розумінні мистецтвом, тому так цінні елегантні алгоритми. Розробка алгоритма передбачає від розробника наступного:

Види и способи запису алгоритмів

Розрізняють три основних види алгоритмів:

  1. лінійні;
  2. розгалужені;
  3. циклічні.

Алгоритм називається лінійним, якщо його вказівки виконуються послідовно в тому порядку, в якому вони записані.

Алгоритм ? розгалужений, якщо в процесі розвязання треба перевіряти деякі умови і в залежності від їх виконання чи невиконання, виконуються ті або інші групи вказівок.

Алгоритм – циклічний, якщо в ньому є хоча б одна група вказівок, що в процесі виконання повторюється.

Для реальних задач, як правило, алгоритми мають всі три види, тобто в них використовуються і лінійні групи вказівок, і розгалужені участки, і циклічні групи. Існує декілька способів запису алгоритмів, що використовуються при розробці програм для розвязання задач на ЕОМ:

Блок-схема алгоритму

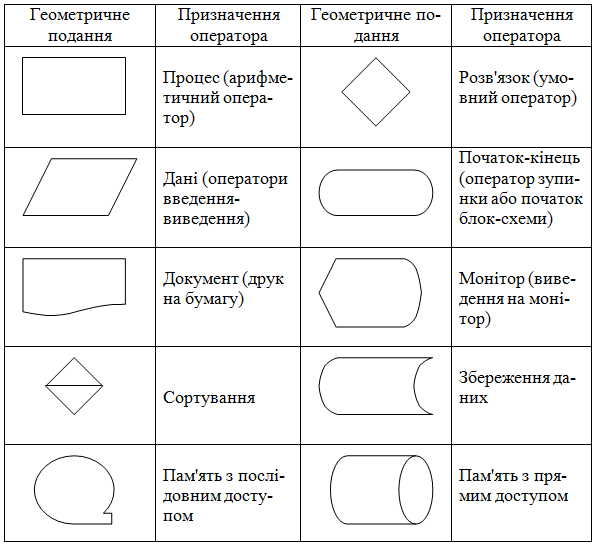
Блок-схемою алгоритму називається геометричне подання операторної схеми алгоритма, в якому оператори відображаються у вигляді геометричних фігур, а послідоність їх виконання вказується стрілками.

При побудові блок-схеми алгоритма прийнята стандартна система геометричних фігур, що використовуються для різних видів операторів. В таблиці 1 приведені основні оператори і їх геометриче подання, що відповідає прийнятому стандарту.

Для реальних задач, як правило, алгоритми бувають трьох видів, тобто в них існують і лінійні групи вказівок, і розгалужені ділянки, і циклічні групи. Існує декілька способів запису алгоритмів, які використовуються при розробці програм для розвязання задач на ЕОМ:

Контрольні питання

  1. Що розуміють під визначенністю алгоритма?
  2. Чи мають значущість алгоритми, що не мають властивості масовості? Чому?
  3. Які бувають види алгоритмів ?
  4. Дайте визначення оператора и опишіть структурну класифікацію операторів.
  5. Опишіть класифікацію операторів за їх призначенням.
  6. Які оператори циклу існують?

    7. Таблиця 3 ? Основні оператори і їх геометрне подання, що відповідає прийнятому стандарту.

  7. Що таке операторна схема алгоритма?
  8. Що таке блок-схема алгоритма?
  9. Опишіть основні конструкції, що використовую при розробці блок-схем алгоритмів.

Завдання для самостійної роботи

Розробити алгоритми розв'язання наступних задач:

  1. Побудувати таблицю переведення температури з градусів по шкалі Цельсія (С) в градуси шкали Фаренгейта (F) для значень від 15°С до 30°С з кроком 1°С.(Переведення здійснюється по формулі F = 1,8C + 32.)

  2. В області 10 районів. Відомі площі, що засіваються пшеницею, і середня врожайність (ц/га) в кожному районі. Визначити кількість пшениці, що була зібрана в області і середню врожайність по області.

  3. Побудувати таблицю відповідності між вагою в фунтах і вагою в кг для значень від 1 до 10 фунтів з кроком 1 фунт (1 фунт = 400г).

  4. Розробити алгоритм, в якому визначається найменший елемент матриці А( n, m), а потім його значення віднімається від усіх елементів цієї матриці.

[ Попередня глава ] [ Зміст ] [ Наступна глава ]s