Розділ 2 МАТЕМАТИЧНІ МОДЕЛІ ЗАКОНІВ РОЗПОДІЛУ В ТЕОРІЇ НАДІЙНОСТІ
2.1 Залежність інтенсивності відмов від часу
Будь-який технічний засіб з початку і до кінця експлуатації має три найбільш характерних періоди роботи:
1) припрацювання (
);
2) нормальна експлуатація (
);
3) старіння чи знос (
) (рис. 2.1).
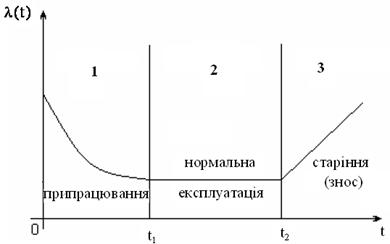
Рисунок 2.1 – Залежність інтенсивності відмов від часу роботи ТЗ
Період припрацювання характеризується високою інтенсивністю відмов, викликаних відхиленням від вимог конструкторсько-технологічної документації, що розподіляються за законом розподілу Вейбулла й усуваються за рахунок введення технологічного припрацювання («технологічного прогону»). Як видно з рис. 2.1 інтенсивність відмов на першому періоді монотонно зменшується.
Період нормальної експлуатації характеризується мінімальною і постійною інтенсивностями відмов. Ці відмови називаються раптовими, носять випадковий характер і розподіляються як правило за експоненціальним законом розподілу. Тут інтенсивність відмов залишається приблизно однаковою (див. рис. 2.1).
Період старіння або зносу характеризується різким збільшенням інтенсивності зносових відмов, що розподіляються за нормальним законом розподілу (законом Гаусса). На третьому періоді, як видно з рис. 2.1, інтенсивність відмов постійно зростає.
Виходячи з вище викладеного розглянемо детальніше найчастіше використовувані для розрахунку надійності ТЗ закони розподілу, що характеризують безперервні випадкові величини.
2.2 Розподіл Вейбулла
Розподіл Вейбулла (distributing of Veybulla) – двопараметричний закон розподілу випадкового напрацювання до відмови з параметрами: 
, що визначає масштаб, і k, що визначає асиметрію.
Показники надійності при такому законі розподілу будуть визначатися так:
, (2.1)
, (2.2)
, (2.3)
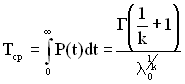, (2.4)
де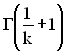 
– гамма-функція.
Гамма-функція визначається за виразом
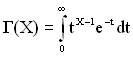. (2.5)
Характеристика зміни ймовірності безвідмовної роботи, що залежить від часу напрацювання при перерозподілі відмов за законом Вейбулла, подана на рис. 2.2.
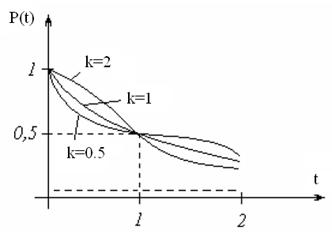
Рисунок 2.2 – Характеристика зміни ймовірності безвідмовної роботи для розподілу Вейбулла при k=2, k=1 та k=0.5
Дисперсія часу безвідмовної роботи для розподілу Вейбулла з урахуванням рівняння (1.12) описується виразом
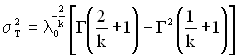. (2.6)
Отже, інтенсивність відмов 
, що розподілені за законом Вейбулла, при k < 1 – монотонно зменшується, при k >1 – монотонно збільшується і при k = 1 – 
= const (рис. 2.3).
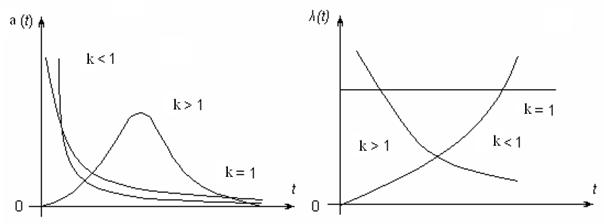
Рисунок 2.3 – Характеристики зміни частоти та інтенсивності відмов, що розподілені за законом Вейбулла
Приклад 2.1. Визначіть середнє напрацювання 
та інтенсивність відмов 
для ТЗ, час безвідмовної роботи якого розподілений за законом Вейбулла з параметрами k = 1.5, 
= 10-4год-1 за час роботи t = 100 год.
Розв’язування:
Для розрахунку скористаємося формулою (2.4) для розподілу Вейбулла
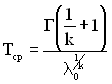=(10-4)-0,67Г(1,67).
Знайшовши з довідникової таблиці значення гамма-функції Г(1.67) = 0,9033 і провівши нескладні розрахунки, отримаємо = 418 год.
Підставляючи у формулу (2.3) параметри розподілу Вейбулла k і λ, розрахуємо інтенсивність відмов ТЗ за час t = 100 год.:
λ(100) = λk(100)k-1 = 1,5·10-3 год-1.
2.3 Експоненційний розподіл
Експоненційний закон розподілу – однопараметричний закон з постійною інтенсивністю відмов (λ0 = const). Він є частковим випадком розподілу Вейбулла при k = 1.
Ймовірність безвідмовної роботи, частота відмов і середнє напрацювання до відмови при експоненційному розподілі визначаються за формулами:
(2.7)
, (2.8)
. (2.9)
З виразу (2.3) випливає, що при k=1 інтенсивність відмов 
. Саме тому експоненційний закон визначається тільки одним параметром 
, що являє собою постійну інтенсивність відмов.
Замінюючи у виразі (2.7) на 1/Тср, отримаємо
. (2.10)
Ймовірність безвідмовної роботи на інтервалі часу t = Tcp при експоненційному розподілі дорівнює
.
Дисперсія часу безвідмовної роботи для експоненційного закону розподілу розраховується за формулою
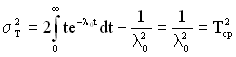. (2.11)
Графік зміни ймовірності безвідмовної роботи від часу при експоненційному розподілі відмов зображено на рис. 2.4.
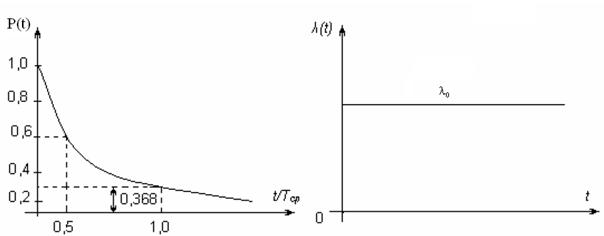
Рисунок 2.4 – Експоненційний розподіл ймовірності безвідмовної роботи та інтенсивності відмови
Знайдемо умовну ймовірність того, що для експоненційної моделі ТЗ пропрацює безвідмовно на інтервалі часу t, після того як він безвідмовно пропрацював на інтервалі Т. В цьому випадку маємо
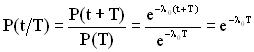. (2.12)
Звідси випливає важливий висновок: для експоненційного закону розподілу ймовірності безвідмовної роботи розподіл часу безвідмовної роботи не залежить від того, скільки часу ТЗ пропрацював до початку відліку від моменту першого ввімкнення. Інші закони розподілу такої властивості не мають, оскільки в інших розподілах 
, а залежить від часу.
Модель експоненційного розподілу широко використовується для апріорного аналізу надійності. При апріорному аналізі надійності необхідно проводити перевірку відповідності експоненційної моделі результатам випробувань.
Приклад 2.2. Напрацювання ТЗ до відмови описується експоненційним розподілом з параметром 
=10-4 год-1. Визначіть Р(t) i a(t) ТЗ за час роботи t = 2000 год., а також визначіть середнє напрацювання Тср.
Розв’язування:
Відповідно до формули (2.7) отримаємо
=0.819.
Відповідно до (2.8) отримаємо
год-1.
На основі рівняння (2.9) середнє напрацювання до відмови складає
год.
2.4 Розподіл Релея
При розподілі Релея ймовірність безвідмовної роботи на інтервалі (0; t) дорівнює
(2.13)
де r – параметр розподілу Релея, який одночасно є модою цього розподілу (рис. 2.5, а).
Мода неперервного розподілу – це точка максимуму щільності розподілу ймовірності а(t). Мода дискретного розподілу – це таке спектральне значення 
, при якому попереднє і наступне спектральні значення мають ймовірність, меншу ніж Р().
Щільність розподілу напрацювання до відмови дорівнює (рис. 2.5, б)
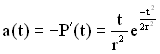. (2.14)
Інтенсивність відмов дорівнює (рис. 2.5, в)
. (2.15)
Середній час безвідмовної роботи Тср для розподілу Релея описується виразом
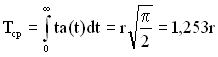. (2.16)
Відповідно дисперсія часу безвідмовної роботи описується виразом
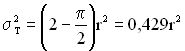. (2.17)
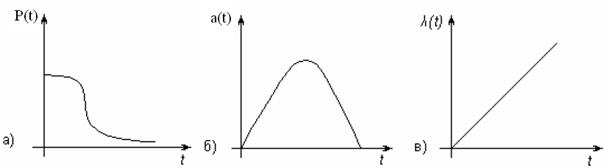
Рисунок 2.5 – Характеристики зміни ймовірності безвідмовної роботи, щільності розподілу напрацювання до відмови та інтенсивності відмови розподіленими за законом Релея
