3.3 Розподіл норм надійності по елементах

При розрахунку надійності ТЗ на першому етапі проектування (етап ескізного проектування) необхідно знайти значення ПН блоків і вузлів ТЗ за заданим в технічному завданні значенням ПН на весь ТЗ в цілому. При цьому вибір того або іншого способу розподілу норм надійності по блоках, функціональних вузлах і елементах багато в чому залежать від наявної у розробника інформації про ТЗ.

Існує чотири основні прийоми розподілу норм надійності:

1. За принципом рівнонадійності елементів;

2. З врахуванням існуючого співвідношення ПН елементів;

3. З врахуванням перспектив вдосконалення елементів;

4. З врахуванням вартості проектування, виробництва і експлуатації елементів.

Розглянемо всі ці способи розподілу норм надійності на прикладах.

Приклад 3.1

Проектується підсилювач з трьох рівнонадійних послідовних каскадів.

Задана вірогідність БР підсилювача має складати P(t) = 0,98 протягом часу t_ТЗ = 2000 год.

Визначіть значення λ_каск.(t) для кожного каскаду.

Розв’язування:

Приймаємо експоненціальну модель розподілу вірогідності БР:

.

Оскільки підсилювач складається з трьох рівнонадійних послідовних каскадів, то ПН для ТЗ в цілому будуть пов’язані такими співвідношеннями:

; ; ;

.

Враховуючи останній вираз, можна розрахувати інтенсивність ТЗ в цілому:

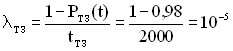(год)^-1.

Таким чином для одного каскаду інтенсивність має бути такою:

(год)^-1.

Приклад 3.2

1. Проектується ТЗ, що складається з трьох блоків A, B, C.

2. Задана вірогідність БР об'єкта складає P_ТЗ(t₁) = 0,97 протягом часу t₁ = 100 год.

3. Існує прототип, що складається з блоків A, B, C, кожний з яких характеризується інтенсивністю відмов відповідно:

год^-1; год^-1; год^-1.

Визначіть норми надійності у вигляді інтенсивності відмов λ для проектовних блоків А₁, В₁, С₁ λ_А1, λ_В1, λ_С1.

Розв’язування:

1. Враховуючи прототип, визначимо коефіцієнт, що враховує частку відмов проектуємого ТЗ через відмови j-го блока:

,

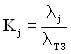де – відповідно інтенсивність відмов всього ТЗ та j- го блока.

Всі коефіцієнти K_j знаходять через співвідношення інтенсивностей відмов прототипу за формулою:

,

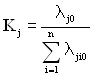де n – число елементів.

У нашому випадку:

;

;

.

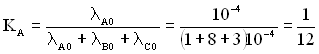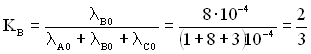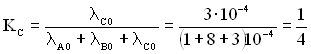2. Знайдемо значення λ(t) для проектовного ТЗ з виразу:

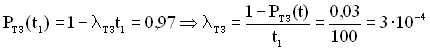(год)^-1.

3. Визначаємо норми надійності для блоків проектовного ТЗ:

(год)^-1;

(год)^-1;

(год)^-1.

Приклад 3.3

1. Проектовний ТЗ складається з двох послідовних блоків A1 і B1.

2. Задана вірогідність БР проектовного ТЗ складає P_ТЗ(t₁) = 0,97 протягом часу t₁ = 100 год.

3. Дата випуску проектовного ТЗ – 2010 р.

4. Зміна інтенсивності відмов за 1992 ÷ 2002 роки для блоків, аналогічних блокам A1 і B1, може бути за роками випуску апроксимована виразом:

,

де – інтенсивність відмови ТЗ, випущеного в 1992 році;

L – рік випуску блока.

Для блока A0: (год)^-1; (год)^-1.

Для блока B0: (год)^-1; (год)^-1.

Визначіть норми надійності для ПН блоків A1 і B1 у вигляді інтенсивності відмов і .

Розв’язування:

1. Екстраполюємо значення λ блоків прототипу до 2010

(год)^-1;

(год)^-1.

2. Аналогічно прикладу 3.2 визначимо коефіцієнт K_j і норми надійності:

;

;

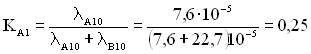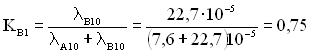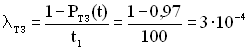(год)^-1;

(год)^-1;

(год)^-1.

Приклад 3.4

1. Система складається з чотирьох послідовних елементів 1, 2, 3, 4.

2. Значення параметрів відмов ТЗ ω_ТЗ = 10^-5 (год)^-1.

3. Час виробництва і проектування системи t=5 років, технічний ресурс t_р = 20 років.

4. Вкладення в одиницю часу (1 год.) проектування і виробництва елементів передбачаються постійними і для j-го елемента дорівнюють:

,

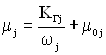де ω_j – параметр потоку відмов j-го елемента;

– витрати на одиницю часу на проектування і виробництво, що не залежать від надійності;

К_Гj – коефіцієнт готовності j-го елемента, значення якого такі:

=1,6·10^-4 (грн. · відмова)/год²; =3·10^-4 (грн. · відмова)/год²;

Витрати на одиницю часу зазвичай визначають на основі досвіду проектування аналогічних елементів, але в даному прикладі вони беруться рівними нулю ().

5. Поточні експлуатаційні витрати в одиницю часу постійні та дорівнюють:

,

де значення К_Е1=4·10⁶ грн/відмова; К_Е2= К_Е3= К_Е4=1,7·10⁶ грн/відмова, а значення .

6. Загальні витрати на проектування, виробництво і експлуатацію визначаються за формулою:

,

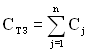де C_j – витрати на j-ий елемент;

n – число елементів в ТЗ.

Визначіть значення параметра потоку відмов для кожного елементу ТЗ ω_j.

Розв’язування:

Для порівняння витрат приводимо їх до одного моменту часу – початку експлуатації. Зведені експлуатаційні витрати обчислюємо за формулою:

,

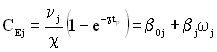де 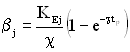, а .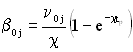

Виробничі витрати обчислюються за аналогічною формулою:

.

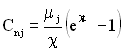Тому виробничі витрати можна обчислити з виразу

,

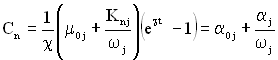де ; .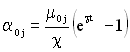

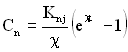Таким чином, загальні витрати на ТЗ можна визначити за формулою:

.

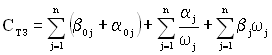Далі розділимо задане значення параметрів відмов між елементами ТЗ.

При послідовному з'єднанні елементів задані значення параметра потоку ТЗ ω_і і елементів ω_j пов'язані співвідношенням:

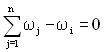.                     (3.15)

Використовуючи вираз (3.15) можна знайти такі значення ω_j, при яких загальні витрати на ТЗ будуть мінімальними.

Для цього скористаємося методом невизначених множників Лагранжа. Згідно з цим методом складають функцію:

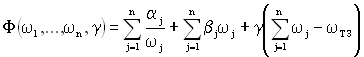, (3.16)

де γ – невизначений множник.

Далі прирівняємо до нуля частинні похідні від функції (3.16) по ω₁,…, ω_n в результаті чого отримаємо:

.

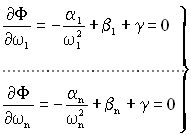З цих рівнянь визначимо невизначений множник γ, який дорівнює:

.

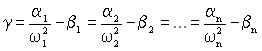Звідки отримаємо:

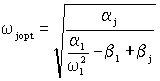. (3.17)

Підставивши вираз (3.17) в (3.15), отримаємо:

.

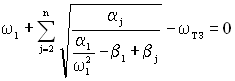Це рівняння легше розв’язати графічно, переписавши у вигляді:

,

де

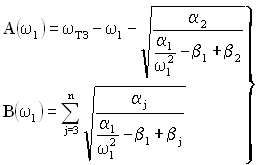. (3.18)

Для графічного розв’язання рівняння (3.18) обчислюються і заносяться на графік значення A(ω₁) і B(ω₁).

Абсциса точки перетину кривих визначає шукане значення ω_1оpt (рис. 3.6).

Надалі, використовуючи формулу (3.17), послідовно визначимо всі значення ω_jоpt.

Для спрощення обчислень можна переписати формулу (3.17) у вигляді

,

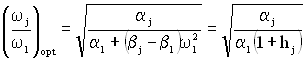де .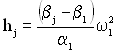

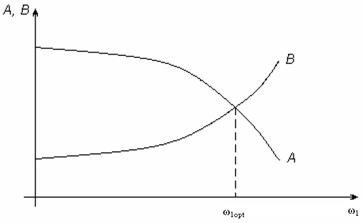
Рисунок 3.6 – Характеристики зміни параметрів A(ω₁) і B(ω₁)

Для полегшення обчислень може бути побудована номограма (рис. 3.7).

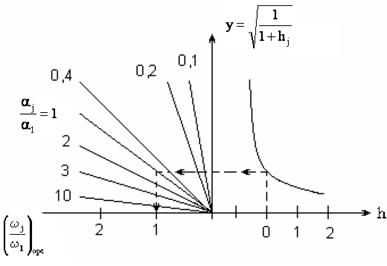
Рисунок 3.7 – Номограма для визначення оптимальних значень відношення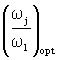

У правому квадранті розраховують значення 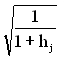, в лівому квадранті здійснюється множення на . Хід обчислень показаний стрілками (рис. 3.7).

Вирази для A(ω₁) і B(ω₁) можна записати так:

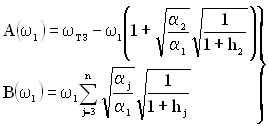. (3.19)

По черзі задаючи значення ω₁, можна знаходити за номограмою значення добутку коренів і використовувати їх у формулі (3.19).

Для даного прикладу:

(год)^-1;

;

;

;

;

.

Використовуючи (3.19) будуємо на одних осях графіки A(ω₁) і B(ω₁).

Перетин дає ω_1оpt = 1,43·10^-6 (год)^-1.

Визначені за допомогою номограм інші значення параметра потоку відмов складають: ω_2оpt = ω_3оpt = ω_4оpt = 2,86·10^-6 (год)^-1.