4.4 Метод оцінки надійності за графом можливих станів ТЗ

Цей метод заснований на методі диференційних рівнянь, при якому доводиться розв’язувати систему лінійних алгебраїчних рівнянь. Структура визначників цієї системи дозволяє сформулювати правило перебування виразів для ПН безпосередньо за графом.

Таке правило для виразів стаціонарної ймовірності перебування ТЗ в j-му стані полягає в такому: проходять найкоротші шляхи (без повернення) із усіх крайніх станів у кожен стан ТЗ за напрямком стрілок і перемножують усі інтенсивності переходів.

Кожна інтенсивність переходу враховується тільки один раз. Ймовірність перебування в j-му стані для графів без кілець визначається за формулою

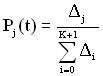, (4.17)

де – добуток інтенсивностей переходів із усіх найкоротших станів відповідно в j-ті та i-ті при русі за найкоротшим шляхом в напрямку стрілок;

(K+1) – кількість станів ТЗ.

Найкоротшими вважаються стани, що не мають вихідних стрілок при невідновлюваному ТЗ і мають не більше однієї вихідної стрілки при відновлюваному ТЗ.

Застосовуючи це правило можна отримати формулу для (коефіцієнта готовності ТЗ) без складання і розв’язання диференційних рівнянь.

Приклад 4.2

ТЗ складається з трьох вузлів. Відмова будь-якого вузла – відмова ТЗ. Відомі інтенсивності відмов та інтенсивності відновлень вузлів ТЗ. Визначіть – коефіцієнт готовності ТЗ.

Розв’язування:

Зобразимо граф ТЗ відповідно до умови задачі (рис. 4.2). Використовуючи викладене вище правило, визначаємо за графом (рис. 4.2) коефіцієнт готовності ТЗ

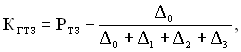(4.17, а)

де ; ; ; .

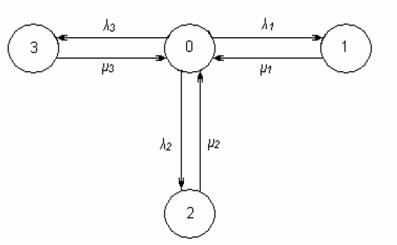
Рисунок 4.2 – Граф станів ТЗ, що заданий за умовою задачі

Підставляючи та (4.17, а) остаточно отримаємо

.

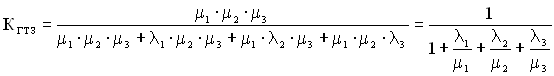Для нестаціонарного стану знаходять вираз для перетворення Лапласа ймовірності перебування в розглянутому стані.

4.5 Розрахунок втрат продуктивності ТЗ через ненадійність елементів

Як правило в таких випадках знаходять середні втрати за одиницю часу як математичне сподівання втрат вихідного ефекту за одиницю часу

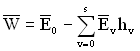, (4.18)

де – середній вихідний ефект за одиницю часу для цілком роботоздатного абсолютно надійного (ідеального) ТЗ;

– ймовірність перебування ТЗ в V-му стані (або доля часу перебування ТЗ в V-му стані);

– кількість можливих станів ТЗ.

Іноді зручніше обчислювати відносні середні втрати через ненадійності

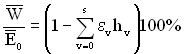, (4.19)

де 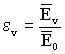– коефіцієнт зниження ефекту у V-му стані.

Основні труднощі виникають при визначенні ймовірностей перебування ТЗ в різних станах. Тому в результаті попереднього аналізу необхідно сформулювати деяке правило (припущення) і дотримуватись його в ході розрахунку.

Найбільш доцільними є такі з припущень:

1. Можливий (n+1) стан ТЗ. Один стан відповідає роботоздатності всіх елементів. Інші стани відповідають нероботоздатності одного з n елементів.

Вихідний ефект відповідає тільки одному стану при роботоздатності всіх елементів: «схема одного стану»;

2. Схема аналогічна попередній, але при відмові одного елемента виникає V-ий стан, якому відповідає вихідний ефект : «схема одної відмови»;

3. Можливі лише такі стани ТЗ, при яких не більше двох його елементів нероботоздатні: «схема двох відмов». Загальна кількість станів .

Доля часу перебування ТЗ в іншому, крім зазначених вище, стані вважається дуже малою.

Розрахунки втрат продуктивності ТЗ через ненадійність елементів доцільно проводити, переходячи послідовно від схеми одного стану до схем одного, двох і т. д. відмов елементів.

При «схемі одного стану» коефіцієнт ефективності для цього стану , для інших станів . При цьому відносні середні втрати обчислюються за формулою

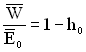, (4.20)

де – ймовірність того, що всі елементи роботоздатні.

Ймовірність обчислюється за значеннями коефіцієнтів готовності всіх j-х елементів або за формулою (4.13)

.

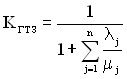При схемі «одної відмови» обчислюються ймовірності перебування ТЗ в кожному V-му із (n+1) станів за формулою

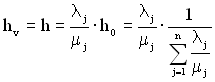. (4.21)

При цьому

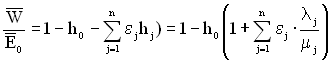. (4.22)

Збільшення відносної продуктивності ТЗ при розрахунку за схемою одної відмови може бути грубо оцінено за формулою

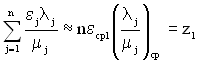, (4.23)

де – орієнтовна оцінка середнього коефіцієнта ефекту для стану ТЗ, у якому не працює один елемент (інші (n-1) працюють);

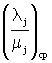– середнє значення відношення для елементів ТЗ.

Для ТЗ з різними та обчислення значно ускладнюються.

При розрахунку за «схемою двох відмов» обчислення значно ускладнюються через різке збільшення кількості розглянутих станів. Тому часто доводиться застосовувати ЕОМ. Послідовність обчислення така ж: за графом обчислюють середні втрати за формулою (4.19).

Щоб вирішити питання про доцільність розрахунку за «схемою двох відмов» перепишемо формулу (4.19) у вигляді

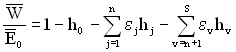, (4.24)

де .

У виразі (4.24) перша сума характеризує продуктивність ТЗ при одній відмові, а друга – при двох відмовах.

Питання для самоконтролю

1. Для яких законів розподілу часу безвідмовної роботи використовуються методи інтегральних та диференційних рівнянь при розрахунку надійності ТЗ?

2. Проаналізуйте переваги і недоліки методу диференційних рівнянь та методу розрахунку надійності за графом можливих станів ТЗ.

3. Покажіть (доведіть), чому при використанні методу оцінки надійності за графом можливих станів ТЗ немає необхідності у складанні та розв’язанні системи алгебраїчних рівнянь.

4. Які методи набули найбільшого поширення для опису надійності технічних засобів?

5. Проведіть порівняльний аналіз переваг і недоліків усіх трьох розглянутих методів розрахунку надійності.

6. Наведіть вираз для розрахунку відносних середніх втрат.

7. Наведіть вираз для визначення ймовірності перебування в j-му стані для графів без кілець.

8. Наведіть приклад графу станів ТЗ та поясніть як за цим графом складається система диференційних рівнянь.

9. Чому буде дорівнювати ймовірність перебування ТЗ в j-му стані при використанні методу диференційних рівнянь?

10. За яким виразом розраховується коефіцієнт готовності ТЗ в методі диференційних рівнянь?

11. Наведіть вираз для розрахунку функції готовності ТЗ в методі диференційних рівнянь та як записується при цьому нормована умова.

12. Чому дорівнює ймовірність появи відмови основного елемента протягом малого інтервалу часу при використанні методу інтегральних рівнянь?

13. Наведіть вираз для розрахунку ймовірності дубльованого ТЗ з холодним резервом.

14. Наведіть вираз для розрахунку щільності напрацювання ТЗ до відмови .

15. Якщо ТЗ має один основний і (K–1) резервний елемент, то за якою рекурентною формулою розраховується ймовірність безвідмовної роботи?