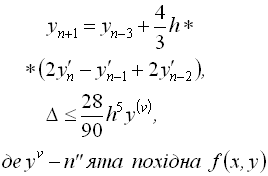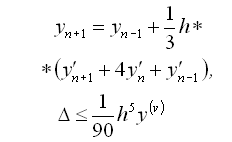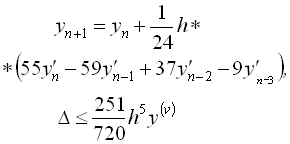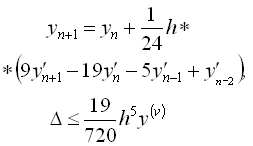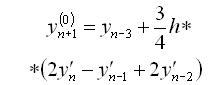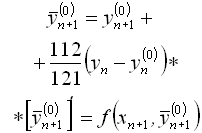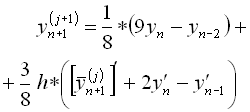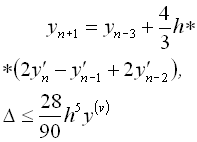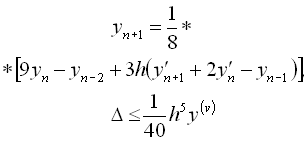4.1.2 Багатокрокові методи

 

В цих методах для обчислення значення нової точки використовується інформація про декілька значень, що отримані раніше. Для цього використовуються дві формули: прогнозу і корекції. Алгоритм обчислення для всіх методів прогнозу і корекції однаковий та зображений на рисунку4.3. Вказані методи відрізняються лише формулами і не мають властивості “самостартування”, оскільки вимагають знання попередніх значень. Перш ніж використовувати метод прогнозу і корекції, обчислюють початкові дані за допомогою будь-якого однокрокового методу. Часто для цього використовують метод Рунге – Кутта.

Обчислення виконують таким чином. Спочатку за формулою прогнозу та початковим значенням змінних знаходять значення . Індекс (0) означає, що значення, яке прогнозується, є одним із послідовності значень по мірі їх уточнення. За значенням за допомогою початкового диференціального рівняння (4.1.) знаходять похідну , яка після цього підставляється у формулу корекції для обчислення уточненого значення . В свою чергу, за знаходять похідну . Якщо це значення не достатньо близьке до попереднього, то воно вводиться у формулу корекції і ітераційний процес продовжується. У випадку близькості значень похідних визначається , яке і є остаточним. Після цього процес повторюється на наступному кроці, на якому обчислюється .

Зазвичай при виведенні формул прогнозу і корекції розв’язок рівняння розглядають як процес наближеного інтегрування, а самі формули отримують за допомогою методів чисельного інтегрування.

Якщо диференціальне рівняння проінтегрувати в інтервалі значень від x_n до x_n+k , то результат матиме вигляд

.

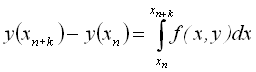Цей інтеграл не можна обчислити безпосередньо, тому що y(x) – невідома функція. Вибір методу наближеного інтегрування і буде визначати метод розв’язання диференціальних рівнянь. На етапі прогнозу можна використовувати будь-яку формулу чисельного інтегрування, якщо до неї не входить попереднє значення .

В таблицю 4.1 зведені найбільш розповсюджені формули прогнозу і корекції. Для більшості методів прогнозу і корекції оцінюють похибку, користуючись таким співвідношенням:

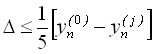
Мірою похибки слугує і є , що входить до алгоритму рисунку 4.3.

Часто в довідниках приводяться більш точні формули для оцінки похибки багатокрокових методів.

При виборі величини кроку можна скористатися умовою:

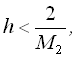
де .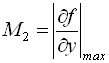

Виконання цієї умови необхідно для збіжності ітераційного процесу відшукання розв’язку.

Однак у багатьох практичних випадках складність оцінки величини приводить до того, що найбільш зручним для вибору кроку є спосіб, побудований на оцінці D у процесі обчислень і зменшенні кроку, якщо похибка надто велика. При цьому необхідно враховувати, що оптимальне число ітерацій дорівнює двом.

               Таблиця 4.1 Найбільш розповсюджені формули прогнозу і корекції.

Метод	Формула прогнозу	Формула корекції
Мілна
Адамса – Башфорта
Хеммінга	Уточнення прогнозу

Основні особливості, що притаманні багатокроковим методам:

1) за допомогою цих методів не можна розпочати розв’язання задачі, оскільки для їх використання необхідна інформація про значення функції в кількох точках;

2) можна отримати оцінку похибки зрізання, не звертаючись до обчислення додаткових величин;

3) методи прогнозу і корекції не дозволяють легко змінювати крок обчислень, для цього необхідно весь ітераційний процес починати спочатку.

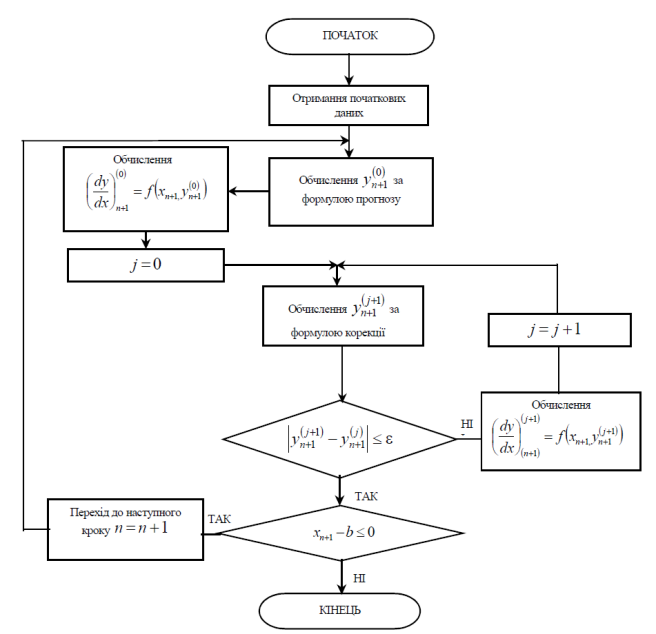
Рисунок 4.4 – Алгоритм методів прогнозу та корекції