5.2 Розв’язання різних типів диференціальних рівнянь в частинних похідних
Практичні методи і алгоритми розв’язання різних виглядів диференціальних рівнянь в частинних похідних мають свої особливості і вимагають окремого розгляду на прикладі найбільш розповсюджених задач.
5.2.1 Еліптичні рівняння
До еліптичних рівнянь (elliptic equations) приводиться багато різних фізичних задач: розрахунок напружень, які виникають при пружному скруті довгого циліндричного стрижня; розподіл електричних напруг на площині, що проводить струм; задача про стаціонарні течії тепла в двовимірному тілі. Часто виникає необхідність розв’язання таких задач і в теорії автоматичного керування. Більшість еліптичних рівнянь описується рівнянням Пуассона або його окремим випадком - рівнянням Лапласа.
Розглянемо класичну задачу Діріхле для рівняння Лапласа в прямокутній області, яка формулюється таким чином: знайти неперервну функцію f(x,y), яка задовольняє 
всередині прямокутної області рівняння Лапласа:
і приймає на границі області задані значення:
x=0; f (0,y) = f1 (y),
x=a; f (a,y) = f2 (y),
y=0; f (x,0) = f3 (x),
y=b; f (x,b) = f4 (x).
Введемо в області розв’язання двовимірну сітку з кроком h по осі x і l по осі y. Тоді, користуючись прийнятими в попередніх розділах позначеннями і апроксимуючи рівняння Лапласа різницевим рівнянням, отримаємо таку систему лінійних рівнянь (приймемо для спрощення l=h):
(5.2)
при i=1,2,…,n-1; j=1,…,m-1.
Ця система рівнянь має велику кількість нульових елементів і задовольняє умові збіжності при використанні ітераційних методів. Найбільше використання для розв’язання таких систем знайшов метод Гаусса - Зейделя, який, коли застосовується до еліптичних різницевих рівнянь, називається методом Лібмана або методом послідовних зміщень. Порядок ітерацій можна простежити, переписавши систему ( 5.2. ) у вигляді:
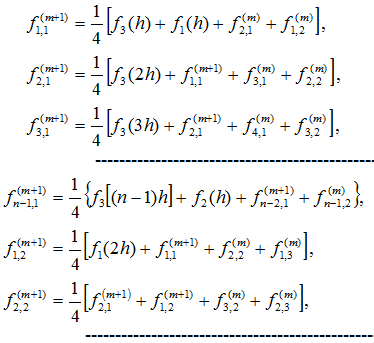
де верхніми індексами позначено порядковий номер ітерації: m - попередня, m+1 - наступна.
Зазвичай вважають 
для всіх i, j. Система рівнянь легко розв’язується на ЕОМ. Взагалі кажучи, будь-які еліптичні рівняння, які не містять
, зводяться до систем різницевих рівнянь, які можна розв’язувати як методом Лібмана, так і іншими ітераційними методами (Якобі, послідовної верхньої релаксації та ін.), оскільки для них виконуються умови збіжності. Для еліптичних рівнянь, які містять в загальному вигляді, питання про збіжність ітераційних методів не має теоретичного розв’язку і необхідно розглядати отриману систему рівнянь в кожному конкретному випадку.
5.2.2 Гіперболічні рівняння
Найчастіше зустрічається в інженерній практиці гіперболічне рівняння в частинних похідних (hyperbolic equations in partial derivatives) – хвильове рівняння, яке описує різні види коливань: коливання струни або мембрани, розповсюдження звукових хвиль в різних середовищах тощо.
В загальному вигляді задача формулюється таким чином: знайти функцію f (x, t), яка задовольняє всередині області 
={(x, t) , 0
x a, 0 t T } рівняння
Початкові
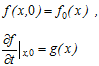
і граничні умови
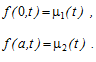
Оскільки заміна змінних t =c t приводить рівняння до вигляду:
то надалі приймаємо с=1.
Переходячи до різницевого рівняння на сітці з кроком h по x й 
по t з центральними різницями, отримаємо
.
Якщо ввести 
, то вираз для 
прийме вигляд:
. (5.3)
Схема розв’язання за рівнянням (5.3) називається тришаровою, оскільки так зв’язує значення 
на трьох часових шарах j-1, j, j+1. Ця схема явна й дозволяє в явному вигляді виразити 
через значення f з попередніх шарів (існують неявні схеми, основані на використанні інших обчислювальних шаблонів, але вони вимагають більшого обсягу обчислень при розв’язанні системи рівнянь). Для знаходження розв’язку на першому шарі зазвичай використовують інтерполяційні методи. Наприклад,
. (5.4)
Співвідношення сторін сітки визначається величиною r, яка є мірою стійкості отриманого розв’язку. При r>1 розв’язок нестійкий, при r<1 хоча й стійкий, але точність його при зменшенні r спадає, при r=1 різницевий розв’язок стійкий і збігається з точним. Вибір r=1 зручний ще й тим, що при цьому спрощується співвідношення (5.4)
5.2.3 Параболічні рівняння
Прикладом задачі, яка приводить до параболічного рівняння (parabolic equation) в частинних похідних, є задача про теплопередачу по довгому стрижню. Вона описується рівнянням теплопередачі (або дифузії).
Задача полягає у знаходженні f (x, t), яка задовольняє в області ={(x, t) 0 x a, 0 t T } рівняння
Початкові
f (x, 0)=f0 (x)
і граничні умови першого роду
Заміна змінних t = k t приводить рівняння до вигляду
тому надалі будемо вважати k=1.
Можливі два варіанти отримання різницевого рівняння на сітці з кроком h по x та по t (рисунок 5.4).
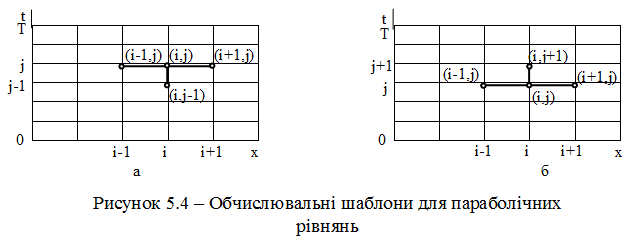
Варіант з апроксимацією на чотириточковому шаблоні (рисунок 5.4, а) приводить до неявної двошарової різницевої схеми
де 
Ця схема доповнена рівняннями, отриманими з крайових умов
зводить задачу до розв’язання до системи рівнянь, які мають стійкий розв’язок при будь-яких значеннях r.
Варіант з апроксимацією на чотириточковому шаблоні (рисунок 5.5, б) призводить до явної двошарової системи
Ця схема стійка тільки при r0,5, що приводить до необхідності проводити обчислення з дуже малим кроком по t, який обмежує швидкодію і вимагає більших витрат часу ЕОМ. Тому для параболічних рівнянь більш широке розповсюдження отримала неявна схема.
5.3 Загальні рекомендації до розв’язання диференціальних рівнянь в частинних похідних
На початковому етапі вибирається метод розв’язання задачі. Зазвичай простіше використовувати різницевий метод, який вимагає більш простої підготовки задачі до розв’язання, але в ряді випадків для задач з добре розробленою теорією (наприклад, задач механіки) доцільно звертатися до методу cкінченних елементів.
При визначенні кроку розв’язання задачі основним фактором є точність (якщо висока, то необхідна або дуже дрібна сітка, або розбиття на дуже малі елементи). При цьому необхідно враховувати, що похибка різницевих методів має другий порядок. Її оцінку можна проводити аналогічно звичайним диференціальним рівнянням за методом Рунге.
У випадку симетрії в області розв’язання можна число вузлів зменшити в два або навіть у чотири рази (при симетрії по обох осях координат). Це дозволяє отримати економію часу та обсягу обчислень.
Велику роль для ефективного розв’язання задачі грає вибір початкових наближень. При використанні ітераційних методів від цього значною мірою залежить швидкість збігання. Часто має сенс розв’язувати задачу в декілька етапів: на першому за допомогою грубої сітки (або розбиття на крупні елементи) отримують добре початкове наближення, на наступних - шукають більш точний розв’язок на дрібній сітці.
Контрольні запитання та завдання
1. Наведіть приклади інженерних задач, які описуються диференціальними рівняннями в частинних похідних.
2. На які види можна поділити диференціальні рівняння другого порядку в частинних похідних в залежності від коефіцієнтів, які входять до них?
3. Які методи існують для розв’язання диференціальних рівнянь в частинних похідних?
4. Як конструюються обчислювальні шаблони для частинних похідних? Отримайте обчислювальні шаблони для оператора Лапласа та бігармонічного оператора.
5. Як використовується різницевий метод у випадку, коли границя області, де шукають розв’язок, не проходить через вузли сітки? Наведіть приклад обчислювального шаблону?
6. Якими різницевими методами розв’язується класична задача Діріхле для рівнянь Лапласа в прямокутній області? Доведіть їх збіжність.
7. Отримайте тришарову схему розв’язання гіперболічних рівнянь. В яких випадках розв’язок стійкий?
8. Порівняйте ефективність використання явної і неявної схем розв’язання параболічних рівнянь в частинних похідних.
9. Як вибирається крок при розв’язанні диференціальних рівнянь в частинних похідних?
