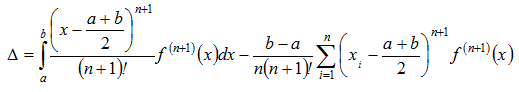6.4.2 Формули Ньютона - Котеса

 

Для виведення формул Ньютона - Котеса інтеграл зображується у вигляді

(6.21)

де – вузли інтерполяції; – коефіцієнти, які залежать від вигляду формули; – похибка квадратурної формули.

     Замінюючи в (6.21) підінтегральну функцію відповідним інтерполяційним поліномом Лагранжа для рівновіддалених вузлів з кроком , можна одержати наступну формулу для розрахунку коефіцієнтів при довільній кількості вузлів.

(6.22)

де – приведена змінна.

     Звичайно коефіцієнти називають коефіцієнтами Котеса.

     При цьому формула (6.21) приймає вигляд

     (6.23)

і має такі властивості:

При із (6.22) та (6.23) отримаємо формули трапецій і Сімпсона:

 

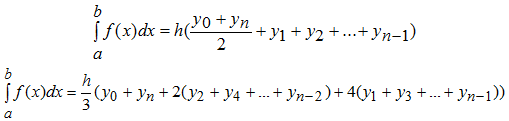
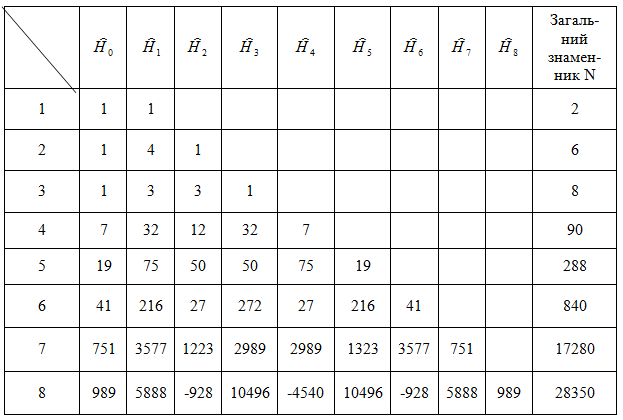
В таблиці 6.7 наведені значення коефіцієнтів для      Похибки формул трапецій і Сімпсона визначаються, відповідно, із виразів

де максимальні значення другої та четвертої похідної

     Таблиця 6.7 Коефіцієнти Котеса

Складові формули Ньютона – Котеса отримаємо шляхом комбінації простих формул. Наприклад, для формул трапецій і Сімпсона (для парних n):

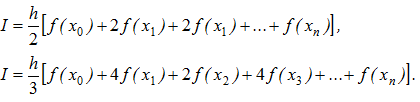
     Причому похибки складових формул будуть відповідно

     Аналогічно можна отримати складові формули Ньютона – Котеса більш високих порядків.

     Для оцінки похибки на практиці можна користуватись методом Рунге (екстраполяції Річардсона), аналогічно тому,як це робиться для одно- крокових методів розв’язання задачі Коши.

 

          6.4.3 Формула Чебишева

Формула (6.6) може бути приведена до вигляду

     (6.24)

заміною змінних

.

При виведенні формули Чебишева використовуються такі умови:

  •  коефіцієнти рівні між собою;
  •  квадратурна формула (6.24) точна для всіх поліномів до степеня включно.

    При цих умовах формула (6.24) має вигляд:

    (6.25)

         Для знаходження використовуємо другу умову, згідно з якою формула (6.25) повинна бути точною для функції вигляду

    Після підстановки цих функцій в (6.25) отримаємо систему рівнянь

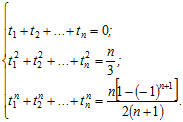              (6.26)

         Система рівнянь (6.26) має розв’язок при В цій обмеженій точності і полягає недолік формули Чебишева. Значення для різних наведені в таблиці 6.8.

        

    Таблиця 6.8

    Значення абсцис в формулі Чебишева

    		 

    2

    1;2

    0,577350

    		  

    6

    1;6

    0,866247

    3

    1;3

    0,707107

    		  

    2;5

    0,422519

    2

    0

    		  

    3;4

    0,266635

    4

    1;4

    0,794654

    		  

    7

    1;7

    0,883862

    2;3

    0,187592

    		  

    2;6

    0,529657

    5

    1;5

    0,832498

    		  

    3;5

    0,323912

    2;4

    0,374513

    		  

    4

    0

    3

    0

    		        

    Для довільного інтервалу (a, b) формула (6.25) приймає вигляд

    де .

         Похибка обчислень за методом Чебишева:

     

    •