4.1.1 Однокрокові методи
Найбільш простим однокроковим методом, який потребує мінімальних затрат обчислювальних ресурсів, але дає змогу обчислювати результат із порівняно низькою точністю, є метод Ейлера.
В цьому методі для оцінки наступної точки на кривій y=f(x) використовується лише один лінійний член в формулі Тейлора,
де yў (x0) визначається з початкового рівняння.
Цей процес можна розповсюдити на наступні кроки:
.
Метод Ейлера є методом першого порядку 
,
де 
, M0 , M1, M2 - визначаються як
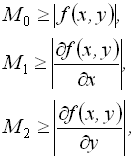
для всіх 
i 
.
Метод Ейлера, крім значної похибки зрізання часто буває нестійким (малі локальні помилки призводять до значного збільшення глобальної).
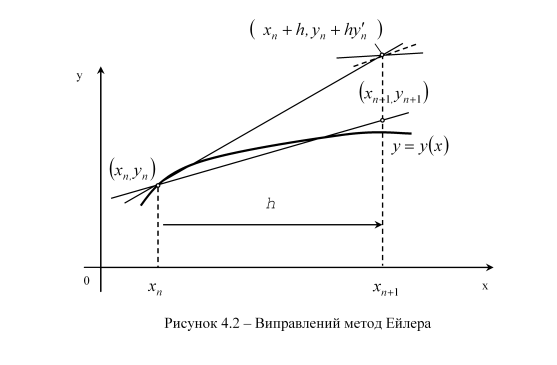
Цей метод можна вдосконалити різними способами. Найбільш відомі два з них: виправлений метод Ейлера і модифікований метод Ейлера (в літературі зустрічаються інші назви цих методів, наприклад, модифікований метод Ейлера й удосконалений метод ламаних).
Ітераційні формули для цих методів мають вигляд, відповідно:
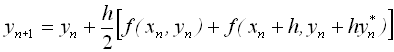
і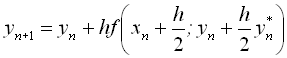 
,
де 
Геометрична інтерпретація зображена на рисунках 4.2., 4.3.
Це методи другого порядку, їх похибка має третій степінь, що досягається покращенням апроксимації похідної. Ідея полягає у спробі зберегти або оцінити член другого порядку у формулі Тейлора. Однак збільшення точності вимагає додаткових витрат машинного часу на обчислення 
. Ще більш висока точність може бути досягнута при обчисленні вищих похідних і збереженні більшої кількості членів ряду Тейлора. Такими методами є методи Рунге – Кутта.
Принцип, на якому побудований модифікований метод Ейлера, можна пояснити, користуючись рядом Тейлора і зберігаючи в ньому член з 
. Апроксимація другої похідної 
здійснюється кінцевою різницею
.
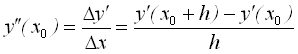Аналогічно обчисленню другої похідної в кінцево – різницевому вигляді можна обчислити більш високі похідні: значення n-ї за значеннями попередньої (n-1)-ї.
Метод Рунге – Кутта дає набір формул для обчислення координат внутрішніх точок, які потрібні для реалізації цієї ідеї. Оскільки існує ряд способів знаходження цих точок, то метод Рунге –Кутта об’єднує цілий клас методів для розв’язання диференціальних рівнянь першого порядку.
Найбільш розповсюджений класичний метод четвертого порядку точності:
,
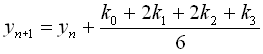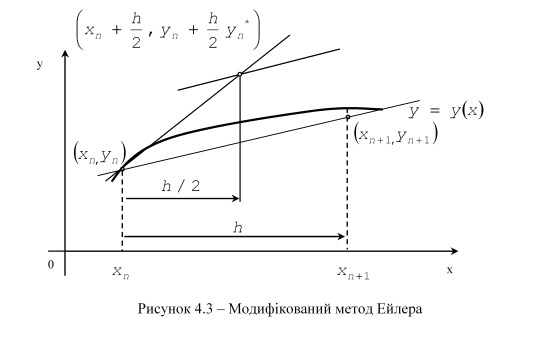де
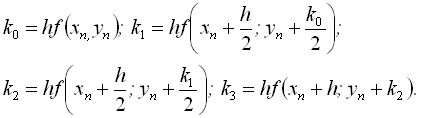
Метод Ейлера і його модифікації ще називають методами Рунге – Кутта першого і другого порядку. Метод Рунге – Кутта має значно більш високу точність, що дозволяє збільшити крок розв’язання. Його максимальну величину визначає припустима похибка. Такий вибір часто здійснюється автоматично і включається як складова частина в алгоритм, побудований за методом Рунга – Кутта.
Будь-яку з формул однокрокових методів можна використовувати для розв’язання систем диференціальних рівнянь і диференціальних рівнянь вищих порядків.
Для опису складних динамічних процесів використовують системи диференціальних рівнянь. Найбільше розповсюдження отримали системи диференціальних рівнянь першого порядку:
.
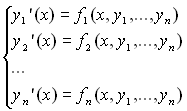Для однозначного розв’язку цієї системи задають початкові умови:
.
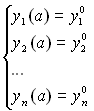Ця система рівнянь з наведеними початковими умовами називається задачею Коші для системи n диференціальних рівнянь першого порядку. У векторному вигляді вона записується так:
.
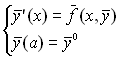У формулах однокрокових методів для розв’язку такої задачі Коші потрібно лише перейти до векторної форми. Наприклад, формули метода Рунге-Кутта 4-го порядку розв’язку задачі Коші для системи n диференціальних рівнянь першого порядку мають вигляд:
,
де
,
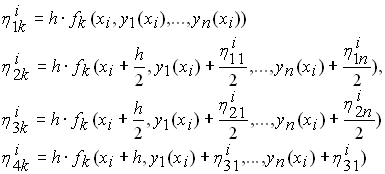– номер рівняння,
– номер вузла, 
.
Задачу Коші для диференціального рівняння порядку n можна звести до задачі Коші для системи n диференціальних рівнянь першого порядку.
Нехай задача Коші має вигляд:
.
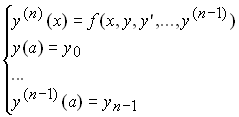Зробимо заміну:
.
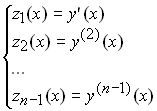Як результат, отримаємо систему диференціальних рівнянь першого порядку:
.
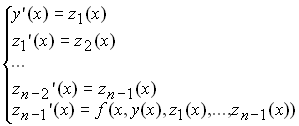Початкові умови приймуть вигляд:
.
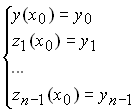Як приклад розглянемо розв’язання звичайного диференціального рівняння другого порядку:
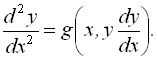
Нехай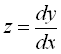 
, тоді 
;
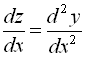і система набуває вигляду
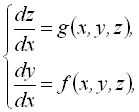
де 
.
Задача Коші в цьому випадку містить дві початкових умови:
; 
Формули Рунге – Кутта для цього випадку мають вигляд:
і 
,
де 
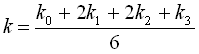, а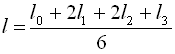 
.
де
, 
,
,
, 
.
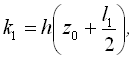
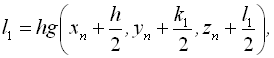
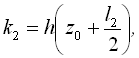
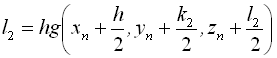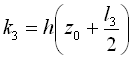Раніше було відзначено, що помилка зрізання при використанні методу Рунге – Кутта n-го порядку 
. Обчислення верхніх границь для коефіцієнта с являє собою складну задачу, пов’язану з необхідністю оцінки ряду додаткових параметрів. Існує декілька способів для оперативного обчислення с. Найбільшого поширення набув екстраполяційний метод Річардсона (ще його називають методом Рунге), коли послідовно знаходять значення yn з кроком h і з кроком 
, а після цього прирівнюють отримані величини та визначають с з рівняння:
,
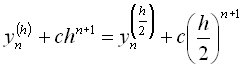що відповідає точному значенню yn.
Отримаємо оціночне співвідношення:
.
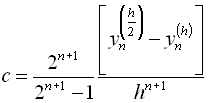Можна виділити загальні риси однокрокових методів:
1. Щоб отримати інформацію у новій точці, потрібно мати дані лише в одній попередній точці. Цю властивість називають “самостартуванням”.
2. В основі всіх однокрокових методів лежить розкладання функції в ряд Тейлора, в якому зберігаються члени, що містять степені до k включно. Ціле число k називається порядком методу. Похибка на кроці має порядок k+1.
3. Всі однокрокові методи не вимагають обчислення похідних – обчислюється лише сама функція, але можуть вимагатися її значення в декількох проміжних точках.
Властивість “самостартування” дозволяє легко змінювати розмір кроку обчислення.
