2.3 Структура ідеальних кристалів

Розглянемо детальніше внутрішню структуру кристалів. Для її опису зручно скористатися поняттям кристалічних граток (crystal grating). Розрізняють прості гратки (гратка Браве) і гратку з базисом.

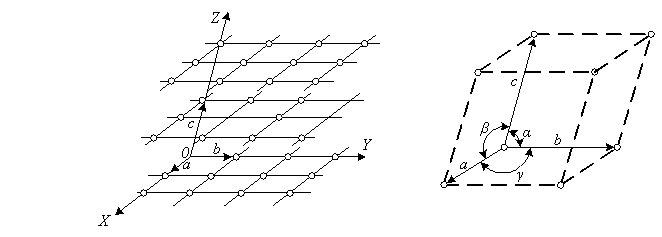
Прості гратки. З геометричної точки зору правильне розміщення частинок в кристалі, що періодично повторюється, можна описати за допомогою операції паралельного переміщення або трансляції. На рис, 2.6, а показані гратки, одержані трансляцією частинки 0 уздовж трьох осей: осі х на відрізки а, 2а, ..., осі у на відрізки , 2, .., осі на відрізки с, 2с, ... Вектори а, , с називаються елементарною коміркою (simply cell) кристала (рис. 2.6, б). Всі елементарні комірки кристала мають однакові форму і об'єм; у всіх вершинах комірок розташовуються однакові атоми. Тому всі вершини комірок еквівалентні один одному. Їх називають вузлами гратки.

Для характеристики елементарної комірки необхідно задати в загальному випадку 6 величин: три ребра комірки а, b, с і три кути між ними а, b, g. Ці величини називаються параметрами комірки. Часто за одиницю вимірювання довжини в гратках приймаються відрізки а, b, с; їх називають осьовими одиницями (axial unit). Елементарні комірки, що містять частинки тільки у вершинах, називаються простими або примітивними. На кожну таку комірку приходиться один атом. У ряді випадків для досягнення повнішого виразу симетрії граток елементарні комірки будують таким чином, що вони містять частинки не тільки у вершинах, але і в інших місцях. Найпоширенішими з них є об'ємоцентрична (ОЦ), гранецентрична (ГЦ) і базоцентрична (БЦ) комірка (див. рис. 2.7).

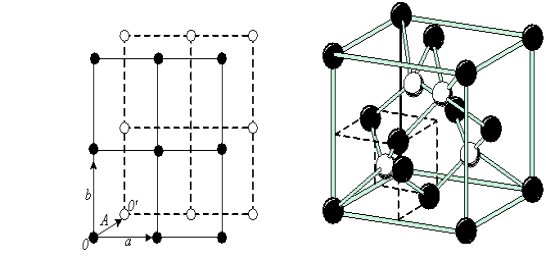
Гратки з базисом. Не всякі гратки можна одержати трансляцією одного атома. Як приклад на рис. 2.8, а показані двовимірні грати загального типу. Легко побачити, що при побудові таких граток за допомогою вектора трансляції її комірка не може бути вибрана одноатомною. Таку гратку можна подати у вигляді двох вставлених одна в одну граток Браве, кожна з яких визначається векторами трансляцій а і b. Зсув граток одна відносно одної описується додатковим вектором А, названим базисним (basis vector). Число таких векторів в загальному випадку може бути яким завгодно.

     а)                              б)

Рисунок 2.6 – Прості гратки (а) і елементарна комірка цих

граток (б)

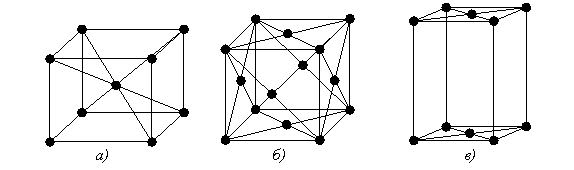
Рисунок 2.7 – Об’ємоцентрична (а), гранецентрична (б) і базоцентрична (в) комірки

Гратку загального типу називають граткою з базисом. Її можна побудувати за допомогою тих же трансляцій, що і кожну із складових гратки Браве, тільки транслювати треба не вузол, а базис, що задається сукупністю базисних векторів. Так, гратку, показану на рис. 2.8, а, можна одержати трансляцією базису, який складається з вузлів 0 і 0'.

а)                                   б)

Рисунок 2.8 – Гратки з базисом: а – плоска, б – об’ємна.

Як приклад тривимірних граток з базисом на рис. 2.8, б показані гратки алмазу. Базис таких граток містить два атоми з координатами 0, 0, 0 і 1/4, 1/4, 1/4. Кожний атом вуглецю оточений чотирма найближчими сусідами, розташованими у вершинах тетраедра, виділеного на рис. 2.8, б штриховими лініями.

Позначення вузлів, напрямів і площин в кристалі. Познайомимося стисло із загальноприйнятими позначеннями вузлів, напрямів і площин в гратках – з індексами Міллера.

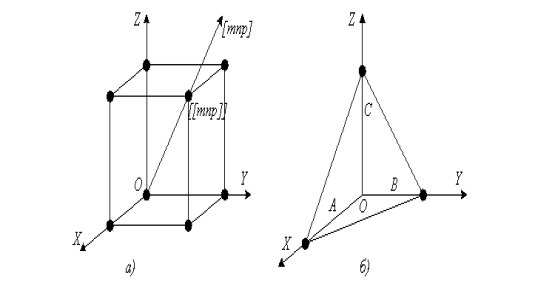
Рисунок 2.9 – Позначення вузлів і напрямів (а) і площин (б) в кристалі

Індекси вузлів (index knot). Положення будь-якого вузла гратки визначається заданням трьох координат (рис. 2.9, а): х, у, . Ці координати можна виразити так: x=ma, y=nb, z=pc, де a, b, c –параметри гратки; m, n, p – цілі числа. Якщо за одиниці вимірювання довжин прийняти параметри гратки, то координатами вузла будуть просто числа m, n, p. Ці числа називають індексами вузла і записують таким чином: [[mnp]].

Індекси напряму (index straight). Для опису напряму в кристалі вибирається пряма, що проходить через початок координат. Її напрям однозначно визначається індексами [[mnp]] першого вузла, через який вона проходить (рис.2.9,а). Тому індекси вузла одночасно є і індексами напряму. Індекси напряму позначаються так: [mnp].

Індекси площини (index flat). Ці індекси знаходяться таким чином: виражають відрізки А,В,С, які площина відсікає на осях гратки (рис.2.9,б), в осьових одиницях. Записують величини, обернені цим відрізкам 1/А, 1/В, 1/С.Одержані дроби зводять до спільного знаменника. Тоді числа , , приймаються за індекси площини і записуються так .