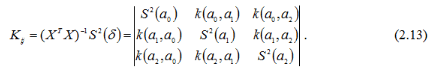Найбільш розповсюдженим методом для визначення оцінок параметрів регресійних моделей є метод найменших квадратів (МНК). В даному методі оцінки параметрів регресійної моделі визначають з умови, що сума квадратів відхилень експериментальних значень уі від розрахункових (теоретичних) значень мінімальна, тобто: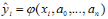

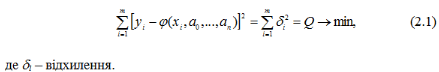
Види регресійної моделі:

При розгляді МНК обмежимося випадком, коли залежність задана поліномом, тобто:

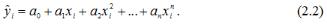
Відповідно до (2.1), найкращими значеннями коефіцієнтів a0, a1, an будуть ті, для яких сума квадратів відхилення:

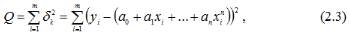
буде мінімальна. Мінімум функції багатьох змінних, як відомо, досягається тоді, коли всі її частинні похідні дорівнюють нулю. Тому, диференціюючи (2.3) за змінною аn, одержуємо:

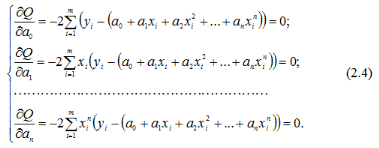
Після спрощення одержимо:

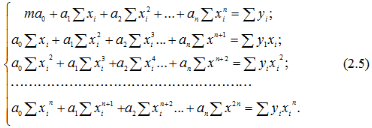
Розв’язок системи лінійних рівнянь знайдемо за допомогою визначників:

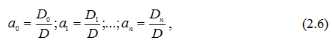де D – головний визначник системи (2.5),
Di – визначник, який отримується із головного визначника шляхом заміни стовпців коефіцієнтів при невідомих аі на стовпці з коефіцієнтами з вільними членами.
Виправлене середнє квадратичне коефіцієнтів аі виражається такою формулою:

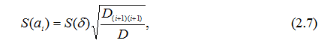
де D _(і+1)(і+1) – алгебраїчне доповнення елементів головного визначника D, отримане шляхом видалення з матриці визначника
стовпця (і+1) і рядка (і+1).

Стандартна похибка :

Надійний інтервал існування a _n обчислюється за формулою:

Виправлена дисперсія функції Y, визначається за формулою:

Параметри поліноміальної регресії, коли степінь полінома більше трьох, бажана визначати за допомогою матричного аналізу.

Наприклад: якщо визначаються параметри поліноміальної регресії 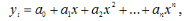, то коефіцієнти аі зручніше визначати за формулою:

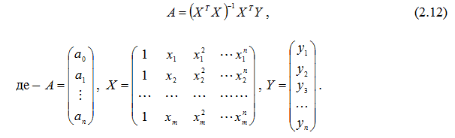
Визначити дисперсії параметрів рівняння регресії і кореляційних моментів можна за допомогою кореляційної матриці: