Методичні вказівки до проведення практичних занять та виконання контрольних робіт з дисципліни «Спецглави математики». Ч.2 для студентів напряму підготовки «Метрологія та інформаційно-вимірювальні технології» всіх форм навчання

2.6.2 Двофакторний дисперсійний аналіз


Математична модель двофакторного дисперсійного аналізу має вигляд:

У разі проведення дисперсійного аналізу досліджуваний масив даних, одержаних під час експерименту, поділяють на певні групи, які різняться дією на результати експерименту певних рівнів факторів.
Вважається, що досліджувана ознака має нормальний закон розподілу, а дисперсії в кожній окремій групі здобутих значень ознаки однакові. Ці припущення необхідно перевірити.
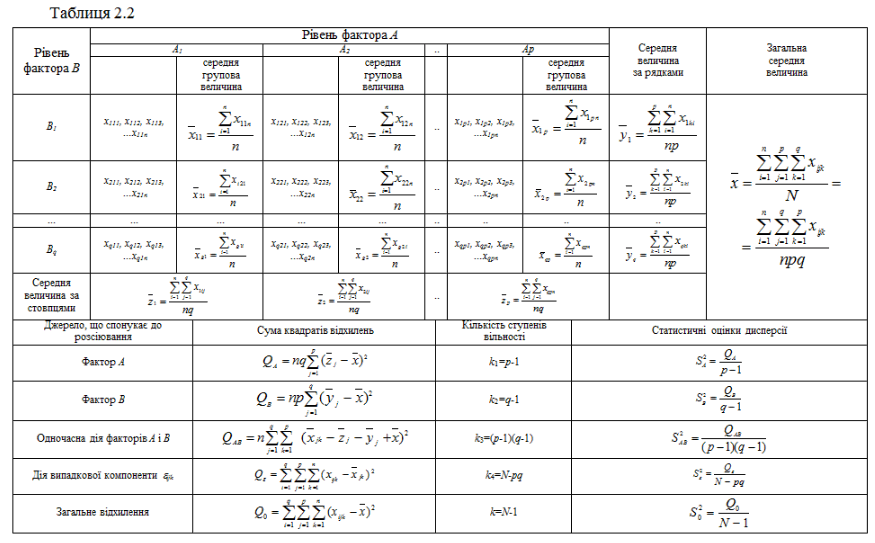
Для перевірки нульової гіпотези про відсутність впливу факторів або спільного впливу двох факторів на ознаку Х, результати експерименту зручно подати у вигляді таблиці, яка поділена на групи. Виходячи з даних таблиці, маємо, що:
середнє значення ознаки Х для кожної групи:
Середнє значення ознаки Х по стовпцях:
Середнє значення ознаки Х по рядках:
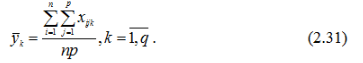
Загальне середнє ознаки Х:
Виправлена дисперсія, яка зумовлена впливом фактора А на ознаку Х:
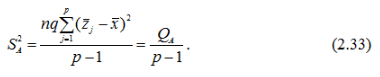
Виправлена дисперсія, яка зумовлена впливом фактора В на ознаку Х:
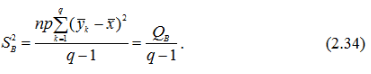
Виправлена дисперсія, яка зумовлена одночасним впливом на ознаку Х факторів А і В:
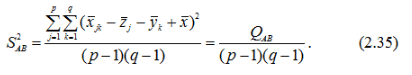
Виправлена дисперсія, яка зумовлена впливом на ознаку X випадкових факторів:
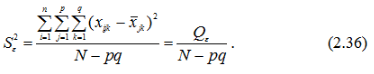
Виправлена загальна дисперсія дорівнює:
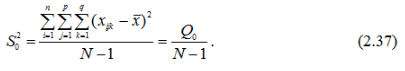
Для двофакторного дисперсійного аналізу повинно виконуватися рівняння:
Обчислюється розрахункове значення критерію Фішера:

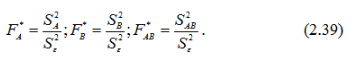
Контрольні питання