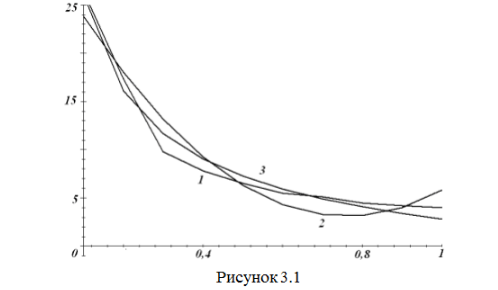
1. За даними результатів спостережень величин X i Y, які наведені у таблиці 3.1, визначити статистичні оцінки a ^* ₀, a ^* ₁, a ^* ₂ для параметрів a ₀, a ₁, a ₂ рівняння поліноміальної регресії y = a ₀ + a ₁х + a ₂х², надійний інтервал існування коефіцієнтів при надійній ймовірності р = 0,95, або іншій за вказівкою викладача, та оцінку дисперсії заданої функції. Обчислити кореляційне відношення R'.

2. За даними результатів спостережень величин X i Y, які наведені у таблиці 3.1, знайти статистичні оцінки 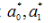для параметрів a ₀, a ₁ рівняння нелінійної регресії, виконавши перетворення функції y(x) до лінійної. Рівняння нелінійної регресії наведені в таблиці 3.2. Обчислити кореляційне відношення R'. За визначеними коефіцієнтами R', зробити висновок про міру щільності зв’язку вибраних рівнянь регресії.

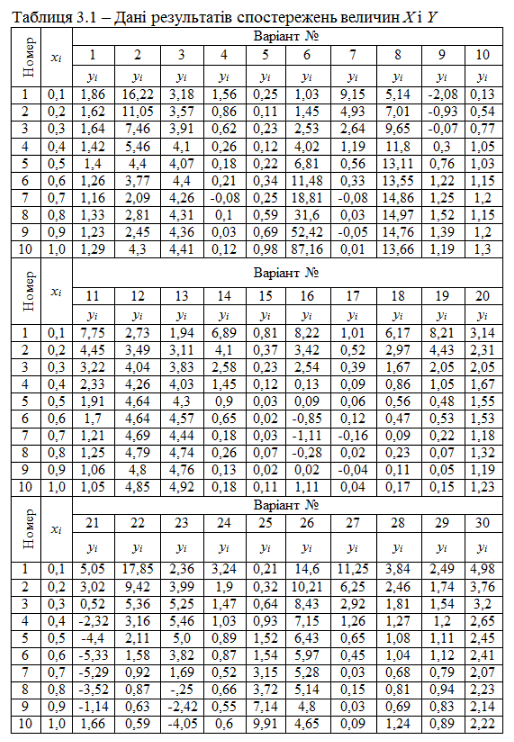
3. Побудувати в одній системі координат графіки: експериментальних точок, поліноміальної регресії та нелінійної регресії.

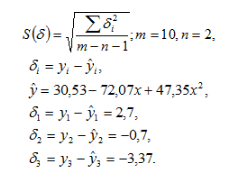
Як приклад, обчислення стандартної похибки наведені тільки для трьох точок, для інших точок розрахунки виконуються аналогічно.

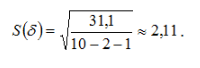
в) оцінка середньоквадратичного відхилення коефіцієнтів аn виражається формулою:

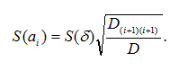
Оцінка середньоквадратичного відхилення коефіцієнта а ₀:

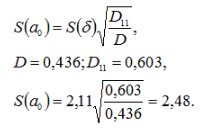
г) визначаємо надійний інтервал 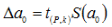для коефіцієнта а0, Коефіцієнт Стьюдента t _(P,k) знаходиться за спеціальною таблицею, якщо k = m-n-1 = 7, р = 0,95 коефіцієнт Стьюдента дорівнює 2,36.

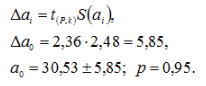
Аналогічно виконуються розрахунки коефіцієнтів а1, а2.
д) оцінку дисперсії функції y = a ₀ + a ₁х + a ₂х² визначаємо за формулою:

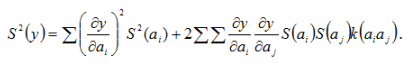
Оцінка кореляційного моменту розраховується за формулою:

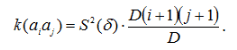
Визначимо оцінку кореляційного моменту між коефіцієнтами а ₀ і а ₁:

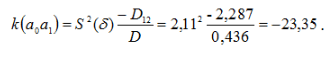
Аналогічно обчислюються оцінка кореляційних моментів k _(a0,a2) та k _(a1,a2).

Відповідні частинні похідні 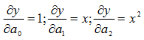, тоді:

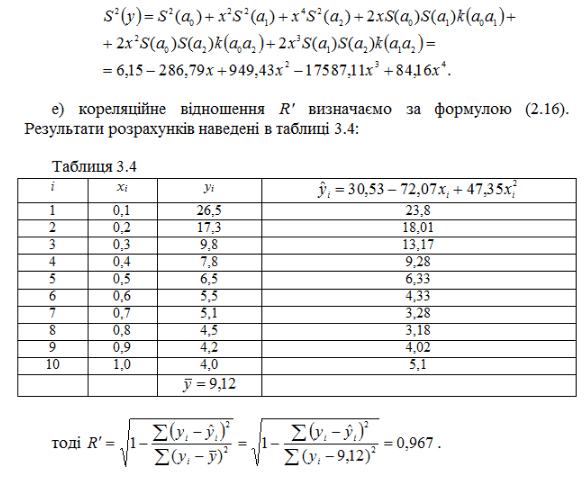
1.2 Визначимо всі необхідні параметри за допомогою матричного обчислювання,