3.4.2 Математичні моделі керування режимами в системі електропостачання шляхом підвищення ефективності технологічних БСК

Проведений аналіз умов роботи ЕПУ показав, що є деяка можливість для варіювання потужності БСК. Межі можливого варіювання обмежуються, з однієї сторони, вимогами технологічного процесу (відгалуження компенсаційного трансформатора T₂, яке забезпечує технологічний процес n-ої ЕПУ позначимо ζn) а з іншої – пропускною здатністю трансформаторів T₁ та T₂ або наявною потужністю БСК – (відповідне відгалуження для T₂ n-ої ЕПУ позначимо τn).

Для яких же цілей можна використати додаткову потужність конденсаторних батарей?

По-перше, для оптимального керування реактивною потужністю підприємства. Як згадувалось, печі графітації працюють з низьким коефіцієнтом потужності при великому споживанні реактивної потужності за абсолютною величиною. Далі цей випадок по тексту буде згадуватись як задача керування 1.

По-друге, враховуючи те, що ЕПУ є несиметричними електроприймачами і у вузлі навантаження має місце несиметрія напруг, то технологічні БСК однофазного виконання можна використати для симетрування напруг на збірних шинах 35 кВ з одночасною компенсацією реактивної потужності. Цей випадок далі буде згадуватись, як задача керування 2.

В задачах керування 1 та 2 цілеспрямований вплив на об’єкт керу-вання здійснюється перемиканням регулювального відгалуження трансформатора T₂ в межах допустимих положень. Оскільки можливих рішень по одній взятій ЕПУ може бути багато, а у вузлі навантаження таких установок декілька і при визначенні оптимального рішення слід забезпечити ряд технічних та технологічних вимог, то процес знаходження вектора керування має бути автоматизованим.

Для задачі керування 1 за критерій ефективності математичної моделі можна взяти реактивну потужність в лінії живлення групи ЕПУ, для якої необхідно забезпечити мінімальне значення.

Обмеження математичної моделі мають забезпечити для кожної ЕПУ:

– хід технологічного процесу та умови пропускної здатності трансформаторів T₁, T₂ і обмеження за наявною потужністю;

– недопустимість появи по лінії живлення зворотних перетоків реак-тивної потужності із мереж підприємства в мережі енергопостачальної компанії;

– можливість реалізації лише одного положення регулювального відгалуження.

Для знаходження оптимального рішення для задачі керування 1 мо-жна скористатись такою математичною моделлю цілочислового програмування:

де Q – реактивна потужність вузла навантаження електропічних установок, що відповідає вихідному режиму;

ΔQ_nv – приріст реактивної потужності БСК n-ої електропічної установки при перемиканні регулювального відгалуження з положення в положення v.

Математична модель потребує знаходження таких положень регулювальних відпайок T₂ на всіх ЕПУ в межах їх допустимих змін , яким відповідає мінімальне споживання реактивної потужності підприємством. Тобто математична модель (3.12) розроблена так, що в процесі пошуку оптимального вектора керування перебираються лише допустимі із зазначених умов відгалуження компенсаційних трансформаторів T₂ і тим самим забезпечується перше із зазначених технічних обмежень. Обмеження-нерівність математичної моделі виключає можливість отримання таких розв’язків, коли реактивна потужність змінює свій знак, тобто, спрямована з мережі підприємства в мережу енергопостачальної компанії. Математична модель лінійна і для її аналізу можна застосувати класичний симплекс-алгоритм.

Математична модель, за якою можна прийняти технічне рішення для задачі керування 2, має вигляд:

де – вектор струму зворотної послідовності в живильній лінії до прийняття рішення;

Δa_nv; Δb_nv – дійсна та уявна частини вектора струму зворотної послідовності, яка відповідає реактивній потужності, що генерується при перемиканні РПН компенсаційного трансформатора T₂ n-ої електропічної установки з положення у положення v.

Математична модель (3.13) відноситься до класу нескалярних і потре-бує знаходження такого розв’язку, якому відповідає мінімальне зна-чення струму зворотної послідовності в живильному вводі. При цьому можливі режими, коли за математичною моделлю (3.13) будуть знайдені розв’язки, реалізація яких буде супроводжуватись зворотним перетоком реактивної потужності з мереж підприємства в мережі енергопостачальної компанії. Якщо такі випадки можуть мати місце, то математична модель має містити відповідне обмеження на реактивну потужність вузла навантаження. Слід зазначити, що ефект симетрування досягається за рахунок збільшення реактивної потужності технологічних БСК і тому реалізація вектора керування, знайденого за моделлю (3.13), буде супроводжуватись компенсацією реактивної потужності по підприємству.

Режими в мережах електродного заводу динамічні. Протягом доби вони можуть скластися такими, коли має місце велике споживання реактивної потужності. В такій ситуації керівне рішення знаходиться за математичною моделлю (3.12) і додаткова потужність технологічних БСК використовується для компенсації реактивних навантажень. Якщо склався режим, який характеризується суттєвою несиметрією напруг, то для прийняття керівного рішення використовується математична модель (3.13), але при цьому ефект симетрування супроводжується компенсацією реактивної потужності.

Сам процес керування відбувається за такою схемою:

– щогодини диспетчер-електротехнолог встановлює регулювальні відгалуження на трансформаторах T₁ та T₂ по всіх ЕПУ, які забезпечують хід технологічного процесу;

– збирається необхідна інформація про параметри режиму ЕПУ;

– розраховуються вектора керування за математичною моделлю (3.12) або (3.13) для групи працюючих ЕПУ;

– відповідно до отриманих результатів виконуються перемикання відгалужень на компенсаційних транформаторах T₂ (коригується положення, які попередньо були виставлені з міркувань забезпечення технології).

Про ефективність використання технологічних БСК ЕПУ для оптимізації режиму електроспоживання можна зробити висновки, проаналізувавши результати прикладу 3.2.

ПРИКЛАД 3.2. Характеристики ЕПУ для деякого режиму, який склався на одному із реальних електродних виробництв, наведені в табл 3.3.

Пічний трансформатор T₁ та компенсаційний T₂ на всіх ЕПУ ЭОЦН–14000/35.

Знайти вектор керування по кожній ЕПУ, використавши додаткову потужність технологічних БСК для симетрування режиму в мережі.

РОЗВ’ЯЗАННЯ. За попередніми розрахунками множини допустимих до реалізації регулювальних відгалужень (ζn ÷ τn) сформуємо вектори керування по кожній ЕПУ:

Математична модель (3.13) в числовому вигляді для задачі, що вирішується, має вигляд:

де n₁ – одинична рядкова матриця вимірністю 1×14;

n₂ – одинична рядкова матриця вимірністю 1×4;

n₃ – одинична рядкова матриця вимірністю 1×18.

Аналіз отриманої нескалярної математичної моделі за алгоритмом (див. рис. 2.3) дає такі розв’язки:

Отримані розв’язки практично реалізуються так:

ЕПУ1 – на компенсаційному трансформаторі T₂ реалізувати відгалу-ження 2 (замість реалізованого нульового);

ЕПУ2 – ніяких дій не виконувати;

ЕПУ3 – ніяких дій не виконувати.

В табл. 3.4 наведені вихідні параметри режиму та отримані за результатами керування, де І₂ – струм зворотної послідовності в лінії живлення; a_i – коефіцієнт несиметрії струмів (відношення струму зворотної послідовності до струму прямої) в лінії живлення; e₁ – кут зсуву між векторами струму і напруги в системі прямої послідовності.

Як видно із табл. 3.4, за допомогою БСК, що містяться в схемах ЕПУ і використовуються виключно для забезпечення технологічного процесу, без додаткових капітальних вкладень можна ефективно симетрувати ре-жим та компенсувати реактивну потужність на електродному заводі.

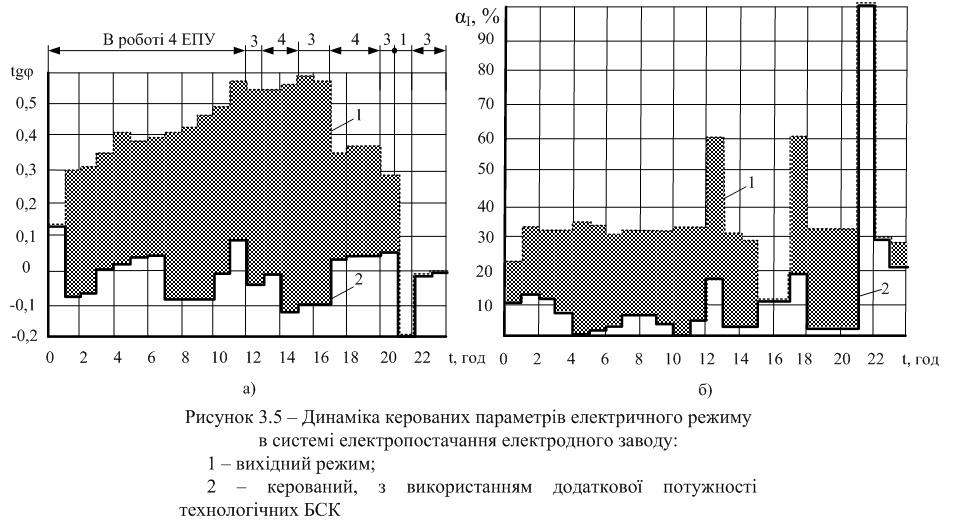
Результати добового керування реактивною потужністю та несиметрією режиму на основі математичної моделі (3.13) зображені на рис. 3.5.