Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
2.4.2 Застосування доповнення до р
Для двох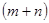 
-розрядних чисел, заданих в системі числення з основою р, обчислимо значення
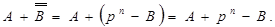
а) Якщо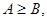 
то 
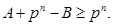
Це означає, що виникає перенесення. Опускаючи ймовірність перенесення (відкидання перенесення), отримаємо
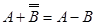(результат додатній).
б) Якщо А < В, то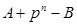 
< 
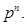
Це означає, що перенесення не виникає. Обчисливши доповнення до р для виразу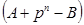 
зі знаком мінус, отримаємо:
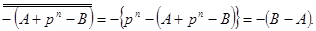
Для цього випадку
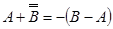(результат від’ємний).
Осмислення вищенаведеного дозволяє реалізувати операцію віднімання двох додатних чисел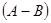 
із застосуванням наведених в пунктах а) і в) правил.
Приклади.
1. Для двох десяткових чисел А = 29 і В = 38 обчислити вирази 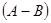і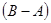 
із застосуванням десяткового доповнення:
а)
А – В в) В – А
+ 
+
——— ———
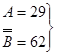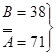0 ← 91 1← ┌ 09
↑ ↓
(перенесення відсутнє) (перенесення не враховується)
↓ ↓
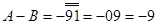
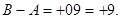
2. Для вказаних чисел, представлених у двійковій системі числення (А = 011101 і В = 100110) обчислити їх різницю із застосуванням двійкового доповнення:
а) А – В б) В – А
+ 
+
————— ———
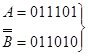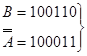0 ← 110111 1← ┌ 001001
↑ ↓
, 
.
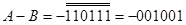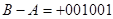3. Для вказаних десяткових чисел, представлених в кодах 8421 і 8421+3, обчислити їх різницю:
а1)
+
—————
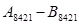
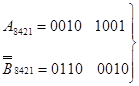1000 1011
+ 0110 (корекція)
—————
0← 1001 0001
↓
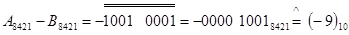
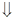
1001 0001
+ 0110 0110 (корекція)
—————
1111 0111
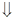
0000 1000
+ 1
—————
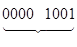
910
б1)
+
—————
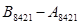
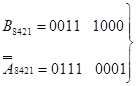1010 1001
+ 0110 (корекція)
—————
1 ← 0000 1001
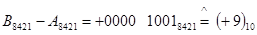
а2)
+
—————
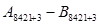
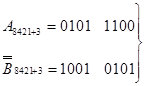0↰ 1↰
1111 0001
+ 1101 0011 (корекція)
—————
1← 1100 0100
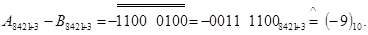
б2)
+
—————
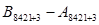
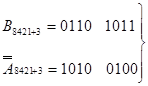┌ 1 ↰ 0↰
0000 1111
+ 0011 1101 (корекція)
—————
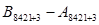= + 0011 1100 