Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

4.2 Прямий код

Самим простим машинним кодом є прямий код, у якому знак числа кодується нулем (додатні числа) і одиницею (від’ємні числа), а цифрова частина числа залишається без змін. Тобто прямим кодом від’ємного числа називається його зображення у звичайній формі запису, у якому в знаковому розряді ставиться одиниця. Прямий код додатного двійкового числа співпадає з його звичайним зображенням у природній формі, тому що знак кодується нулем.

Згідно визначенню, функція кодування чисел в прямому коді для правильних дробів вигляду: 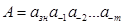 запишеться таким чином:

 

(4.1)

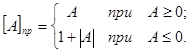
Величина числа А буде визначатись в прямому коді таким виразом:

 

(4.2)

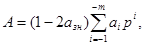
при цьому знаковому розряду не приписується ніякої ваги. 

Очевидно, що діапазон зміни машинних зображень для прямого коду лежить в межах

 

(4.3)

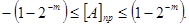
Приклад. Записати числа  A = + 0,1000110101101101  i B = - 0,0111010110010101 в прямому коді:

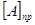 = 0,1000110101101101;

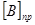= 1,0111010110010101.

В прямому коді нуль має два значення: додатне 0,000... і від’ємне 1,000... Звичайно в ЕОМ використовується додатній нуль, але в процесі обчислення може виникнути і його від’ємне зображення. Ці зображення повністю еквівалентні і використання будь-якого з них не приводить до помилки.