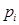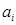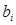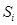Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

5 ВИКОНАННЯ АРИФМЕТИЧНИХ ОПЕРАЦІЙ ДОДАВАННЯ І ВІДНІМАННЯ В КОДАХ

5.1 Основні поняття

Важливою функцією багатьох цифрових пристроїв і МП є виконання арифметичних операцій додавання і віднімання. В зв’язку з цим в ЕОМ і МП виділяють спеціальний функціональний блок – арифметичний пристрій (АП), призначений для виконання операцій над числовими кодами. Числа, які беруть участь в арифметичних операціях, називаються операндами.

Для позиційних систем числення із звичайною вагою всі допустимі числа є поліномами із степенями р (основи системи числення). Отже, всі арифметичні діі в цьому випадку виконуються за правилами алгебраїчного додавання поліномів.

Додавання двійкових чисел виконується у відповідності з правилами, визначеними у розділі 2.2 (таблиця 2.1). Але необхідно врахувати, що фактично у порозрядному додаванні приймають  участь не дві, а три цифри. Третім доданком є цифра перенесення з сусіднього молодшого розряду (див. (2.8)). Таблиця додавання у цьому випадку буде мати вигляд, представлений у табл.5.1.

Кожна сума у таблиці 5.1 записана двома розрядами, молодший з яких є безпосередньо сума у поточному 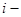му розряді, а старший – цифра перенесення у наступний старший розряд  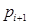(значення цього розряду продубльовано у останньому стовпці таблиці 5.1).

При обчисленні суми двох чисел можливі два випадки: доданки мають однакові знаки; доданки мають різні знаки. У відповідності з цим алгоритми одержання суми для кожного з варіантів значно відрізняються між собою. Так, спрощений алгоритм додавання двох чисел з однаковими знаками можна визначається таким чином:

- додати два числа;

- сумі присвоїти знак одного із доданків.

Алгоритм одержання алгебраїчної суми можна записати таким чином:

- порівняти знаки доданків і, якщо вони однакові, то виконувати додавання за першим алгоритмом;

- порівняти доданки за абсолютною величиною, якщо знаки доданків різні;

- якщо є необхідність, переставити числа місцями (щоб віднімати від більшого менше);

- провести віднімання двох чисел;

- результату присвоїти знак більшого доданку.

З цього випливає, що перший алгоритм значно простіший другого. Отже, бажано перетворити від’ємні числа таким чином, щоб операцію віднімання замінити додаванням, тобто виконати додавання двох чисел таким чином:

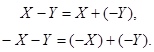
Для цього необхідно зобразити додатні та від’ємні числа єдиним натуральним кодом, що можливо досягти при використанні систем числення з додатньою основою та симетричною базою або з від’ємною основою та невід’ємною базою. При використанні однорідних позиційних систем числення з додатньою основою та невід’ємною базою натуральним кодом можна представити тільки додатні числа та нуль, тобто в цьому випадку не існує єдиного натурального коду для додатніх та від’ємних чисел. Це приводить до того, що проблему представлення чисел зі знаком приходиться вирішувати на рівні слів за допомогою спеціальних кодів: прямого, оберненого та доповняльного, визначення яких наведено у главі 4.