2.1.2   Основні означення статики

Означення 1. Точка перебуває у стані рівноваги, якщо вона перебуває у спокої або рухається рівномірно і прямолінійно в інерціальній системі відліку.

Наслідок. Коли кожна точка системи матеріальних точок перебуває в стані рівноваги, то і система в цілому буде в стані рівноваги (state of equilibrium).

Означення 2. Сукупність сил , , , … , прикладених до тіла або до точки, називається системою сил (system of force) і позначається .

Означення 3. Система сил  називається зрівноваженою (balanced) або еквівалентною нулю (нульовою системою), якщо система матеріальних точок під її дією перебуває в стані рівноваги. Символічно нульову систему позначають так:

.                                          (2.1)

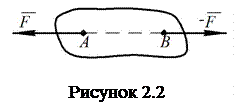
Наслідок 1. Дві сили, що діють на абсолютно тверде тіло, зрівноважені тоді і лише тоді,коли вони діють уздовж спільної лінії дії в протилежному напрямі і мають однакове числове значення (рис. 2.2).

Наслідок 2. Система матеріальних точок перебуватиме у стані рівноваги, якщо до неї прикласти або від неї відкинути зрівноважену систему сил.

Означення 4. Не змінюючи стану руху  абсолютно твердого тіла, силу можна переносити уздовж її лінії дії в довільну точку тіла.

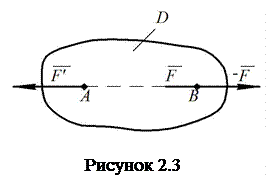
До тіла  у точці  (рис. 2.3) прикладена силу . Візьмемо на лінії дії цієї сили довільну точку  і прикладемо в цій точці дві сили, що дорівнюють силі  і напрямлені у протилежні боки вздовж її лінії дії.

Таку систему сил можемо прикласти, не порушуючи рівноваги на підставі означення 3 і наслідків із нього. Сила , прикладена в точці , і сила , прикладена в точці , зрівноважені. На підставі наслідку 2 (означення 3) таку систему можна відкинути, не порушуючи рівноваги тіла. Отже, залишається сила , прикладена в точці . Таким чином, означення 4 є очевидним.

Означення 5. Дві системи сил  і  називаються зрівноваженими одна відносно одної, якщо їх сукупність утворює зрівноважену систему (нульову), тобто

                                       (2.2)

Означення 6. Дві системи сил  і  називаються статично еквівалентними, якщо кожна з них окремо зрівноважує одну й ту саму третю систему сил :

                                            (2.3)

якщо

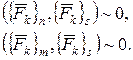                                       (2.4)

Означення 7. Якщо система сил  статично еквівалентна одній силі , то вона називається рівнодійною системи сил: