2.2.10  Теорема еквівалентності

Дві системи сил  і  мають головні вектори ,  і головні моменти (,) систем відносно довільної точки .

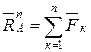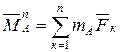,  ,                                        (2.53)

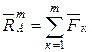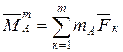, .                                        (2.54)

Означення. Дві системи сил  і  еквівалентні, якщо їх головні вектори і головні моменти відносно довільної точки однакові.

Нехай системи сил  і  еквівалентні:

                                                      (2.55)

Тоді з означення еквівалентних систем (2.4) матимемо

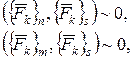                                                   (2.56)

де система сил  є зрівноважуючою відносно системи сил  і .

Знайдемо головний вектор  і головний момент системи сил  відносно точки :

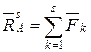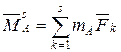, .                                   (2.57)

   Із умов (2.56) і аксіоми рівноваги з урахуванням (2.53), (2.54), (2.57) випливають такірівності:

,  .                               (2.58)

,  .                               (2.59)

Порівнюючи перші та другі рівності відповідно систем (2.58) і (2.59), знаходимо

, ,                                       (2.60)

що і треба було довести.

Наслідок. Якщо у двох системах сил  і  головні вектори і моменти систем відносно довільної точки  однакові, то ці системи еквівалентні.

Візьмемо систему , яка є зрівноважуючою щодо системи сил, наприклад, . Тоді виконуватимуться умови (2.59), розглянувши які разом із рівностями (2.60) матимемо умови (2.58). Таким чином, система  є зрівноважуючою відносно двох систем  і , тобто справедливі умови (2.56). Звідки маємо, що системи сил  і  еквівалентні (2.55).