2.2.2 Аксіома рівноваги

Означення. Система сил  буде врівноваженою, якщо головний вектор  і головний момент системи  відносно довільного центра дорівнюватимуть нулю:

, .                                         (2.23)

Умови (2.23) у проекціях на декартові осі координат запишуться у вигляді

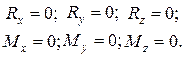                                 (2.24)

Аксіома рівноваги для збіжної системи сил

Означення. Система сил називаються збіжною (convergent), якщо лінії дії всіх сил перетинаються в одній точці (рис. 2.8).

Нехай головний вектор системи дорівнює нулю:

.                                                     (2.25)

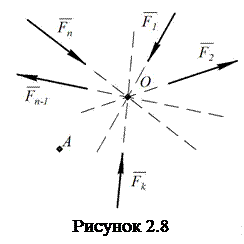Із означення моменту сили відносно центра для збіжної системи сил маємо:

.                       (2.26)

Візьмемо у просторі довільну точку  (рис. 2.8) і за теоремою про зв’язок між головними моментами системи відносно різних центрів знайдемо:

.             (2.27)

Розглянувши рівність (2.27) разом із (2.26) і (2.25), побачимо, що . Таким чином, збіжна система сил буде врівноважена, якщо її головний вектор дорівнюватиме нулю.

Умова (2.25) аналогічна трьом скалярам:

                                         .                            (2.28)

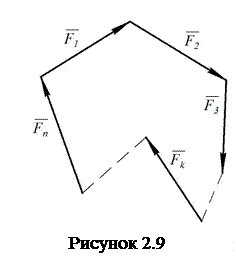Із виразу (2.25) виходить, що для збіжної врівноваженої системи сил силовий многокутник, побудований на силах, як на сторонах, буде замкненим (рис. 2.9).

Якщо лінії дії врівноваженої системи сили лежать в одній площині, то умову (2.28) записують у вигляді двох рівнянь, наприклад, для площини 

.                    (2.29)

Аксіома рівноваги для системи паралельних сил

Розглянемо систему сил , у якій лінії дії всіх сил паралельні.

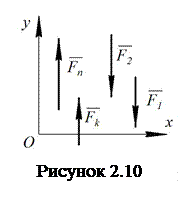
Введемо декартову систему таким чином,  щоб вісь z була паралельна векторам сил (рис. 2.10).

Аналізуючи рівняння (2.24) для врівноваженої довільноїпросторової системи сил, одержимо умови, за яких системапаралельних сил буде врівноваженою:

     .                 (2.30)

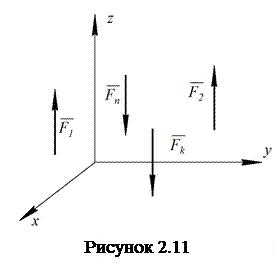
Якщо лінії дії всіх сил лежать в одній площині, наприклад  (рис. 2.11), то умови (2.30) запишуться у вигляді (якщо сили паралельні осі ):

, .                 (2.31)

         Аксіома рівноваги для плоскої системи сил

Умови (2.24) для системи сил, лінії дії яких довільно розміщені в одній площині (рис. 2.12), мають вигляд

, , .                     (2.32)

Три незалежні рівняння для плоскої системи сил можна записати інакше:

, , .                        (2.33)

, , .                       (2.34)

Але при цьому на вибір точок, відносно яких знаходять головний вектор системи, накладаються умови: точки  і  (2.33) не повинні лежати на прямій, перпендикулярній до осі ; точки ,  і  (2.34) не повинні лежати на одній прямій.