2.2.3 Теорема про три непаралельні сили

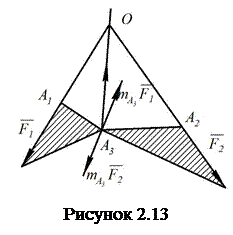
Означення. Якщо під дією трьох непаралельних сил тіло знаходиться у стані рівноваги, то лінії дії сил лежать в одній площині і перетинаються в одній точці.

Нехай на тіло діє врівноважена система сил  (рис. 2.13).

.

Знайдемо головний момент системи відносно точки  (точки прикладання сили ).Ураховуючи умови (2.33), маємо

          .                       (2.35)

Сума двох векторів дорівнюватиме нулю, якщо вони напрямлені по одній прямій, однакові за величиною і протилежні за напрямом.

Таким чином, із умови (2.35) виходить, що сили  і  лежать у одній площині. Оскільки сили  і  непаралельні, то їх лінії перетнуться в точці . Знайдемо головний момент системи  відносно точки :

.                                    (2.36)

Лінії дії сил  і  проходять через точку , тоді

, .                                       (2.37)

І з (2.36) випливає, що .

Це означає, що лінія дії сили  проходить через точки  і , які лежать у площинісил  і . Таким чином, сили ,  і  лежать у одній площині і лінії їхперетинаються в точці .