2.2.8 Сили тертя ковзання

До невільного тіла  з шорсткою поверхнею прикладена система сил  (рис. 2.21).

У точці  тіло має геометричний дотик шорсткої поверхні тіла , яка відносно тіла  єв’яззю. Нехай в точці  прикладена рівнодійна 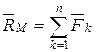 системи сил .

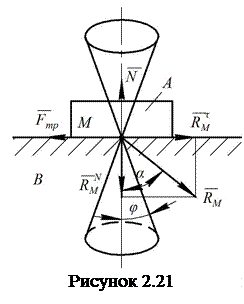Розкладемо силу  на складові  і , напрямлені по спільній нормалі до поверхні тіла ,  і по дотичній. Нормальна складова  притискує тіло  до площини  і спричинює нормальну реакцію . Дотична складова  може спричинити рух тіла  в напрямі спільної дотичної до поверхонь тіл  і . Наявність або відсутність руху тіла залежить від співвідношення між дотичною складовою сили  і найбільш можливою величиною – дотичною реакцією в’язі , яка називається силою тертя (frictionforce).

Сили тертя виникають не тільки між поверхнями твердих тіл, які і вважаються вільними від змащування, а й між частинками рідин і газів при їх внутрішніх взаємодіях та з поверхнями твердих тіл.

Залежно від взаємних рухів, тертя між твердими тілами є трьох видів. У тих випадках, коли, відносна швидкість точок дотику поверхонь тіл, які контактують, не дорівнює нулю, виникає тертя ковзання (kinetic friction) або тертя першого роду. Якщо відносна швидкість точок дотику поверхонь дорівнює нулю і спостерігається кочення без ковзання, виникаєтертя кочення (rolling friction) або тертя другого роду. Нарешті розглядають тертя третього роду або тертя крутіння (pivoting friction).

Уперше тертя ковзання вивчив на дослідах Амонтон, а властивості сил тертя сформулював видатний фізик Кулон.

Як свідчать навіть найпростіші досліди, сила тертя спокою (при відсутності відносного руху тіл  і , рис. 2.21) має неозначений напрям і величину. Сила тертя ковзання – гальмуюча. Вона має напрям, протилежний напряму того руху тіла, що міг би виникнути під дією активних сил , коли б сила тертя перестала чинити опір цьому руху.

Дослідження сил тертя ковзання, привели до таких результатів:

1.  Сила тертя ковзання залежить від матеріалу та фізичного стану поверхонь тертьових тіл;

2.  Тертя руху майже не залежить від відносної швидкості між тертьовими тілами;

3.  Сила тертя спокою завжди більша, ніж сила тертя руху;

4.  Тертя зростає при збільшенні часу попереднього контакту між поверхнями тіл;

5.  Величина сили статичного тертя задовольняє нерівність

,                                                (2.38)

де  – коефіцієнт пропорційності, який називається коефіцієнтом статичного тертя ковзання.

Знак рівності відповідає стану граничної рівноваги між силою тертя і активними силами:

                                                 .                                               (2.39)

Позначимо кут між силами  і  через  (див. рис. 2.21). Тоді модулі векторів  і запишуться у вигляді

, .

   Отже, на підставі (2.38) і (2.39), якщо

,                                      (2.40)

тоді тіло перебуває в стані рівноваги. Знак рівності відповідає стану граничної рівноваги. Коли справджується нерівність

                               ,                                           (2.41)

тіло рухається. Нерівність (2.41) можна записати у вигляді

.                                                    (2.42)

Уведемо кут тертя  так, що . Отже, якщо , то тіло перебуває в стані рівноваги, а коли , тіло рухається.

Проведемо через точку  (див. рис. 2.21) пряму під кутом  до спільної нормалі поверхонь тіл  і . Обертаючи цю пряму навколо нормалі, одержимо поверхню конуса з кутом  при вершині. Цей конус називається конусом тертя. Якщо сила  проходить у середині конуса тертя, то тіло  перебуває в стані рівноваги при будь-яких значеннях сили . Якщо вектор  напрямлений по твірній конуса тертя, тіло  перебуває в стані граничної рівноваги. І у випадку, коли вектор  проходить поза конусом тертя, тіло  рухається.

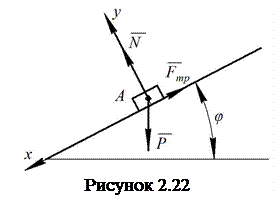
Приклад. На  шорсткій площині, нахиленій під кутом  до горизонту, лежить тіло ,вага якого  (рис. 2.22).

Коефіцієнт статичного тертя ковзання цього тіла об похилу площину дорівнює . Знайти максимальне значення кута , при якому тіло  буде знаходитись у стані рівноваги.

Розв’язання. Розглянемо граничний стан рівноваги тіла, тобто таке положення  похилої площини, за якого збільшення кута нахилу призведе до руху тіла . На тіло  діє одна активна сила – сила ваги  і накладена в’язь – похила площина.

Згідно з аксіомою про в’язі, дію негладкої похилої площини на тіло  замінюємо реакцією в’язі: нормальною реакцією  і силою тертя                 (рис. 2.22). Запишемо аксіому рівноваги в проекціях на осі і :

; .                          (2.43)

; .                         (2.44)

На підставі формули (2.39)

.                                           (2.45)

Із виразів (2.43) – (2.45) знаходимо кут  при граничному стані рівноваги тіла  на похилій площині  або .