2.2.9 Тертя кочення

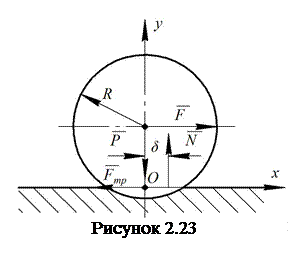
Розглянемо абсолютно твердий циліндричний каток вагою , що спирається на горизонтальну здеформовану площину і на який діє горизонтальна сила  (рис. 2.23).

При малих значеннях сили  каток перебуватиме в стані рівноваги. При збільшенні сили у певний момент матимемо граничний стан рівноваги, а далі каток рухатиметься.

Припустимо, що каток перебуває в стані граничної рівноваги. Візьмемо до уваги деформацію площини, на яку спирається каток. Дію площини на каток замінимо нормальною силою  і силою тертя  (рис. 2.23). Тоді з умови рівноваги системи сил на площині маємо:

                                        ; ,                                       (2.46)

                                        ; ,                                        (2.47)

                                        ; .                                 (2.48)

Зміщення реакції площини  на величину  в напрямі можливого руxy тіла пояснюється деформацією площини, на яку спирається каток.

Розглянемо поняття моменту тертя кочення при граничному стані рівноваги:

.                                             (2.49)

Величина  називається коефіцієнтом тертя кочення і має розмірність довжини.

Із рівностей (2.46) – (2.49) знайдемо коефіцієнт тертя кочення:

 ,                                                (2.50)

і зв’язок між силою  нормальною реакцією :

.                                                (2.51)

Якщо сила  невелика і каток знаходиться в стані рівноваги, то рівняння (2.49) і (2.51) можна замінити нерівностями:

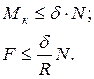                                              (2.52)

У довідкових таблицях наведено відношення коефіцієнта тертя кочення до радіуса циліндра () для різних матеріалів.