2.4.2 Два інваріанти зведення системи сил до центра

Відомо, що головний вектор довільної системи сил 

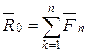,                                              (2.73)

не залежить від центра зведення. Головний момент системи, а отже і момент результуючої пари, змінюється залежно від центра зведення:

,                                            (2.74)

де  і   – момент результуючої пари при зведенні довільної системи сил відповідно до центрів  і .

Другий доданок у правій частині формули (2.74) являє собою момент результуючої сили, прикладеної в центрі , відносно нового центра зведення .

Помножимо скалярно ліву і праву частини рівності (2.74) на вектор :

.                             (2.75)

Оскільки  і вектор  перпендикулярний до вектора , то їх скалярнийдобуток дорівнює нулю. Таким чином,

.                                               (2.76)

Тобто, при зміні центра зведення не змінюється результуюча сила і скалярний добутокрезультуючої сили на момент результуючої пари. Ці величини є інваріантними відносновибору центра зведення.

Першим статичним інваріантом називається результуюча сила

.

Другим статичним інваріантом називається скалярний добуток результуючої сили намомент результуючої пари:

.                                    (2.77)

Запишемо (2.76) в такому вигляді:

.

Якщо результуюча сила не дорівнює нулю, то

.

При зміні центра зведення проекція моменту результуючої пари на напрям результуючої сили не зміниться.