2.4.3 Деякі випадки зведення довільної системи сил

І. При зведенні системи сил  до центра  з’ясувалось, що момент результуючої пари дорівнює нулю. Тоді система сил  буде замінена однією результуючою силою, тобто

.                                                (2.78)

Означення. Якщо система сил  замінюється однією силою, то така сила називається рівнодійною.

Якщо умова (2.78) виконується, то відповідно до теореми еквівалентності запишемо

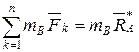 ,                                                (2.79)

де  – довільна точка простору.

Означення. Момент рівнодіючої системи сил відносно довільного центра дорівнює векторній сумі моментів сил системи відносно того самого центра (теорема Варіньона).

ІІ. Система сил при зведенні до деякого центра  замінюється однією парою з моментом . Тоді згідно з (2.22) маємо

 ,                                              (2.80)

де точка  – новий центр зведення. Оскільки , то  також дорівнює нулю і виходить, що момент результуючої пари не залежить від вибору центра зведення:

.

Таким чином, система сил  зводиться до рівнодіючої пари, момент якої не залежить від вибору центра.

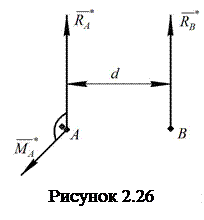
ІІІ. Систему сил  можна замінити однією результуючою силою  і результуючою парою , причому вектор сили лежить  у  площині  пари,  тобто     (рис. 2.26).

Відповідно до правила паралельного перенесення сили сукупність пари і сили, що лежать у площині пари, можна замінити однією силою, переміщуючи її в площині пари у відповідну сторону на величину

.

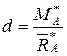Означення. Якщо система сил зводиться до результуючої пари і сили, що лежить у площині пари, то ця система зводиться до рівнодійної сили.

ІV. Головний вектор і головний момент системи сил  відносно центра  відмінні від нуля, причому площина пари перпендикулярна до вектора сили.

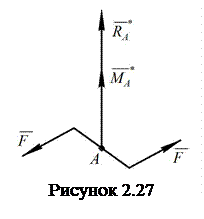
Означення. Сукупність результуючої сили і результуючої пари сил системи , у якій площина пари перпендикулярна до           вектора сили, називається динамо, або                    гвинтом (рис. 2.27).