2.4.4 Теорема зведення системи сил до найпростішого вигляду
Розглянуті чотири випадки зведення довільної системи сил показали, що зміна центра зведення може привести до спрощення або ускладнення системи, яку отримуємо в результаті зведення.
Означення. При
зведенні довільної системи сил ![]() до
найпростішого вигляду вона зводиться до динами.
до
найпростішого вигляду вона зводиться до динами.
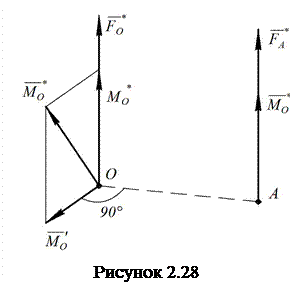 Нехай у
довільному центрі зведення
Нехай у
довільному центрі зведення ![]() система
зведена до сили
система
зведена до сили ![]() , яка
дорівнює головному вектору
, яка
дорівнює головному вектору і
парі сил з моментом
і
парі сил з моментом ![]() (рис.
2.28), який дорівнює головному моменту системи відносно центра
(рис.
2.28), який дорівнює головному моменту системи відносно центра
 .
.
Причому другий інваріант системи відмінний від нуля, тобто
![]() .
.
Розкладемо момент результуючої пари на
дві складові: одну ![]() направимо
по результуючій силі, а другу
направимо
по результуючій силі, а другу ![]() –
перпендикулярно до результуючої сили.
–
перпендикулярно до результуючої сили.
Сукупність пари ![]() і
сили
і
сили ![]() ,
що лежить у площині пари, відповідно до правила паралельного перенесення сил
можна замінити однією силою
,
що лежить у площині пари, відповідно до правила паралельного перенесення сил
можна замінити однією силою ![]() паралельним
перенесенням її у відповідний бік на величину
паралельним
перенесенням її у відповідний бік на величину ![]() .
Оскільки пару сил з моментом
.
Оскільки пару сил з моментом![]() можна
переміщувати у площині пари, то
можна
переміщувати у площині пари, то ![]() .
.
Таким чином,
![]() .
.
Із рис. 2.28 видно, що сила ![]() перпендикулярна
до площини пари з моментом
перпендикулярна
до площини пари з моментом ![]() ,тобто
ми одержали динамічний гвинт або динамо.
,тобто
ми одержали динамічний гвинт або динамо.
Точка ![]() не
єдина, де система сил зводиться до динами. Силу
не
єдина, де система сил зводиться до динами. Силу ![]() можна
переносити вздовж лінії її дії, а момент пари сил є вільним вектором. Таким
чином, систему сил можна звести до динамічного гвинта в усіх точках прямої, яка
проходить через точку
можна
переносити вздовж лінії її дії, а момент пари сил є вільним вектором. Таким
чином, систему сил можна звести до динамічного гвинта в усіх точках прямої, яка
проходить через точку ![]() і
є лінією дії сили
і
є лінією дії сили ![]() . Ця
пряма називається центральною віссю системи сил. Знайдемо тепер рівняння
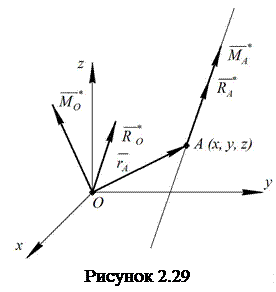
центральної осі. Нехай
. Ця
пряма називається центральною віссю системи сил. Знайдемо тепер рівняння
центральної осі. Нехай ![]() (рис.
2.29) – точка центральної осі.
(рис.
2.29) – точка центральної осі.
 За теоремою
про зв’язок між головними
моментами сил відносно різних центрів маємо
За теоремою
про зв’язок між головними
моментами сил відносно різних центрів маємо
![]() ,
,
Звідки
![]() . (2.81)
. (2.81)
Умову колінеарності ![]() і
і ![]() запишемо
у вигляді
запишемо
у вигляді
![]() , (2.82)
, (2.82)
де ![]() – скалярний
множник, який називатимемо параметром гвинта.
– скалярний
множник, який називатимемо параметром гвинта.
Нехай ![]() ,
, ![]() ,
, ![]() і
і ![]() ,
, ![]() ,
, ![]() –
відповідно проекції головних вектора і моменту на осі
–
відповідно проекції головних вектора і моменту на осі ![]() ,
, ![]() ,
, ![]() ,
тоді
,
тоді
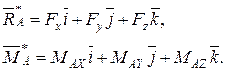 (2.83)
(2.83)
Тепер рівність (2.82) з урахуванням (2.83) запишемо у вигляді
![]()
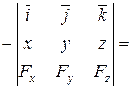 (2.84)
(2.84)
![]()
де ![]() ,
, ![]() ,
, ![]() –
координати точки
–
координати точки ![]() центральної
осі.
центральної
осі.
Порівнюючи коефіцієнти при одиничних
векторах ![]() ,
, ![]() ,
, ![]() матимемо
матимемо
![]() ;
;
![]() ;
;
![]() .
.
Отже
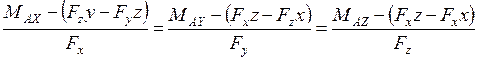 .
.
Це і є рівняння центральної осі системи сил.