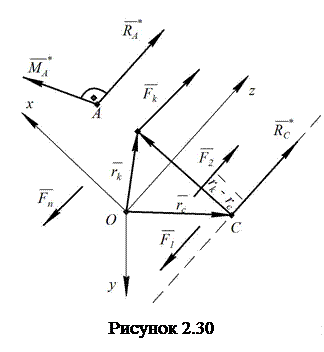
2.4.5 Випадок зведення до центра і найпростішого вигляду системи паралельних сил

Розглянемо систему паралельних сил , в якій головний вектор і головний момент відносно довільного центра відмінні від нуля (рис. 2.30). Введемо систему координат так, щоб вісь  була паралельна силам. Знайдемо другий інваріант системи:

,                        (2.85)

де , ,  і , ,  – відповідно проекції результуючої сили і моменту результуючої пари на осі , , , як видно з рис. 2.30.

; ; ;

; ; .

Тоді з (2.85) отримуємо

                  .                                       (2.86)

Оскільки за умовою головний вектор і головний момент системи відмінні від нуля, то рівність (2.86) виконуватиметься, якщо сила  лежатиме в площині пари з моментом . Така сукупність відповідно до правила паралельного перенесення сили зводиться до однієї сили, що дорівнює головному вектору системи.

Таким чином, система паралельних сил зводиться до рівнодійної, якщо головний вектор системи не дорівнює нулю.

Знайдемо радіус-вектор точки , яка лежить на лінії дії рівнодійної.

Відповідно до теореми Варіньона (2.80) сума моментів усіх сил відносно точки  дорівнює нулю:

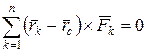,                                        (2.87)

оскільки точка  лежить на лінії дії рівнодіючої  (рис. 2.30).

Рівність (2.87) можна переписати в такій формі:

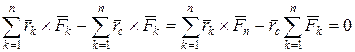.             (2.88)

Введемо одиничний вектор , паралельний лініям дії сил. Тоді довільну силу  можна записати у вигляді

,                                           (2.89)

де , якщо напрям сили збігається з напрямом вектора , , якщо сила  і вектор  напрямлені протилежно.

Тоді

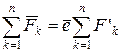.                                    (2.90)

Підставляючи вирази (2.89) і (2.90) у співвідношення (2.88), маємо

,

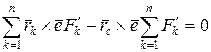звідки

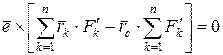.                                (2.91)

Рівність (2.91) виконується при довільному напрямі сил тільки за умови, що перший множник дорівнює нулю:

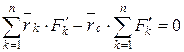,                                      (2.92)

звідки

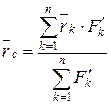   .                                           (2.93)

Нехай , ,  – координати центра паралельних сил, а , ,  – координати точки прикладення довільної сили . Тоді координати центра паралельних сил можна визначити за формулами

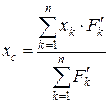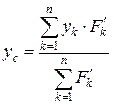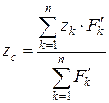, ,  .                  (2.94)

Ураховуючи те, що точка  не залежить від орієнтації паралельних сил у просторі, можна сказати, що центр паралельних сил є точкою простору, навколо якої повертається рівнодійна система паралельних сил при повороті всіх сил на один і той самий кут в один бік навколо точок їх прикладення.