

Мета роботи: Ґрунтуючись на великій кількості спостережень дос-ліджуваної величини, визначити її найбільш достовірне розрахункове значення і закон розподілу експериментальних даних, а також перевірити узгодженість теоретичного та реального розподілів.
Обладнання, пристрої та інструменти: нормативна, навчальна та довідкова література.
Визначення закону розподілу випадкової величини виконується стандартними методами обробки масивів статистичних даних. Порядок розрахунків наведено нижче.
2.1 Побудова гістограми розподілу
Масив експериментальних даних (випадкових величин) розбивається на кілька інтервалів. Для визначення оптимальної величини інтервалу використовується залежність:
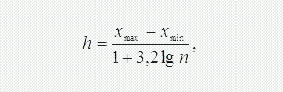
де хmax , х min – відповідно максимальне й мінімальне значення експери-ментальної величини;
п – кількість дослідних даних.
Рекомендована кількість інтервалів для пропонованих варіантів приймається рівною 7–8. Бажано, щоб всі значення потрапили в інтервали.
Після цього необхідно підрахувати число появи експериментальної величини в даному інтервалі(mN), ймовірність потрапляння (R N ) та щільність розподілу (P N ). Вибірку доцільно зробити у вигляді таблиці 2.2, як у прикладі розв’язання (далі).
Для побудови гістограми розподілу відкласти на осі абсцис чисельні значення границь інтервалів та їхніх середин, тобто х1…х N . По осі ординат – значення щільності РN . Значення щільності відкладати від середини інтервалів, вважаючи, що вона постійна для всього інтервала. Вигляд такої дослідної гістограми наведений на рисунку 2.1в прикладі розв’язання.
2.2 Визначення розрахункового значення досліджуваної величини й теоретичного закону її розподілу
Теоретичним законом розподілу випадкової величини є аналітична залежність між її чисельними значеннями X і щільністю ймовірностей f(x). До найпоширеніших теоретичних законів розподілу випадкових величин відносять нормальний закон розподілу (закон Гаусса) і логарифмічно-нормальний закон розподілу.
Нормальний закон розподілу найбільше часто використовується при визначенні сумарного напрацювання відновлюваних деталей до капітального ремонту, часу відновлення виробів, що ремонтуються, папрацювання до відмови невідновлюваних деталей і має вигляд:
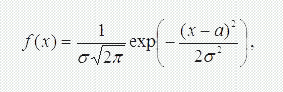
де σ – середньоквадратичне відхилення розподілу випадкової величини х;
а – математичне очікування розподілу випадкової величини.
Логарифмічно-нормальний розподіл широко використається на автомобільному транспорті при дослідженні довговічності й надійності автомобіля, при вирішенні завдань теорії масового обслуговування. Закон має вигляд:
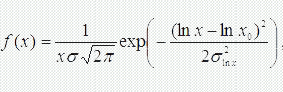
де x0 і σlnx визначаються з виразів:
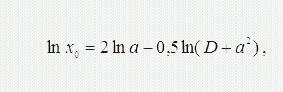
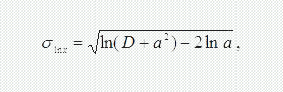
де D – дисперсія розподілу випадкової величини.
Числовими характеристиками випадкових величин є: математичне очікування а, дисперсія D і середньоквадратичне відхилення σ. Найбільш достовірним значенням досліджуваної величини, яке може бути використане надалі при вирішенні практичних завдань, є математичне очікування.
Математичне очікування дискретної величини – це сума добутків її можливих значень на їхню ймовірність, тобто
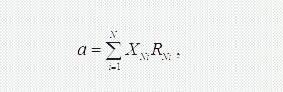
де XNi – середнє значення і-го інтервалу;
RNi – ймовірність потрапляння випадкової величини до і-го інтервалу.
Дисперсія випадкової величини характеризує розсіювання й розкид значень випадкової величини в околі її математичного очікування. Значення дисперсії визначається за формулою:
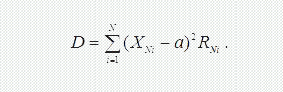
Для наочної характеристики розсіювання зручніше використовувати величину, розмірність якої збігається з розмірністю випадкової величини – середньоквадратичним відхиленням
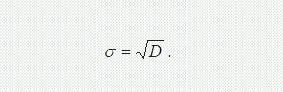
З метою зменшення трудомісткості розрахунків для кожного варіанта пропонується закон розподілу. Необхідно знайти його числові характеристики й перевірити відповідність теоретичному закону.
Розрахунок числових характеристик рекомендується проводити в табличній формі (табл. 2.3в прикладі розв’язання).
На гістограму статичного розподілу нанести графік теоретичного закону розподілу.
Узгодженість між теоретичним і статистичним розподілами оцінюємо за допомогою найбільш розповсюдженого у літературі способу – за критерієм Пірсона – «критерій χ2».
Обчислювальна схема визначення узгодженості за критерієм χ2зводиться до нижченаведеного. Визначають міру розбіжності:
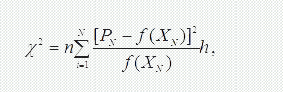
де п – кількість значень у масиві даних;
N – число інтервалів;
PN – щільність розподілу в кожному інтервалі;
h – ширина інтервалу.
Визначають число ступенів свободи rяк різницю між числом інтервалів N і закладених зв'язків (умов)
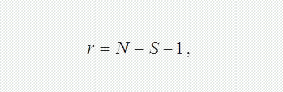
де S– кількість числових характеристик (параметрів) закону розподілу.
Для використовуваних нормального і логарифмічно-нормального розподілів S=2, тоді
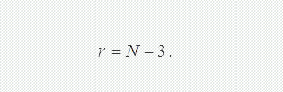
Заrи χ2 за допомогою таблиці 2.1 визначають рівень значимості α теоретичного розподілу.
Якщо α>0,05, то статистичний (експериментальний) розподіл узгоджується з теоретичним. У протилежному випадку зазначені розбіжності будуть не випадковими, а обраний теоретичний закон відкидається. Необхідно для опису даного масиву шукати більш підходящий закон розподілу.
Таблиця 2.1 – Значення χ2 в залежності від r і α

Визначити розрахункові значення середнього пробігу до капітального ремонту (тис. км) автомобіля ГАЗ-31029. Масив передбачається описати нормальним законом розподілу.
1) Визначаємо ширину інтервалу за формулою (2.1).
Масив даних, тис. км:
220, 252, 255, 261, 262, 268, 271, 271, 274, 275, 276, 281, 282, 284, 286, 287, 288, 288, 290, 291, 291, 291, 292, 293, 299, 300, 300, 300, 301, 301, 302, 302,304, 305, 305, 305, 305, 308, 308, 312, 312, 314, 314, 316, 318, 320, 320, 322, 322, 324, 325, 325, 328, 329, 330, 334, 335, 340, 344, 345, 345, 350, 350, 351, 352, 355, 360, 370, 370, 375, 381, 382.
Разом 72 виміри.
Найменше значення: 220 тис. км.
Найбільше значення: 382 тис. км.
Ширина інтервалу, h=21,891090 тис. км.
Приймаємо h = 22 тис. км.
2) Розбиваємо масив експериментальних даних на 8 інтервалів і заповнюємо таблицю 2.2.
Таблиця 2.2 – Параметри статистичного розподілу

За даними таблиці 2.2 креслимо гістограму розподілу (рисунок 2.1).

Рисунок 2.1 – Гістограма емпіричної PN і графік теоретичної f(x) щільності розподілусереднього пробігу до капітального ремонту автомобілів ГАЗ-31029
3) Заповнюємо в таблиці 2.3 характеристики розподілу:
а) математичне очікування (стовпець 4);
б) дисперсія (стовпець 7).
4) Обчислюємо координати теоретичної кривої розподілу в точках середин інтервалів і заносимо в таблицю 2.3 (стовпець 9).
5) Визначаємо критерій узгодження за формулою (2.9), використовуючи стовпець 12, перевіряємо узгодженість теоретичного й статистичного розподілів.
Міра розбіжності
χ2= 72•0,0534 =3,8448.
Визначаємо число ступенів свободи
r = 8 - 2 - 1 =5.
Таблиця 2.3 – Розрахунок числових характеристик й ординат теоретичного закону розподілу та критерію узгодження

Визначаємо, використовуючи таблицю 2.1, рівень значимості α при r=5 та χ2= 3,8448.
Оскількиα = 0,6 > 0,05, то вважаємо гіпотезу узгодженості теоретичного та статистичного розподілів достовірною.
1. Згідно з варіантом, вказаним викладачем, стандартними методами обробки статистичних даних визначити закон розподілу технічного параметра.
Варіанти завдань для виконання лабораторної роботи наведено в таблицях 2.4–2.6.
2. Визначити значення критерію χ2 та рівень значимості α теоретичного розподілу.
3. За результатами розрахунків зробити висновки про узгодженість передбачуваного і дійсного законів розподілу.
Таблиця 2.4 – Варіанти завдань для нормального закону розподілу випадкових величин

Таблиця 2.5 – Варіанти завдань для логарифмічно-нормального закону розподілу випадкових величин

Продовження таблиці 2.5

Таблиця 2.6 – Масив статистичних даних для варіантів завдань

Продовження таблиці 2.6

Продовження таблиці 2.6

Продовження таблиці 2.6

1. Як визначається кількість інтервалів для розбивання масиву?
2. Що таке нормальний закон розподілу? Коли він застосовується?
3. Що таке логарифмічно-нормальний закон розподілу? Коли він застосовується?
4. Що таке математичне очікування, дисперсія та середньоквадратичне відхилення? Як вони визначаються?
5. Що таке критерій узгодженості і навіщо він потрібен?
6. Як визначається «критерій χ2» та за якої умови гіпотеза вважається достовірною?