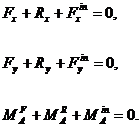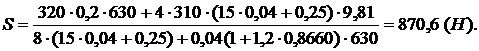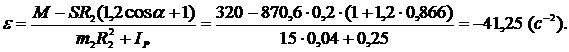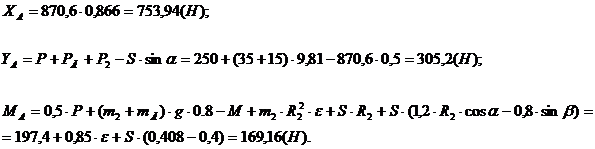|
|
||
|
|
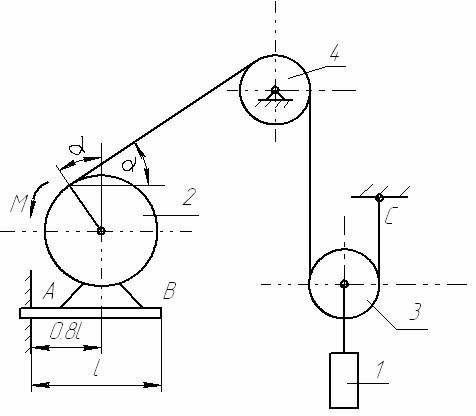
2.2 Приклад виконання завдання 2.1 Приклад виконання завдання Вантаж 1 (рис. 2.6) тросом з'єднаний з центром мас рухомого блока 3, який приводиться до руху пасом, один кінець якого закріплений в точці С, а другий перекинутий через нерухомий блок 4 і зафіксований на барабані 2 масою m2, що приводиться до руху електродвигуном з моментом М. Знайти реакції жорсткого защемлення А однорідної балки АВ довжиною 1 і вагою Р. Масою блока 4, троса та паса знехтувати. Маса електродвигуна mд , момент інерції ротора - Ір . Тіло 3 - однорідний диск, а маса барабана 2 розподілена по ободу радіуса R2. Дані для розрахунку: m1 = 300 кг; Ір= 0,25 кг×м2; m3= 10 кг; m2= 15 кг; mд = 35 кг; Р = 250 Н; 1 = 1м; R2= 0,2 м; М = 320 Н×м; α= 30°.
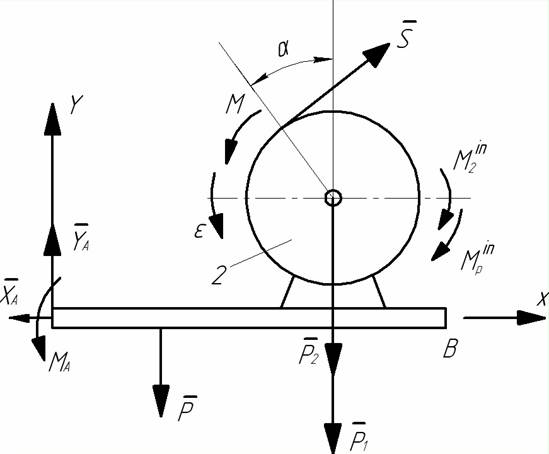
Рисунок АМ2.6 Розв'язування. Розглянемо матеріальну систему, що складається з балки АВ, електродвигуна і барабана 2 (рис. 2.7).
Рисунок АМ2.7
Запишемо принцип
Д'Аламбера для плоскої довільної системи сил в проекціях на осі
Рівняння рівноваги (2.1) для механічної системи (рис. АМ2.7) записуються у вигляді:
де S - реакція паса,
В трьох рівняннях (2.2)
п'ять невідомих :
Рисунок АМ2.8 Рисунок АМ2.9
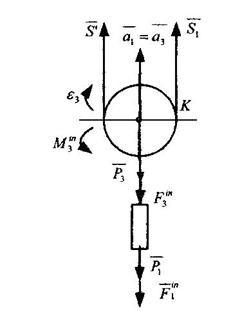
Рівняння рівноваги блока 3:
де
З врахуванням значень складових формули (2.3), маємо:
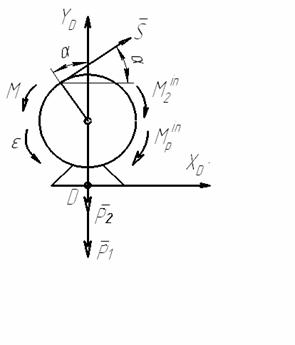
Рівняння рівноваги електромотора (рис. АМ2.9):
де xD, yD
– реакції в’язі балки АВ в точці D,
Після елементарних перетворень рівняння (2.5) має вигляд:
Із рівнянь (2.4) і (2.6) визначаємо натяг S паса:
Або, підставляючи дані умови задачі, отримаємо:
Враховуючи значення S, з рівняння (2.6) знаходимо кутове прискорення ротора електродвигуна та барабана:
Величину сил
|
|