Економіка підприємства
Практикум

Практична робота № 11
Тема. Оптимізація роботи підприємства на основі однофакторних економетричних моделей


Мета заняття: закріпити у студентів теоретичні знання та розвинути практичні навички щодо оптимізації роботи підприємства на основі однофакторних економетричних моделей.

Теоретичні відомості

Досить часто в практиці економічних досліджень намагаються визначити криву (поверхню), яка дає найкраще (в сенсі методу найменших квадратів) наближення вихідних даних. Відповідні методи наближення одержали назву регресійного аналізу.
Методи і моделі регресійного аналізу займають центральне місце в математичному апараті економетрії. Задачами регресійного аналізу є з’ясування форми залежності між змінними, оцінювання функції регресії, оцінювання невідомих значень (прогноз значень) залежної змінної.
У природничих науках часто йде мова про функціональну залежність, коли кожному значенню однієї змінної відповідає певне значення іншої (наприклад, швидкість вільного падіння у вакуумі в залежності від часу і т. п.).
Важливе місце в економетричних дослідженнях займає кореляційна залежність, при якій кожному значенню однієї змінної відповідає умовне середнє (умовне математичне сподівання) значення іншої.
Умовною середньою величиною називається середнє ариф¬метич-не значення ознаки Y, обчислене для конкретного значення показника Х.
Рівняння вигляду:
називається рівнянням регресії. При цьому ƒ(x) називається регресією Y на X, а графік цієї функції – лінією регресії. Залежну змінну Y називають також результативною ознакою, результативною функцією, ендогенною змінною, а незалежну змінну X – факторною ознакою, фактором, пояснювальною, екзогенною змінною та ін.
Іноді кореляційну залежність можна подати у вигляді модельного рівняння регресії:
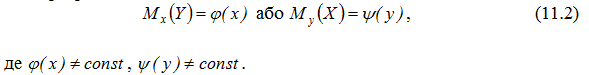
Розглянемо припущення, які є основою класичного кореляційно-регресійного аналізу (згідно з методом найменших квадратів).
1. Вектор помилок εi будемо називати збуренням.
2. Математичне сподівання збурення дорівнює нулю:
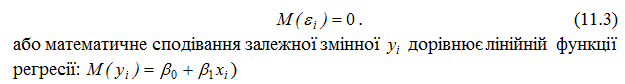
3. Дисперсія збурення εi (або залежної змінної yi) є сталою для довільного :
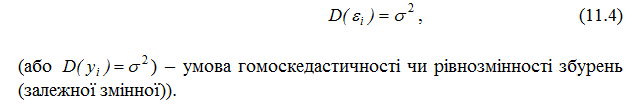
4. Збурення εi та εj некорельовані:
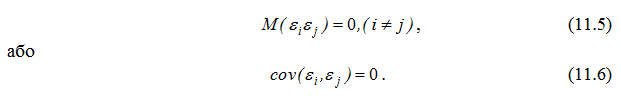
5. Незалежність між значеннями випадкової величини ε і значеннями незалежної змінної x:
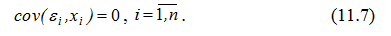
6. Випадкова величина εi розподілена за нормальним законом з математич¬ним сподіванням, рівним нулю, та дисперсією σ2.
7. Якщо параметри вибіркової лінійної кореляційно-регресійної моделі розраховані методом найменших квадратів за зроблених вище припущень, то
8. Регресійну модель специфіковано правильно (вибрано правильну функціональну форму моделі).
Економетричне дослідження містить етап специфікації моделі, що має бути адекватною економічному об’єкту, процесу, явищу, що вивчається. При специфікації моделі потрібно з’ясувати такі запитання:
1) які змінні потрібно вносити в модель;
2) якою повинна бути функціональна форма моделі: лінійною чи нелінійною, якщо нелінійною, то якою: степеневою, показниковою тощо;
3) які можливі припущення щодо змінних x, y, ε можна зробити в моделі?
На етапі специфікації економетричної моделі потрібно залучати експертів або проводити послідовні економетричні дослідження для вдосконалення моделі. Прості лінійні регресійні моделі встановлюють залежність між двома змінними: факторною і результативною ознаками. Наприклад, між витратами на відпустку і складом сім'ї, між витратами на рекламу і обсягом реалізованої продукції.
У загальному вигляді проста вибіркова лінійна регресія записується так:
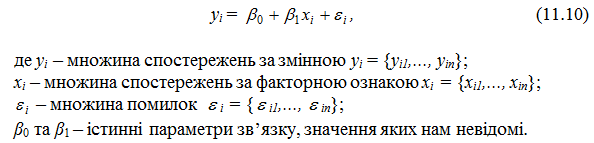
Регресійна модель називається лінійною, якщо вона лінійна за своїми параметрами. Модель (11.10) називають узагальненою парною лінійною кореляційно-регресійною моделлю.
Параметр β1 називають коефіцієнтом регресії, параметр β0 називають вільним членом кореляційно-регресійної моделі. Випадкова величина ε містить різноманітні стохастичні збурення, помилки спостереження та вимірювання, елементи випадковості людської реакції тощо.
Наше завдання – на основі заданих статистичних значень змінних x та отримати оцінки b0 та b1 параметрів β0 та β1 (в сенсі певного критерію), тобто побудувати рівняння регресії
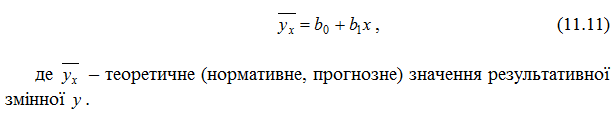
Приклад 1. Бюро економічного аналізу фабрики “ROSHEN” оцінює ефективність відділу маркетингу з продажу цукерок і тістечок. Для такого оцінювання є досвід праці у 5 географічних зонах з майже однаковими умовами (потенційні клієнти, ставлення до товарного знака і т. п.). У цих зонах зафіксовано протягом однакового періоду обсяги продажу (млн коробок), витрати (млн грн) фірми на просування товару на ринку. Вихідні дані наведено в табл. 11.1.
Реальні спостереження yi зобразимо точками у системі координат (X, Y) на рис. 11.1. Візуально можна припустити, що між даними є лінійна залежність, тобто їх можна апроксимувати прямою лінією.
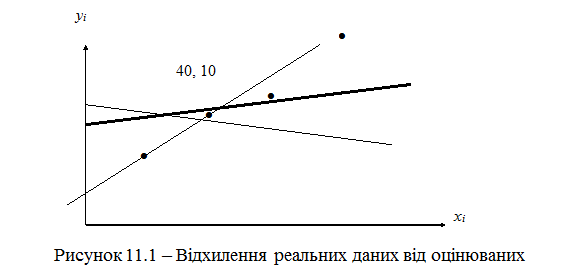
Взагалі існує безліч прямих, які можна провести через множину спостережуваних точок. Для цього треба скористатися критерієм, який дасть змогу вибрати «найкращу» з них, з точки зору цього критерію. Найпоширенішим є критерій мінімізації суми квадратів відхилень.
На рисунку будь-яка з прямих, яку можна провести через дані точки, має точки, які знаходяться над прямою і під нею. Встановимо відхилення від безпомилкової прямої так:
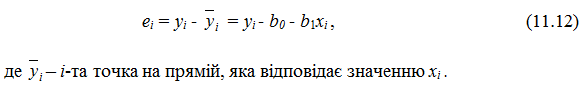
Відхилення або помилки називають ще залишками. Зрозуміло, що логічно вибирати таку пряму, щоб сума квадратів помилок була мінімальною.
У цьому полягає критерій найменших квадратів: невідомі параметри b0 та b1 визначаються таким чином, щоб мінімізувати суму квадратів помилок:
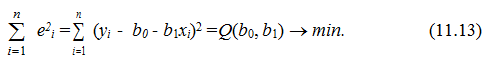
Дослідимо функцію Q(b0, b1) на мінімум. Необхідною умовою екстремуму є:
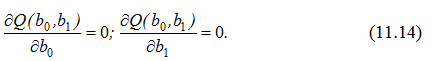
У нашому випадку маємо:
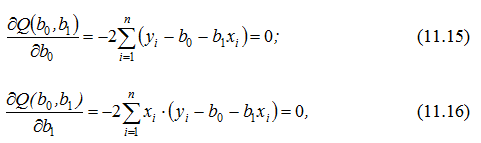
звідки отримаємо систему лінійних рівнянь:
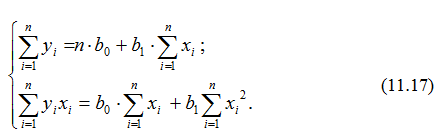
Систему (11.17) називають системою нормальних рівнянь для знаходження оцінених коефіцієнтів рівняння регресії.
Виразимо b0 з першого рівняння і підставимо у друге, отримаємо b1:
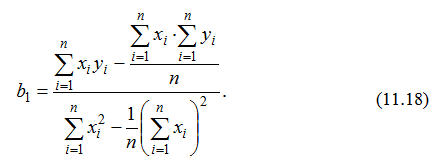
З метою спрощення помножимо чисельник і знаменник на 1/n:
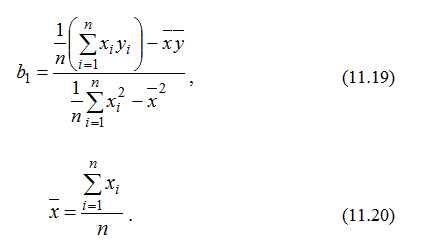
Вираз (11.18) можна записати ще так:
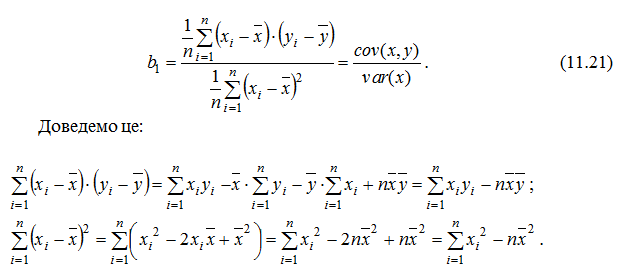
Чисельник (11.21) є коефіцієнтом коваріації між x та y. За визначенням, коефіцієнт коваріації визначається за формулою:
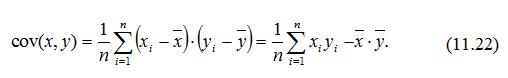
Коваріація (cov) – це абсолютна міра зв’язку між двома величинами.
Знаменник (11.22) є дисперсією величини x, тобто:
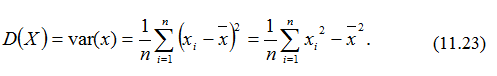
Отже, кут нахилу прямої регресії можна встановити за формулами (11.19) чи (11.21). Із першого рівняння системи (11.18) знайдемо параметр bо:
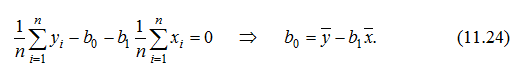
Таким чином, точка (b0, b1) є точкою, “підозрілою” на екстремум. Перевіримо, що дана точка є точкою мінімуму. Достатньою умовою мінімуму функції Q (b0, b1) є:
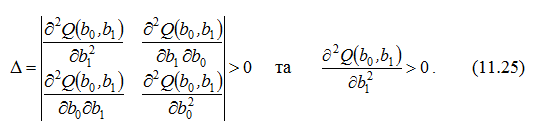
У нашому випадку маємо:
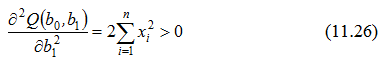
для неперервних функцій:
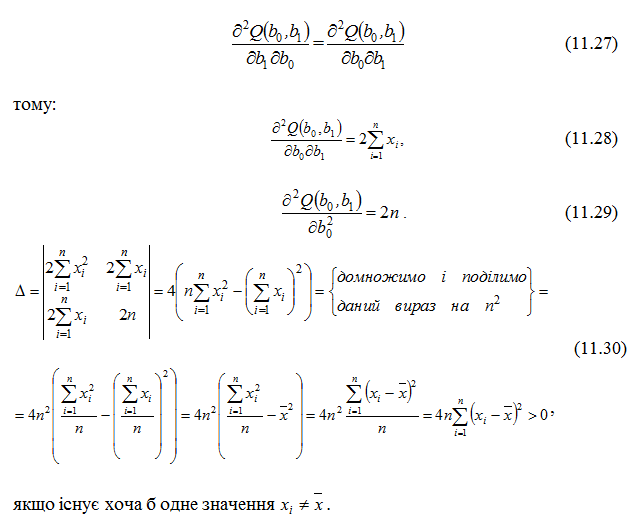
Приклад 2. Припустимо, що ви збираєте дані про витрати родини на відпустку та її доходи і оцінюєте це таким рівнянням:
Визначити, що є залежною змінною, а що − незалежною? Поясніть взаємозв’язок між витратами на відпустку родини і її доходом. Наскільки зростуть витрати, якщо дохід зросте на одиницю?
Розв’язання. Оскільки витрати на відпустку залежать від доходу родини, то витрати є залежною, а дохід – незалежною змінною.
Дане рівняння свідчить про те, що витрати складаються з двох частин. Перша частина подана перетином b0=5, що означає, розмір витрат y = 5 при відсутності доходу. Друга частина складається з 0,86x, тобто зростання доходу на одну одиницю зумовить зростання витрат на відпустку на 0,86.
Приклад 3. На підставі даних про валовий регіональний продукт та величину основних засобів по регіонах центру України за 2011 рік (табл. 3.2) побудувати лінійну кореляційно-регресійну модель, яка описує залежність величини валового регіонального продукту від величини основних засобів.
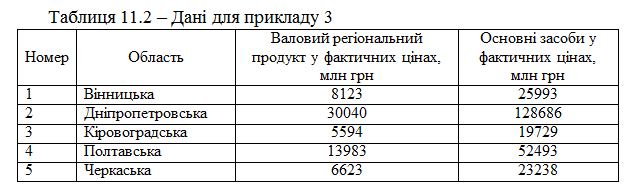
Розв’язання. Для побудови системи нормальних рівнянь (11.10) доцільно скласти допоміжну таблицю (табл. 11.3).
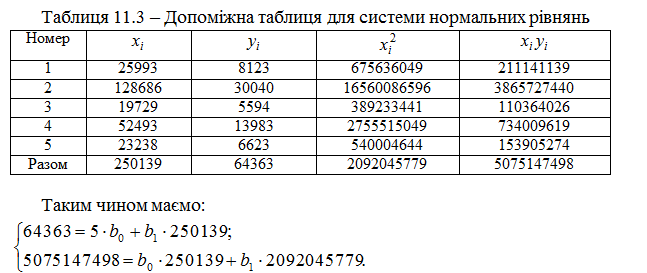
Розв’язавши одержану систему методом Крамера, знаходимо:
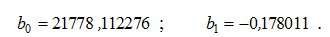
Отже, лінійна кореляційно-регресійна модель, яка описує залежність величини валового регіонального продукту від величини основних засобів, така:
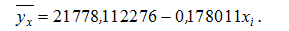
Щільність зв’язку між ознаками оцінюють за допомогою коефіцієнта кореляції, який обчислюється за формулою:
На практиці досить часто для обчислення коефіцієнта кореляції використовують і такі підходи:
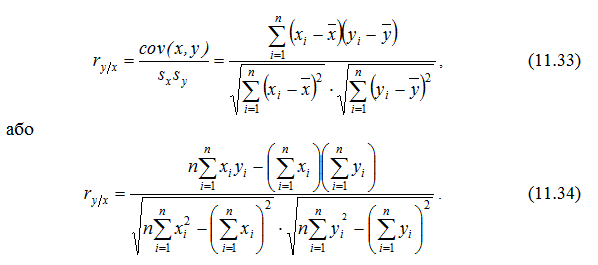
Властивості коефіцієнта кореляції.
1. Якщо ry/x >0, то кореляційний зв’язок прямий, при якому збільшення однієї змінної приводить до збільшення іншої змінної.
2. Якщо ry/x < 0, то кореляційний зв’язок зворотний, при якому збільшення однієї величини приводить до зменшення іншої.
3. Якщо = 1, то кореляційна залежність лінійна, тобто всі емпіричні точки лежать на прямій.
4. ry/x ∈ [-1,1].
5. Якщо =0, то лінійний зв’язок відсутній і лінія регресії паралельна осі Ох.
Кореляційний зв’язок між ознаками може бути слабким і сильним (щільним). Він оцінюється за шкалою Чеддока таким чином:
0,1 < ry/x < 0,3: слабкий;
0,3 < ry/x < 0,5: помірний;
0,5 < ry/x < 0,7: помітний;
0,7 < ry/x < 0,9: щільний;
0,9 < ry/x < 1: дуже щільний.
Приклад 4. За даними прикладу 3 оцінити силу кореляційного зв’язку між величиною валового регіонального продукту та величиною основних засобів.
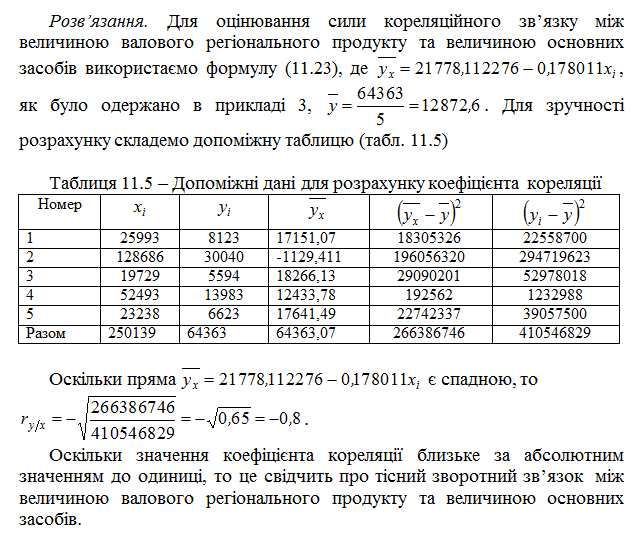
Приклад 5. Знайти рівняння регресії залежності між видобутком вугілля на одного шахтаря за зміну та потужністю пласту за такими даними, що характеризують процес видобутку вугілля на 10 шахтах (таблиця 11.6).
Обчислити коефіцієнт кореляції.
Розв’язання. Для знаходження рівняння регресії складемо систему нормальних рівнянь за допомогою допоміжної таблиці (табл. 11.7).
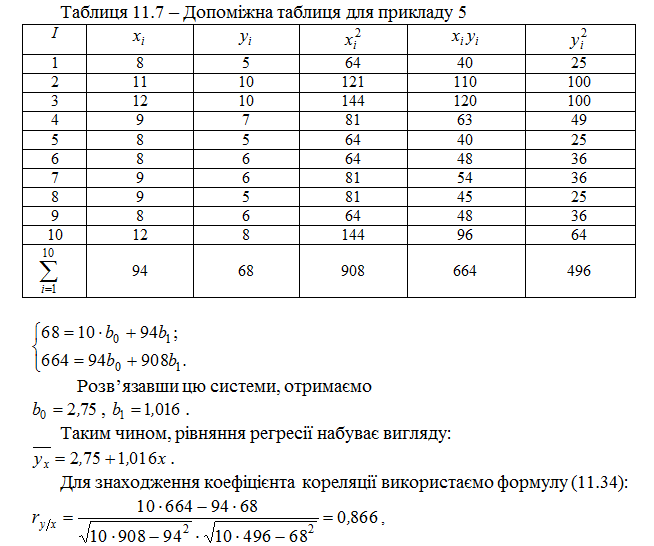
тобто, зв’язок між змінними досить тісний.
Одним із важливих питань кореляційного аналізу є перевірка значи-мості рівняння регресії, тобто встановлення адекватності математичної моделі експериментальним даним (реальному об’єкту). Однією з найбільш ефективних оцінок адекватності регресійної моделі є коефіцієнт детер¬мі¬нації, який обчислюється за формулою:
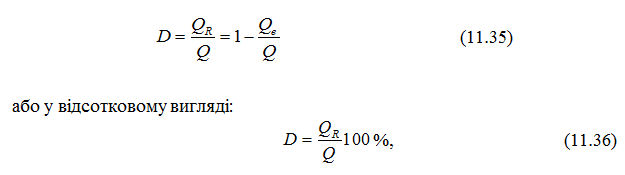
і показує, яка частина варіації змінної Y залежить від змінної X, а яка − від неврахованих факторів. Рівняння регресії буде адекватне експери¬мен-тальним даним, якщо D ∈ [0,55; 1].
Відмітимо, що коефіцієнт детермінації є сенс розглядати лише за наявності вільного члена в рівнянні регресії, оскільки лише в цьому випадку рівність (11.21) є правильною. Якщо є відомим коефіцієнт детермінації, то критерій значимості рівняння регресії або самого коефіцієнта детермінації можна записати так:
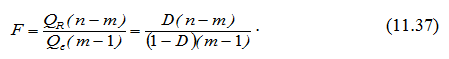
У випадку парної лінійної регресії коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції. Дійсно:
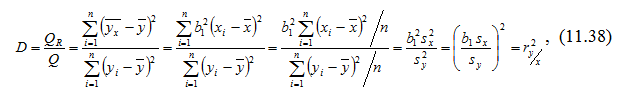
Приклад 6. За даними прикладу 5 знайти коефіцієнт детермінації та пояснити його зміст.
За таблицею F-розподілу (дод. Д) F0,05;1,8 = 4,20. Оскільки розраховане значення більше за табличне, то з ймовірністю помилитися не більше ніж у 5% випадків можна стверджувати, що рівняння регресії є значущим.

Завдання для самостійного виконання

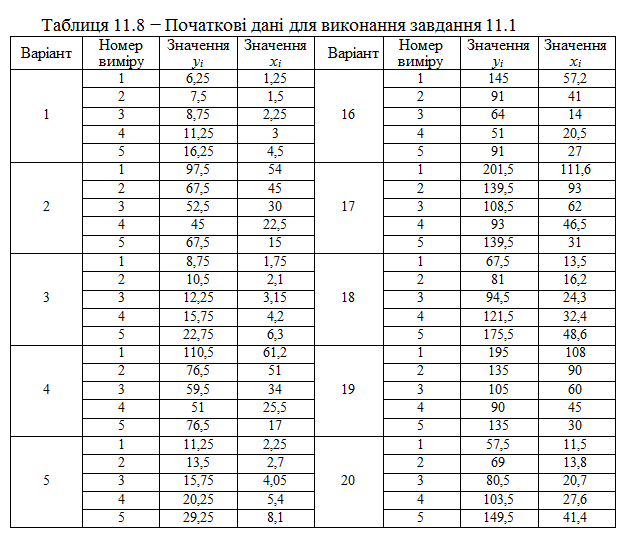
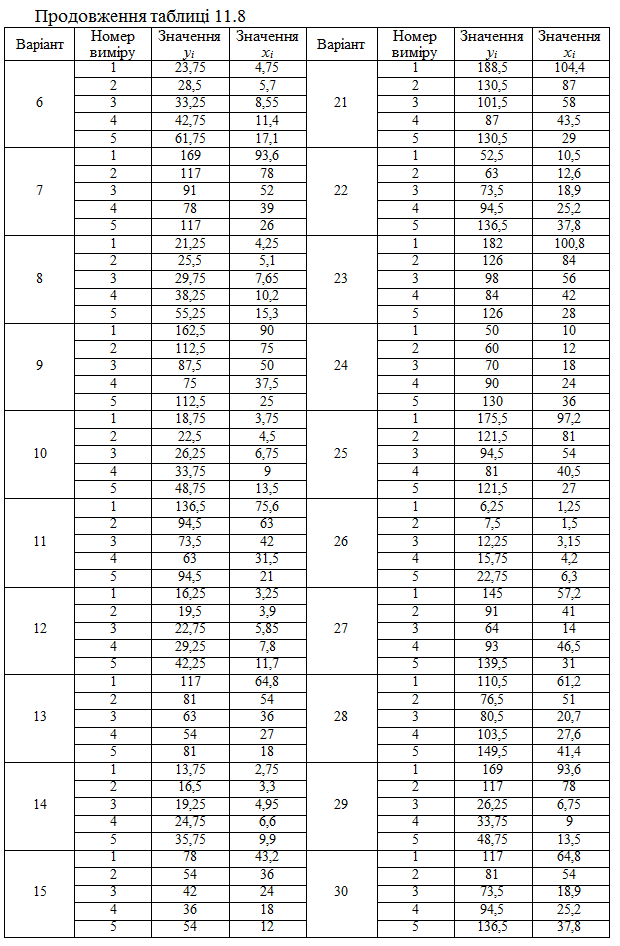
Керуючись даними таблиці 11.8, потрібно

1. Побудувати економетричну модель залежності y від фактора x.
2. Оцінити щільність зв’язку між змінними та адекватність побудованої моделі.
3. Зробити висновки.

Питання для самоконтролю

Який зв’язок між економічними показниками називають балансовим?
2. Що називають умовною середньою величиною?
3. Яку залежність називають кореляційною? Наведіть приклади.
4. Що таке рівняння та лінія регресії?
5. Запишіть загальний вигляд простої лінійної вибіркової регресії.
6. За яким критерієм оцінюють параметри лінійного рівняння регресії?
7. Охарактеризуйте метод найменших квадратів для оцінювання параметрів лінійної регресії та виведіть відповідну систему нормальних рівнянь.
8. Запишіть формулу для обчислення коефіцієнта коваріації.
9. Сформулюйте основні припущення кореляційного аналізу.
10. Опишіть F-критерій Фішера-Снедекора.
11. Що характеризує коефіцієнт кореляції і як його можна обчислити?

Тестові завдання