Практична робота № 12
Тема. Оптимізація роботи підприємства на основі однофакторного
кореляційного аналізу
Мета заняття: закріпити у студентів теоретичні знання та розвинути практичні навички щодо оптимізації роботи підприємства на основі однофакторного кореляційного аналізу.
Теоретичні відомості
Нелінійна кореляційна залежність. Пошук рівняння регресії – одна з найважливіших проблем кореля¬ційного аналізу. На практиці в економічних дослідженнях іноді потрібно розглядати нелінійні рівняння регресії.
Як і у випадку лінійної регресії для знаходження оцінок параметрів рівнянь регресії потрібно розв’язати відповідні системи нормальних рів-нянь. Наведемо деякі типи нелінійних кореляційних рівнянь та відпо¬від-них їм систем нормальних рівнянь, де для спрощення запису замість 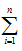 записано Σ.
записано Σ.
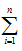 записано Σ.
записано Σ.
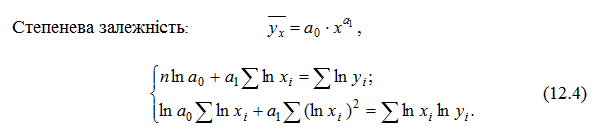
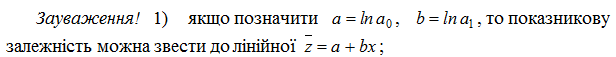
2) щільність показників також оцінюють за допомогою коефіцієнта кореляції (див. форм. (11.32));
3) адекватність нелінійної моделі встановлюють за допомогою коефіцієнта детермінації (див. форм. (11.35) або (11.36)).
До нелінійних моделей наводять дослідження динаміки поведінки економічних систем. П. Самуельсон та В. Фріск визначають динамічну систему так: “…систему називають динамічною, якщо її поведінка в часі визначена функціональними рівняннями, в яких змінні в різні моменти часу присутні в явному вигляді”. Такі дослідження дають можливість визначити перспективи розвитку цих систем, виявити можливі резерви, розробити комплекс адаптивних управлінських рішень, які забезпечать ефективне функціонування економічних об’єктів. Дослідженням детермінованої поведінки економічних систем в часі та визначенням оптимальної траєкторії їх розвитку займається економічна динаміка. Трендові, лагові та факторні моделі економічної динаміки є економетричними моделями.
Алгоритм розв’язання практичної задачі однофакторного кореляційного аналізу. Нехай для виробничого підприємства відомі такі показники: кількість виробленого та реалізованого продукту К (тис. одиниць), ціна Ц (тис. грошових од. за одиницю продукції), витрати В виробництва за повною собівартістю (млн грошових од.). Необхідно провести аналіз на оптимальність обсягу реалізації продукції за критерієм максимального прибутку та розробити стратегію підприємства на майбутні періоди.
Відомо, що прибуток підприємства обчислюється за формулою:

Зрозуміло, що в даному випадку ціна та витрати виробництва за повною собівартістю, а отже і прибуток, кореляційно залежать від кількості виробленого та реалізованого продукту. Тому в наших розрахунках ми будемо одержувати функцію прибутку, аналітичний вираз якої в спрощеному вигляді можна записати так:

При розв’язуванні даної практичної задачі потрібно дотримуватися певного алгоритму.
1. Знаходимо аналітичні рівняння регресії для ціни та витрат: ЦK=Ц(К), BK =В(К).
Для виконання цього пункту потрібно спочатку нанести на координатні площини КОЦ та КОВ емпіричні дискретні точки та зробити припущення щодо форми відповідної лінії регресії. За допомогою нормальних систем оцінюємо значення парамет¬рів вибраних рівнянь регресії.
2. Перевіряємо адекватність знайдених рівнянь регресії. Оцінюємо щільність зв’язку між кількістю виробленого та реалізованого продукту і ціною та кількістю і витратами.
Адекватність знайдених рівнянь регресії перевіряємо за допомогою коефіцієнта детермінації, який обчислюємо за формулою (11.35) або за (11.36). Варто нагадати, що рівняння будуть значущими, якщо коефіцієнт детермінації D належить відрізку [0,55; 1]. Якщо D ∈ [0,45; 0,55], то для встановлення адекватності моделі реальному об’єкту використовують F-критерій Фішера.
За умови, що 0 < D < 0.45, знайдене рівняння регресії неадекватне, наше припущення щодо форми лінії регресії недостовірне і потрібно робити інше припущення.
Оцінити щільність зв’язку між відповідними показниками та зробити необхідні висновки можна за допомогою коефіцієнта кореляції ( rЦ/K та rB/K ), який обчислюється за однією з формул (11.32) − (11.34).
Зауваження! Неадекватність одержаних рівнянь регресії може бути пов’язана з використанням нераціональних методів розв’язування систем нормальних рівнянь або неточних заокруглень. Для усунення останнього недоліку пропонується в розрахунках використовувати числа не менше як із п’ятьма знаками після коми.
3. Будуємо функцію прибутку та знаходимо кількість виробленого і реалізованого продукту, при якій прибуток буде максимальним.
Для побудови функції прибутку підставляємо знайдені рівняння регресії для ціни та витрат у рівність (11.59). Одержану функцію прибутку досліджуємо на екстремум (знаходимо точку максимуму К0).
4. Робимо висновки, за даним критерієм, про стан підприємства та розробляємо стратегію на майбутні періоди.
Для одержання висновків щодо стану підприємства складається допоміжна порівняльна таблиця (табл. 12.1). Значення Кn, Цn, та Вn – статистичні дані динамічного ряду за останній період. Оптимальне значення кількості виробленого та реалізованого про¬дукту – це точка максимуму функції прибутку К0. Підставивши це зна¬чення в рівняння регресії ЦK=Ц(К), BK =В(К), отримаємо оптимальні ціну та витрати.
Аналізуємо значення відхилення фактичного значення показника від оптимального, робимо відповідні висновки та розробляємо стратегію підприємства на майбутні періоди.

Зауваження! Якщо в п.1 ми встановили, що крива прибутку має точку мінімуму, а не максимуму, то ми не зможемо розв’язати задачу за критерієм максимального прибутку. Ми можемо лише визначити мінімальний обсяг виробництва та мінімальні ціну й витрати.
Приклад 1. Для виробничого підприємства відомі такі показники за 6 періодів: кількість виробленого та реалізованого продукту К (тис. одиниць), ціна Ц (тис. грошових од. за одиницю продукції), витрати В виробництва за повною собівартістю (млн грош. од.) (табл. 12.2). Необхідно:
1) знайти кореляційну залежність ціни Ц та витрат В від кількості виробленого та реалізованого продукту К: Ц=Ц(К), B=В(К).
2) оцінити щільність зв’язку між відповідними ознаками за кореля-ційним відношенням, обчислити коефіцієнт детермінації;
3) провести аналіз на оптимальність обсягу реалізації продукції за критерієм максимального прибутку;
4) зробити висновки та розробити стратегію підприємства на майбутні періоди.
1) знайти кореляційну залежність ціни Ц та витрат В від кількості виробленого та реалізованого продукту К: Ц=Ц(К), B=В(К).
2) оцінити щільність зв’язку між відповідними ознаками за кореля-ційним відношенням, обчислити коефіцієнт детермінації;
3) провести аналіз на оптимальність обсягу реалізації продукції за критерієм максимального прибутку;
4) зробити висновки та розробити стратегію підприємства на майбутні періоди.

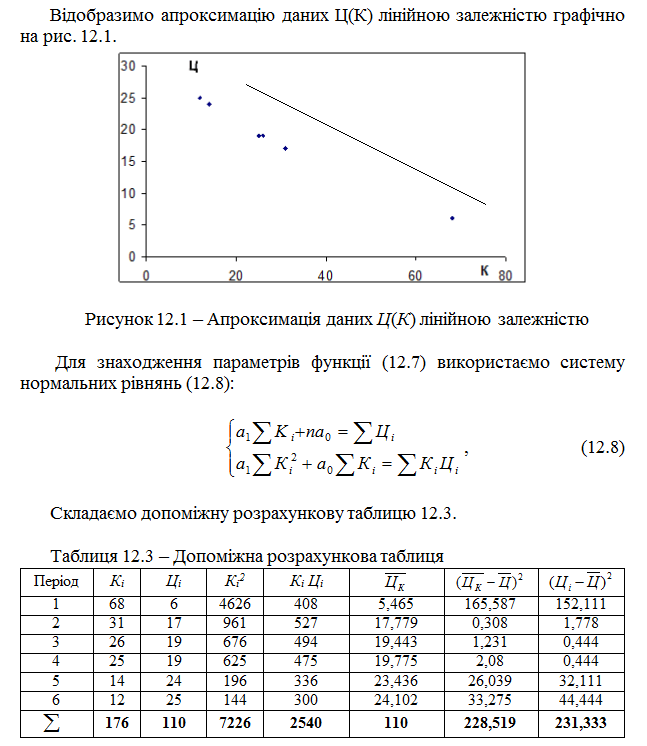

Підставляючи по черзі значення Кі в рівняння (12.9), отримаємо відповідні значення ЦK, якими заповнюємо шосту графу таблиці 12.3, а за цими значеннями та значеннями Цi і Ц обчислюємо елементи сьомої та восьмої граф цієї таблиці.
Щільність зв’язку між ознаками Ц та К обчислюємо за допомогою коефіцієнта кореляції:
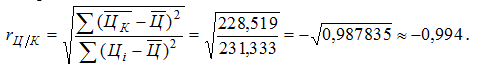
Знак «–» для попередніх розрахунків вибираємо з тієї причини, що пряма (12.1) є спадною.
Оскільки значення коефіцієнта кореляції близьке за абсолютним значенням до одиниці, то це свідчить про щільний зворотний зв’язок між ціною товару та його реалізованою кількістю. Коефіцієнт детермінації D є підкореневим виразом останньої формули. Цей коефіцієнт показує, що варіація результативної ознаки (ціни товару) на 98% відбувається під впливом фактора кількості реалізованого продукту, а на 2% – під впливом неврахованих в моделі факторів.
Визначимо тип залежності В(К) за допомогою графіка, що апроксимує дані кореляційної таблиці до функції, зображеної на рис. 12.2.
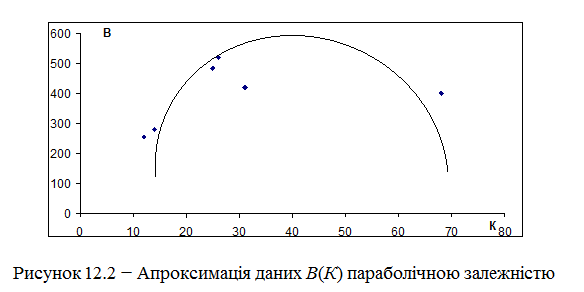
Із рисунка 12.2 можна припустити, що залежність між витратами та кількістю виробленої та реалізованої продукції має квадратичний характер:

Для пошуку параметрів параболічної залежності скористаємося системою нормальних рівнянь (12.11):
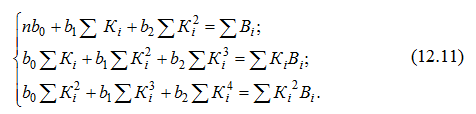
Для розрахунку значень параметрів параболічної однофакторної моделі необхідно скласти відповідну допоміжну таблицю 12.4.
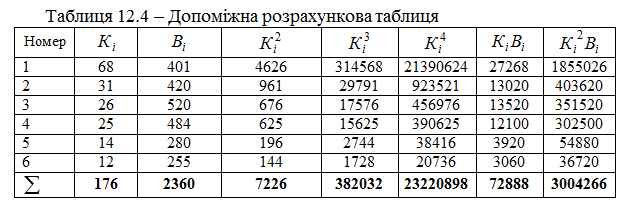
Таким чином, система нормальних рівнянь набуває вигляду:
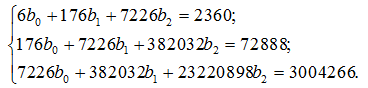
Розв’язавши систему засобами Mathcad, знаходимо:
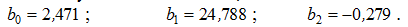
Тому шукане рівняння регресії таке:

Щільність зв’язку між ознаками В та К обчислюємо за допомогою коефіцієнта кореляції так:
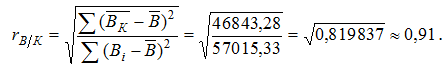
Оскільки значення коефіцієнта кореляції близьке до одиниці, то це свідчить про щільний прямий зв’язок між витратами на виробництво та кількістю реалізованої продукції. Коефіцієнт показує, що варіація результативної ознаки (витрат) на 91% відбувається під впливом фактора кількості реалізованого продукту, а на 9% − під впливом неврахованих в моделі факторів. Отже, побудоване рівняння регресії є адекватним реальному об’єкту.
Використовуючи рівняння (12.9) та (12.12), знаходимо формулу прибутку від реалізації продукту:
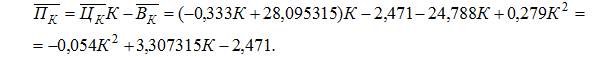
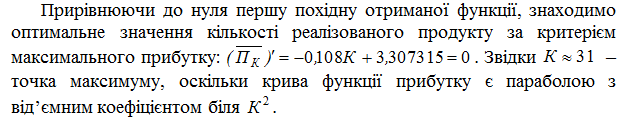
Таким чином, оптимальний обсяг випуску та реалізації продукту складає 31 одиницю. За цією величиною можна обчислити оптимальну ціну продукту, за рівнянням (12.9), оптимальні витрати, за рівнянням (12.12), виручку від реалізації та оптимальний прибуток. Результати розрахунків подано в таблиці 12.6.
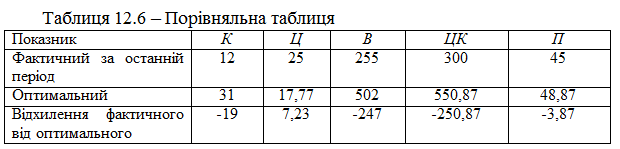
Висновки:
1) лінійна залежність Ц=Ц(K) та квадратична B=B(K) є гарними наближеннями для вихідних даних, що засвідчується отриманими значеннями коефіцієнтів кореляції. Такий результат дозволяє прогнозувати значення кількості виробленого та реалізованого продукту при наявності значень щодо ціни одиниці продукції або витрат на цей обсяг продукції за повною собівартістю. І навпаки, маючи заплановану оптимальну кількість виготовленого продукту можна визначити, виходячи з оцінених рівнянь, оптимальну ціну, яку необхідно встановити, та витрати, що може собі дозволити виробник;
2) прибуток підприємства на 3,87 млн грош. од. менший оптимального за рахунок недовиробництва;
3) кількість виробленої та реалізованої продукції менша за оптимальну на 19 тис. одиниць за рахунок перевищення ціни на 7,23 тис. грош. од.;
4) стратегія підприємства: зростання обсягу випуску та реалізації продукту, зменшення ціни.
Завдання для самостійного виконання
Для виробничого підприємства за шість періодів відомі кількість виробленого та реалізованого продукту, ціна за одиницю продукції, витрати виробництва за повною собівартістю.
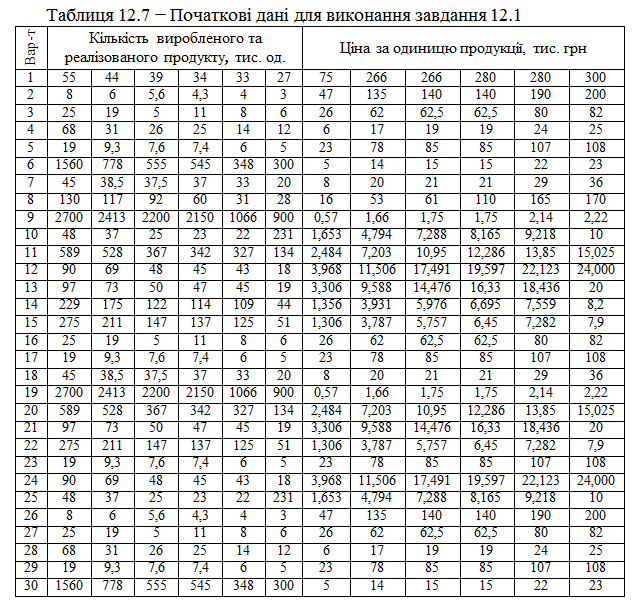
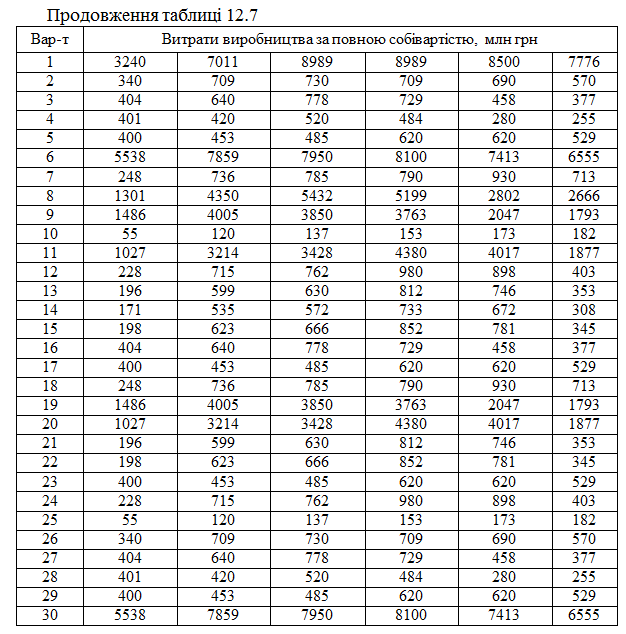
Керуючись даними таблиці 12.7, потрібно
1. Знайти кореляційну залежність ціни Ц та витрат В від кількості виробленого та реалізованого продукту К: ЦK =Ц(К), BK =В(К).
2. Оцінити щільність зв’язку між відповідними ознаками за кореляційним відношенням, обчислити коефіцієнт детермінації.
3. Відобразити графічно апроксимацію даних В(К) параболічною залежністю та апроксимацію даних Ц(К) лінійною залежністю.
4. Провести аналіз на оптимальність обсягу реалізації продукції за критерієм максимального прибутку.
5. Зробити висновки та розробити стратегію підприємства на майбутні періоди.
2. Оцінити щільність зв’язку між відповідними ознаками за кореляційним відношенням, обчислити коефіцієнт детермінації.
3. Відобразити графічно апроксимацію даних В(К) параболічною залежністю та апроксимацію даних Ц(К) лінійною залежністю.
4. Провести аналіз на оптимальність обсягу реалізації продукції за критерієм максимального прибутку.
5. Зробити висновки та розробити стратегію підприємства на майбутні періоди.
Питання для самоконтролю
1. Які дослідження приводять до нелінійних моделей? Наведіть приклади таких моделей.
2. Опишіть алгоритм розв’язання практичної задачі кореляційного аналізу.
3. Які дослідження приводять до нелінійних моделей? Наведіть приклади таких моделей.
4. Спробуйте вивести одну із систем нормальних рівнянь для оцінювання параметрів нелінійної кореляційної залежності.
5. Якою є система нормальних рівнянь для параболічної залежності?
6. Якою є система нормальних рівнянь для гіперболічної залежності?
7. Якою є система нормальних рівнянь для показникової залежності?
8. Якою є система нормальних рівнянь для степеневої залежності?
9. Якою є формула для параболічної залежності?
10. Якою є формула для гіперболічної залежності?
11. Якою є формула для показникової залежності?
12. Якою є формула для степеневої залежності?
2. Опишіть алгоритм розв’язання практичної задачі кореляційного аналізу.
3. Які дослідження приводять до нелінійних моделей? Наведіть приклади таких моделей.
4. Спробуйте вивести одну із систем нормальних рівнянь для оцінювання параметрів нелінійної кореляційної залежності.
5. Якою є система нормальних рівнянь для параболічної залежності?
6. Якою є система нормальних рівнянь для гіперболічної залежності?
7. Якою є система нормальних рівнянь для показникової залежності?
8. Якою є система нормальних рівнянь для степеневої залежності?
9. Якою є формула для параболічної залежності?
10. Якою є формула для гіперболічної залежності?
11. Якою є формула для показникової залежності?
12. Якою є формула для степеневої залежності?
Тестові завдання




