Практична робота № 13
Тема. Прогнозування основних показників роботи підприємства на основі багатофакторних економетричних моделей
Мета заняття: закріпити у студентів теоретичні знання та розвинути практичні навички щодо прогнозування основних показників роботи підприємства на основі багатофакторних економетричних моделей.
Теоретичні відомості
Економічні явища, як правило, визначаються великою кількістю факторів. Кожна економічна змінна залежить не від одного, а від багатьох факторів. Наприклад, валовий регіональний продукт залежить не лише від величини основних засобів, а й від величини оборотних фондів; величини інвестицій в основний капітал; кількості людей, зайнятих на підприєм¬ст¬вах регіону, технологій, які використовуються; ефектив¬ності управлін¬ських рішень тощо. Урожайність деяких культур залежить від родючості ґрунту, кількості внесених органічних і мінеральних добрив, сорту насіння, агротехнічного оброблення, природних умов тощо. Спільний вплив кількох факторів на одну результативну змінну досліджують за допомогою багатофакторних економетричних моделей.
Класична нормальна лінійна модель множинної регресії. При¬пус-тимо, що потрібно дослідити залежність змінної Y від змінних X1, X2,…, Xp. Позначимо і-те спостереження залежної змінної yi, пояснювальних
змінних − xi1, xi2,…, xip. Тоді модель множинної регресії така:
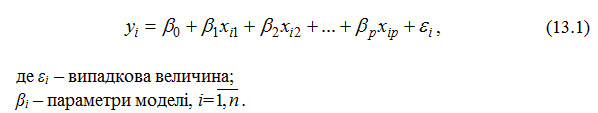
Модель (13.1) називають класичною нормальною лінійною моделлю множинної регресії. Залежна змінна Y називається також пояснюваною, ендогенною змінною, незалежні змінні Xі – пояснювальними, екзогенними змінними.
Введення більшої кількості пояснювальних змінних ускладнює математичне оброблення даної моделі, тому виникла доцільність використання матричних позначень:
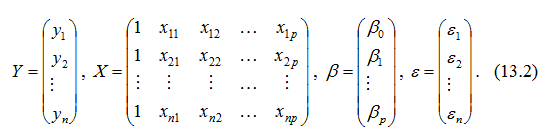
Звертаємо увагу на те, що до матриці X введено додатковий стовпець, усі елементи якого дорівнюють 1, тобто умовно припускаємо, що в моделі (13.1) вільний член β0 множиться на фіктивну змінну xi0, яка дорівнює 1 для всіх значень i.
Враховуючи позначення (13.2) модель (13.1) набуває вигляду:

Оцінкою моделі (4.1) за вибіркою є рівняння вигляду:
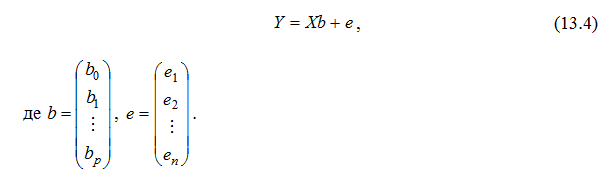
Оцінювання параметрів класичної регресійної моделі за методом найменших квадратів. За методом найменших квадратів параметр b вибирається таким, щоб сума квадратів відхилень була мінімальною, тобто:

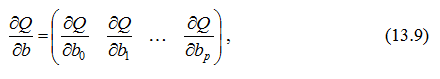
Для вектора частинних похідних можна довести такі твердження:

звідки одержуємо систему нормальних рівнянь в матричній формі для визначення вектора b:
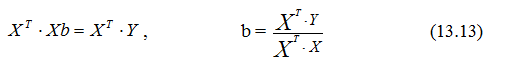
Згідно з цим методом параметр b знаходиться за формулою:
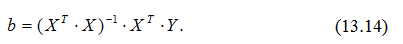
Тоді лінійна модель має вигляд:
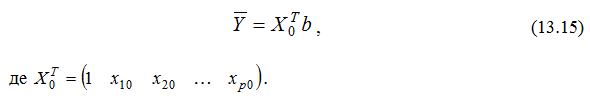

В окремому випадку, використовуючи матричне рівняння (13.13) з врахуванням (13.16) та (13.17) для однієї пояснювальної змінної, нескладно одержати відому систему нормальних рівнянь:
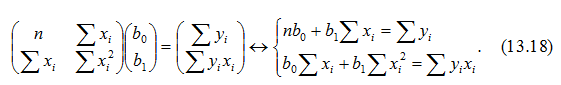
2) cистема (13.13) має розв’язок, якщо матриця XTX є невласною, тобто її визначник не дорівнює нулю.
Із другого зауваження можна одержати ще одну передумову множинного регресійного аналізу: вектори значень пояснювальних змінних або стовпці матриці X повинні бути лінійно незалежними.
Теорема Гаусcа – Маркова, розглянута для парної регресійної моделі, є справедливою і для моделі множинної регресії: за умови виконання передумов множинного регресійного аналізу оцінювання методом найменших квадратів b=(XTX)-1XTY є найбільш ефективним, тобто має дисперсію в класі лінійних несуміщених оцінок.
Приклад 1. Є такі дані (умовні) про видобуток вугілля за зміну на одного шахтаря Y (т), потужність пласту X1 (м) та рівні механізації робіт X2 (%), що характеризують видобуток вугілля на 10 шахтах (табл. 13.1)
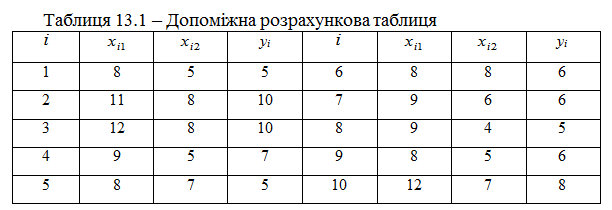
Припускаючи, що між змінними Y, X1, X2 існує лінійна кореляційна залежність, знайти її аналітичний вираз.
Розв’язання. Позначимо
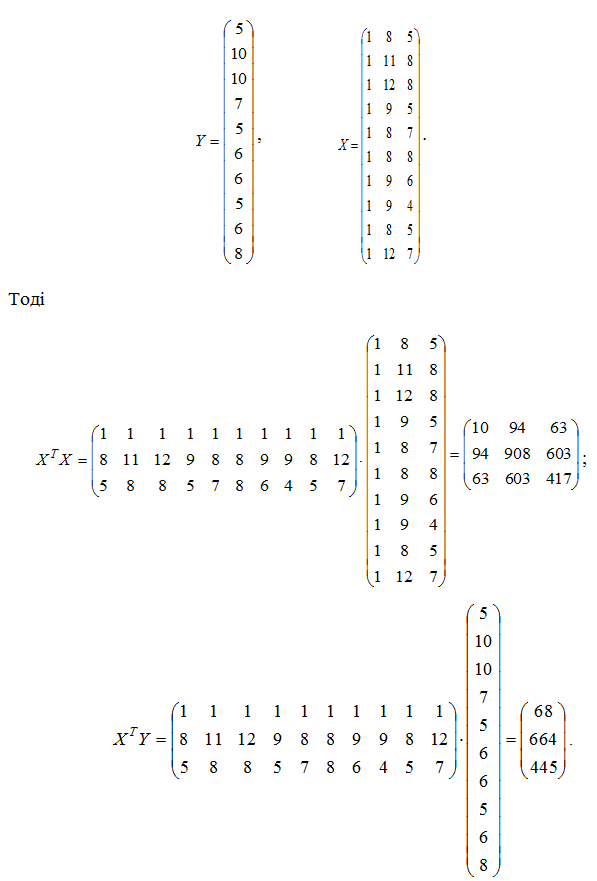
Знайдемо матрицю, обернену до XT X:

Одержане рівняння регресії показує, що при збільшенні потужності пласту X1 (за незмінного значення X2) лише на 1 м видобуток вугілля на одного шахтаря Y збільшується в середньому на 0,854 т, а при збільшенні рівня механізації робіт X2 (за незмінного значення X1) – в середньому на 0,367 т.

Коефіцієнт еластичності E j показує, на скільки відсотків зміниться в середньому Y, якщо xj збільшити на 1%.
Приклад 2. За даними прикладу 13.1 порівняти відокремлений вплив на видобуток вугілля за зміну двох факторів – потужності пласту та рівня механізації робіт.
Розв’язання. Оскільки
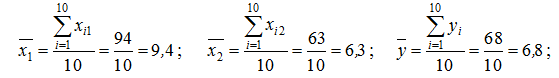
тому за формулами (13.19) коефіцієнти еластичності:
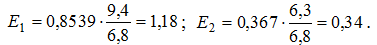
Таким чином, збільшення потужності пласту на 1% приводить до збільшення видобутку вугілля на 1,18%, а при збільшенні рівня механізації робіт на 1% видобуток вугілля збільшується на 0,34%. Останній результат показує, що на видобуток вугілля більший вплив має фактор “потужність пласту” у порівнянні з фактором “рівень механізації робіт”.
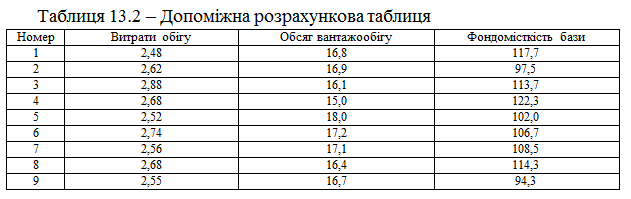
Приклад 3. Побудувати лінійну економетричну модель, що характеризує залежність між витратами обігу (Y), обсягом вантажообігу (X1) та фондомісткістю бази (X2). Визначити коефіцієнти еластичності. Вихідні дані наведені в таблиці 13.2.

Застосувавши засоби Mathcad знаходимо:
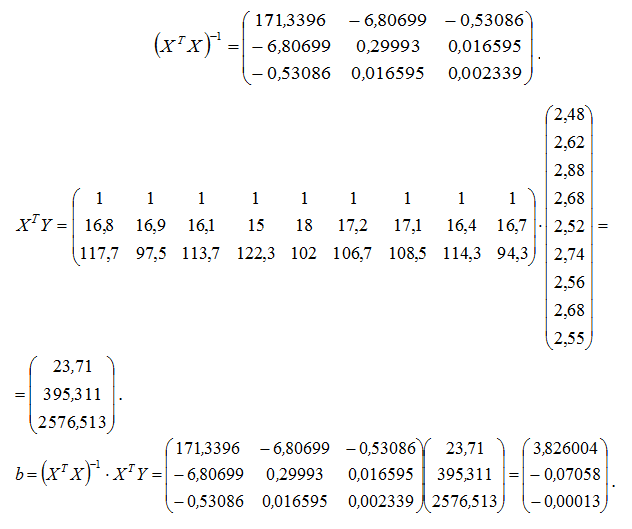
Із врахуванням рівності (13.15)
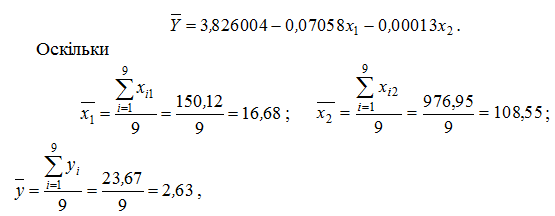
то за формулою (13.19) коефіцієнти еластичності:

Перевірка двофакторної регресії на адекватність за допомогою коефіцієнта детермінації критерію Фішера. Як і у випадку парної регресійної моделі сума квадратів відхилень залежної змінної від середнього може бути розвинена на дві складові:
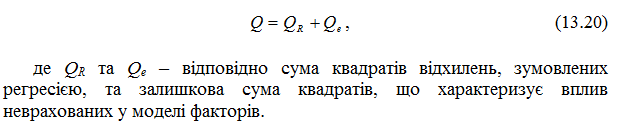
Знайдемо формули для пошуку відповідних сум квадратів.
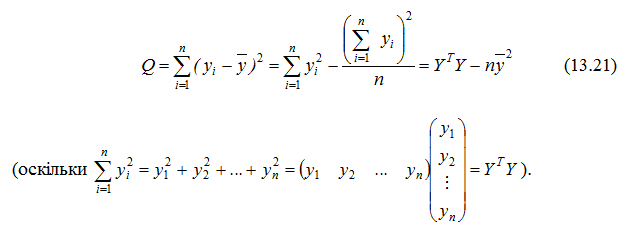
Із врахуванням (13.12) маємо
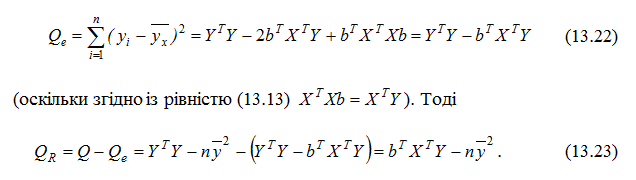
Рівняння множинної регресії є значущим (іншими словами – гіпотеза H0 про рівність нулю параметрів регресійної моделі відкидається).
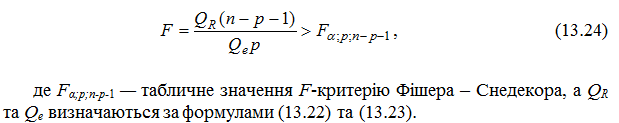
Коефіцієнт детермінації D є однією із найбільш ефективних оцінок адекватності регресійної моделі, міри якості рівняння регресії, характеристики його прогностичної сили.
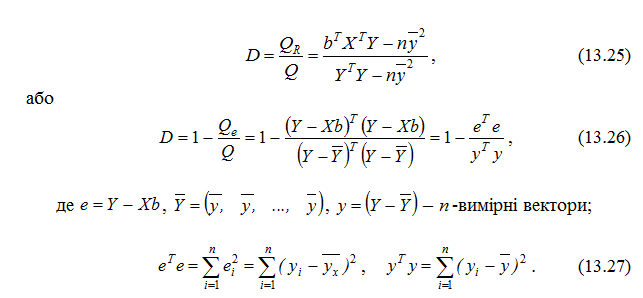
Нагадаємо, що коефіцієнт детермінації D характеризує частку варіації залежної змінної, зумовленої регресією. Чим ближчий цей коефіцієнт до одиниці, тим краще регресія описує залежність між пояснювальними та залежною змінними.
Разом із тим використання лише одного коефіцієнта детермінації для вибору найкращого рівняння регресії може виявитись недостатнім. На практиці зустрічаються випадки, коли неправильно визначена модель регресії може дати досить високий коефіцієнт детермінації.
Недоліком коефіцієнта детермінації є той факт, що він збільшується при додаванні нових пояснювальних змінних, хоча це не обов’язково означає покращення якості регресійної моделі. В цьому сенсі доцільніше використовувати скоригований (адаптований, виправлений) коефіцієнт детермінації , що визначається за формулою:
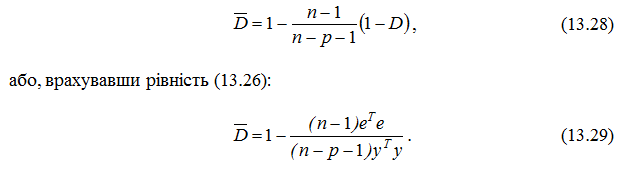
З рівності (13.28) випливає, що чим більше число пояснювальних змінних p, тим менший коефіцієнт D у порівнянні із D. Скоригований коефіцієнт детермінації D , на відміну від D, може зменшуватися при введенні в модель нових пояснювальних змінних, що не мають істотного впливу на залежну змінну. Однак навіть збільшення скоригованого коефіцієнта детермінації при введенні в модель нової пояснювальної змінної не завжди означає, що її коефіцієнт регресії є значущим (це відбувається лише в тому випадку, коли відповідне значення t-статистики більше за одиницю (за абсолютною величиною), тобто |t| > 1). Іншими словами, збільшення D ще не означає покращення якості регресійної моделі.
Якщо є відомим коефіцієнт детермінації D, то критерій значущості (13.24) рівняння регресії може бути записаний у вигляді (критерій Фішера):
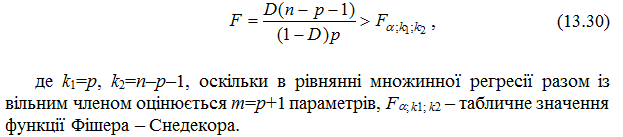
Приклад 4. За даними прикладу 1 визначити множинний коефіцієнт детермінації та перевірити значущість одержаного рівняння регресії Y за X1 та X2 на рівні a=0,05. Перевірити значущість рівняння регресії за критерієм Фішера.
Розв’язання. Обчислимо добутки векторів (див. приклад 1):

Такий коефіцієнт детермінації свідчить про те, що варіація дослід¬жу-ваної змінної Y – видобуток вугілля за зміну на одного робітника − на 81,1% залежить від потужності пласту X1 та рівня механізації робіт X2, 18,9% припадає на невраховані в моделі фактори. Отже, одержане в прикладі 4.1 рівняння регресії є значущим.
Перевіримо значущість рівняння регресії за критерієм Фішера. Фактичне значення критерію за (13.30):
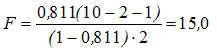
більше табличного F 0,5;2,7= 4,74 ; визначеного на рівні значимості α=0,05 при k1=2 та k2=10–2–1=7 ступенях вільності (див. дод. Е), тобто рівняння регресії є значущим і залежна змінна Y досить якісно описується внесеними в модель змінними X1 та X2.
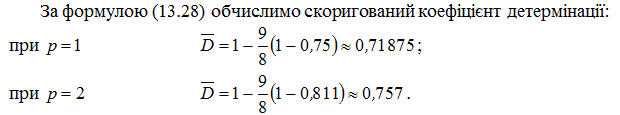
Легко бачити, що хоча скоригований коефіцієнт детермінації і збільшився при внесенні в модель пояснювальної змінної X2 (рівня механізації робіт), та це ще не свідчить про значущість коефіцієнта b2.


Завдання для самостійного виконання
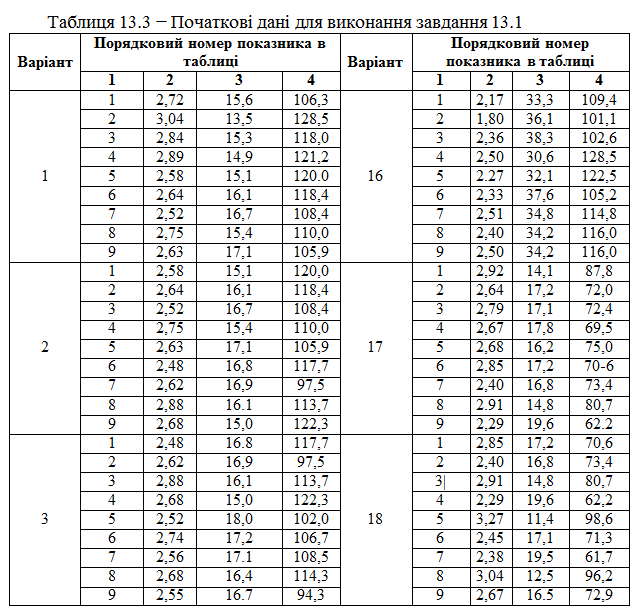
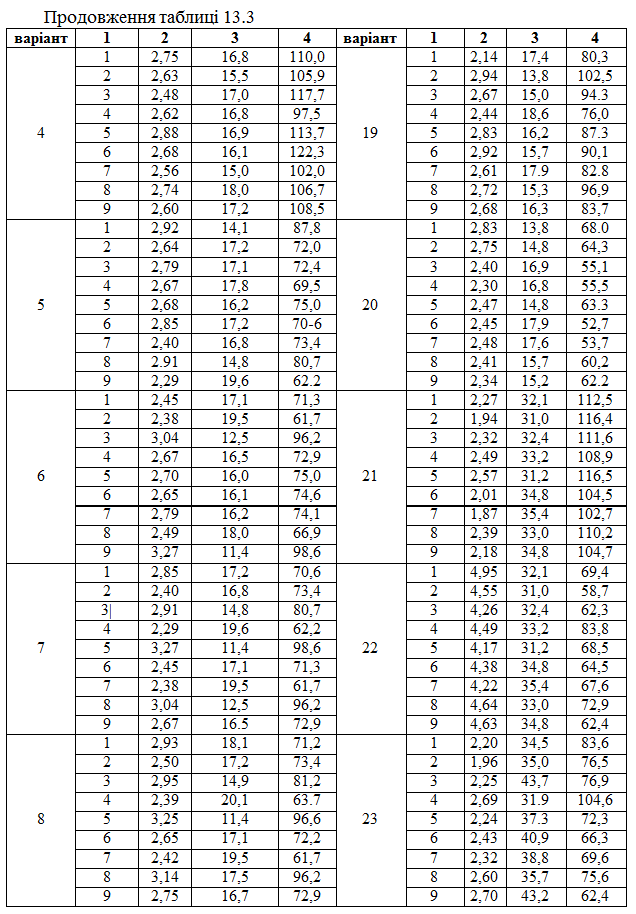
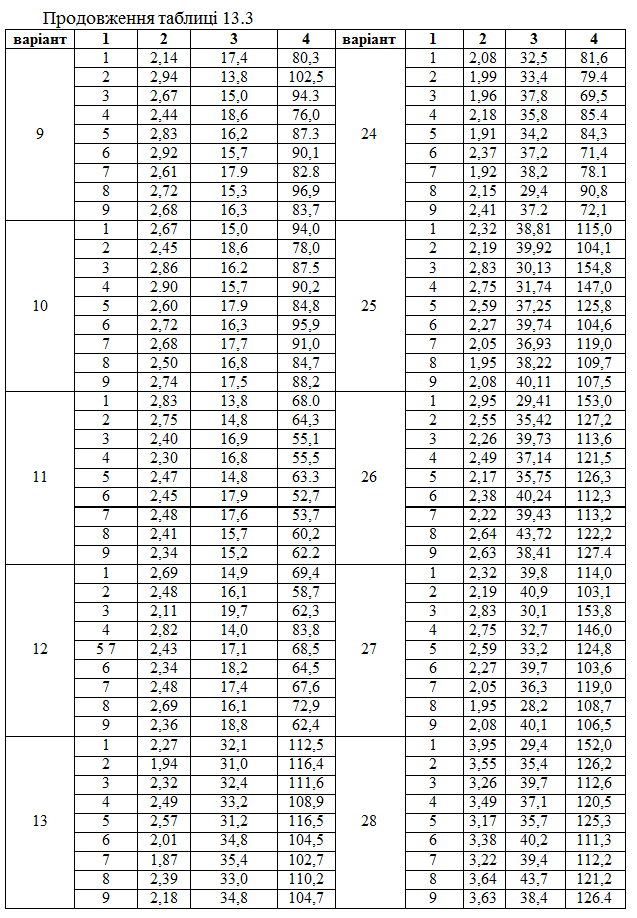
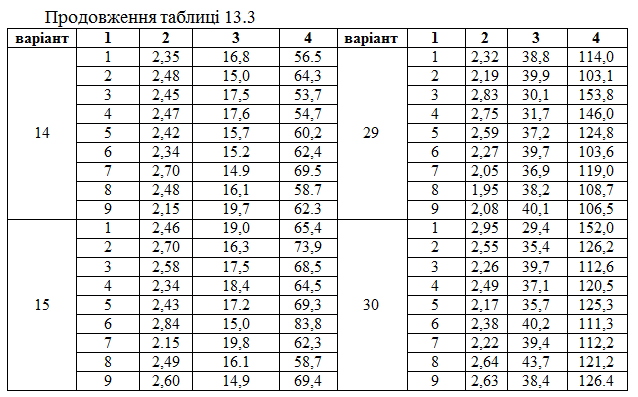
Порядковий номер показника, поданого у таблиці 13.3
1. Номер виміру.
2. Величина витрат, млн грн.
3. Показник вантажообігу, млн грн.
4. Показник фондомісткості.
2. Величина витрат, млн грн.
3. Показник вантажообігу, млн грн.
4. Показник фондомісткості.
Керуючись даними таблиці 13.3, потрібно
1. Побудувати лінійну економетричну модель, що характеризує залежність між витратами обігу, обсягом вантажообігу та фондомісткістю бази.
2. Визначити коефіцієнти еластичності та детермінації.
3. Зробити висновки.
2. Визначити коефіцієнти еластичності та детермінації.
3. Зробити висновки.
Питання для самоконтролю
1. Запишіть класичну нормальну лінійну модель множинної регресії у
звичайній та матричній формах.
2. Охарактеризуйте процес оцінювання параметрів класичної регресій¬ної моделі методом найменших квадратів. 3. Що характеризує коефіцієнт еластичності та як його можна обчислити?
4. Що називають коваріаційною матрицею? Запишіть її. Що пояснює коефіцієнт коваріації?
5. Охарактеризуйте коваріаційну матрицю вектора збурень.
6. Що таке коваріаційна матриця?
7. Сформулюйте та доведіть теорему Гаусса-Маркова.
8. Поясніть, що є дисперсією збурень.
9. Охарактеризуйте перевірку двофакторної регресії на адекватність за допомогою коефіцієнта детермінації.
10. Охарактеризуйте критерій Фішера.
2. Охарактеризуйте процес оцінювання параметрів класичної регресій¬ної моделі методом найменших квадратів. 3. Що характеризує коефіцієнт еластичності та як його можна обчислити?
4. Що називають коваріаційною матрицею? Запишіть її. Що пояснює коефіцієнт коваріації?
5. Охарактеризуйте коваріаційну матрицю вектора збурень.
6. Що таке коваріаційна матриця?
7. Сформулюйте та доведіть теорему Гаусса-Маркова.
8. Поясніть, що є дисперсією збурень.
9. Охарактеризуйте перевірку двофакторної регресії на адекватність за допомогою коефіцієнта детермінації.
10. Охарактеризуйте критерій Фішера.
Тестові завдання




