Зміст Наступна сторінка Електронні посібники ВНТУ
ЛАБОРАТОРНА РОБОТА № 1
ВИВЧЕННЯ ОСНОВНИХ ВЛАСТИВОСТЕЙ ІНФОРМАЦІЙНИХ ХАРАКТЕРИСТИК ДЖЕРЕЛ ТА КАНАЛІВ ПЕРЕДАЧІ ІНФОРМАЦІЇ
ВИВЧЕННЯ ОСНОВНИХ ВЛАСТИВОСТЕЙ ІНФОРМАЦІЙНИХ ХАРАКТЕРИСТИК ДЖЕРЕЛ ТА КАНАЛІВ ПЕРЕДАЧІ ІНФОРМАЦІЇ
Мета: засвоєння на практиці основних властивостей ентропії дискретних, неперервних та складних повідомлень.
1.1 Теоретичні відомості
1.1.1 Ентропія джерела дискретних повідомлень
У багатьох випадках, коли потрібно узгодити канал із джерелом повідомлень, недостатньо знати кількість інформації, що міститься в окремих повідомленнях. Виникає потреба у характеристиках, які б давали можливість оцінювати інформаційні властивості джерела повідомлень у цілому. Однією з таких важливих характеристик є середня кількість інформації одного повідомлення.
У найпростішому випадку, коли вcі повідомлення рівноймовірні, тобто P(ai)=1/m, середня кількість інформації дорівнює log m. Отже, при рівноймовірних незалежних повідомленнях інформаційні властивості джерела залежать тільки від числа повідомлень. Однак у реальних умовах повідомлення, як правило, мають різну ймовірність. Тому додатково потрібно мати відомості про ймовірності кожного повідомлення P (ai), i = 1, m .
Оскільки ймовірності повідомлень неоднакові, вони несуть різну кількість інформації. Менш імовірні повідомлення несуть більшу кількість інформації, і навпаки.
Середня кількість інформації одного повідомлення (біт/повідомлення) визначається як математичне сподівання:
Величина H(a) називається ентропією. Вона характеризується невизначеністю ситуації щодо передавання повідомлення, оскільки заздалегідь невідомо, яке саме повідомлення з повідомлень джерела буде передано. Чим більша ентропія, тим сильніша невизначеність, і тим більшу інформацію несе одне повідомлення джерела.
Ентропія як міра невизначеності скінченної системи повідомлень має такі основні властивості:
- У тому разі, коли повідомлення є рівноймовірними, зі збільшенням числа можливих подій m, що складають скінченну систему подій (повну групу), невизначеність цієї системи подій збільшується. Коли вcі повідомлення рівноймовірні [P(ai) = 1/m], ентропія системи дорівнює:
- Якщо ймовірність якого-небудь повідомлення дорівнює одиниці [P(ai)=1], то ентропія скінченної системи дорівнює нулеві.
- Невизначеність скінченної системи повідомлень при даному m максимальна при pівноймовірних повідомленнях.
- Ентропія має властивість адитивності, тобто невизначеність сполученої системи подій дорівнює сумі ентропій незалежних скінченних систем подій, що складають сполучену систему.
Джерела незалежних повідомлень є найпростішим типом джерел. У реальних умовах все значно ускладнюється через наявність статистичних зв’язків між повідомленнями.
Статистичний зв’язок очікуваного повідомлення з попереднім повідомленням кількісно оцінюється спільною P (ai, ak) або умовною ймовірністю P (ai / ak).
Кількість інформації, що міститься в повідомленні ai за умови, що попереднє повідомлення ak відоме,
Середня кількість інформації визначається умовною ентропією, яка обчислюється як математичне сподівання:
У загальному випадку для n залежних повідомлень:
1.1.2 Ентропія неперервних повідомлень
Неперервні повідомлення (наприклад, телефонні, телевізійні) успішно передаються каналами зв’язку з завадами та записуються завдяки тому, що на практиці ніколи не ставиться вимога точного відтворення переданого чи записаного повідомлення. А для передавання навіть з дуже високою, але обмеженою точністю, потрібна скінченна кількість інформації, як і для передавання дискретних повідомлень. Зрозуміло, ця кількість інформації тим більша, чим вища точність, з якою треба передати (відтворити) неперервне повідомлення. Нехай допустима точність вимірюється деяким параметром ε. Ту мінімальну кількість інформації, яку необхідно передати каналом зв’язку для відтворення неперервного повідомлення з неточністю, не більшою за допустиму, академік А. М. Колмогоров запропонував називати ε-ентропією (епсилон-ентропією).
При передаванні неперервних повідомлень передані сигнали s(t) є функціями часу, які належать до деякої множини, а отримані сигнали x(t) будуть їх реалізаціями.
Всі дійсні сигнали мають спектри, загальна енергія яких зосереджена в обмеженій смузі частот F. Згідно з теоремою В. О. Котельникова такі сигнали визначаються своїми значеннями в точках відліку, які вибирають через інтервали ∆t = 1/2F.
У каналі на сигнал накладаються завади, внаслідок чого кількість різних рівнів сигналу в точках відліку буде скінченною. Отже, сукупність значень неперервного сигналу еквівалентна деякій дискретній скінченній сукупності. Це дає змогу визначити необхідну кількість інформації та пропускну здатність при передаванні неперервних повідомлень, що базуються на результатах, отриманих для дискретних повідомлень.
Визначимо середню кількість інформації, яка міститься в одному відліку сигналу x відносно переданого сигналу s:
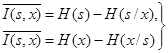
де H (s) = −![]() – диференціальна ентропія сигналу s;
– диференціальна ентропія сигналу s;
H (x) = −![]() – диференціальна ентропія сигналу x;
– диференціальна ентропія сигналу x;
H (s / x) = −∫∫ p(x , s) log p (s / x)ds dx– умовна диференціальна ентропія сигналу s;
H (x / s) = −∫∫ p(s , x) log p (x / s)ds dx– умовна диференціальна ентропія сигналу або ентропія шуму.
Величина H (s) характеризує інформаційні властивості сигналів, за формою записів вона аналогічна ентропії дискретних повідомлень.
Багато властивостей ентропії неперервного розподілу аналогічні властивостям ентропії дискретного сигналу.
Якщо неперервний сигнал s має рівномірний розподіл:
p (s) = 1/(s2 − s1)
та обмежений інтервалом s1≤s<s2 , то ентропія H(s) максимальна і дорівнює log(s2 − s1).
Диференціальна ентропія (на відміну від ентропії дискретних сигналів) залежить від розмірності неперервного сигналу, завдяки чому вона не є мірою кількості інформації, хоч і характеризує ступінь невизначеності, яка властива джерелу. Тільки різниця ентропій кількісно визначає середню кількість інформації.
1.1.3 Ентропія складних повідомлень, надмірність джерела
При передачі та зберіганні даних часто мають справу з кількома джерелами, що формують статистично пов’язані один з одним повідомлення. Повідомлення, що виробляються такими джерелами, називаються складними повідомленнями, а самі джерела — джерелами з пам’яттю.
Очевидно, що при визначенні ентропії і кількості інформації в повідомленнях, елементи яких статистично пов'язані, не можна обмежуватися тільки безумовними ймовірностями — необхідно обов’язково враховувати також умовні ймовірності появи окремих повідомлень.
Cпільна ентропія H(x,y) визначиться як:
де ![]() — так звана приватна умовна ентропія, що відображає ентропію повідомлення y за умови, що мало місце повідомлення xi.
— так звана приватна умовна ентропія, що відображає ентропію повідомлення y за умови, що мало місце повідомлення xi.
Другий доданок представляє собою усереднення ![]() по всім повідомленням xi і називається середньою умовною ентропією джерела у, за умови передачі повідомлення х.
по всім повідомленням xi і називається середньою умовною ентропією джерела у, за умови передачі повідомлення х.
І остаточно:
Таким чином, спільна ентропія двох повідомлень дорівнює сумі безумовної ентропії одного з них і умовної ентропії другого.
Можна відзначити наступні основні властивості ентропії складних повідомлень:
1. При статистично незалежних повідомленнях х і у спільна ентропія дорівнює сумі ентропій кожного з джерел.
2. При повній статистичній залежності повідомлень х і у спільна ентропія дорівнює безумовній ентропії одного з повідомлень. Друге повідомлення при цьому інформації не додає.
3. Умовна ентропія змінюється в межах ![]() .
.
4. Для спільної ентропії двох джерел завжди справедливе співвідношення: ![]() . При цьому умова рівності виконується тільки для незалежних джерел повідомлень.
. При цьому умова рівності виконується тільки для незалежних джерел повідомлень.
Отже, за наявності зв’язку між елементарними повідомленнями ентропія джерела знижується.
1.2 Завдання до лабораторної роботи
Використовуючи математичний пакет MathCad, виконайте завдання 1–5 за номерами варіантів. Розв’язок завдань з відповідними висновками відобразити у звіті.
1. Розрахуйте ентропію системи, що описується дискретною випадковою величиною х із наступним рядом розподілу, що наведені по варіантам табл. А.1 (додаток А).
2. Розрахуйте ентропію повідомлення із 5-ти букв, якщо загальна кількість букв в алфавіті дорівнює 32 і всі повідомлення рівноймовірні.
3. Розрахуйте диференціальну ентропію неперервного повідомлення, що розподілено за одним із законів, що наведені відповідно до варіантів табл. А.2 (додаток А).
4. Ймовірності появи повідомлень від першого джерела х (х![]() , х
, х![]() , х
, х![]() , х
, х![]() ) дорівнюють р(х
) дорівнюють р(х![]() )=0,1; р(х
)=0,1; р(х![]() )=0,025; р(х
)=0,025; р(х![]() )= 0,25; р(х
)= 0,25; р(х![]() )=0,125, а від другого джерела у (у
)=0,125, а від другого джерела у (у![]() , у
, у![]() , у
, у![]() , у
, у![]() ) — р(у
) — р(у![]() )=0,2; р(у
)=0,2; р(у![]() )=0,15; р(у
)=0,15; р(у![]() )=0,025; р(у
)=0,025; р(у![]() )=0,15, також відомі умовні ймовірності повідомлень табл.А.3 (додаток А). Розрахуйте об’єднану ймовірність появи повідомлень х та у і об’єднану ентропію сукупності повідомлень Х та У.
)=0,15, також відомі умовні ймовірності повідомлень табл.А.3 (додаток А). Розрахуйте об’єднану ймовірність появи повідомлень х та у і об’єднану ентропію сукупності повідомлень Х та У.
5. Ймовірності появи повідомлень від першого джерела х (х![]() , х
, х![]() , х
, х![]() , х
, х![]() ) дорівнюють р(х
) дорівнюють р(х![]() )=0,1; р(х
)=0,1; р(х![]() )=0,025; р(х
)=0,025; р(х![]() )=0,25; р(х
)=0,25; р(х![]() )=0,125, а від другого джерела у (у
)=0,125, а від другого джерела у (у![]() , у
, у![]() , у
, у![]() , у
, у![]() ) — р(у
) — р(у![]() )=0,2; р(у
)=0,2; р(у![]() )=0,15; р(у
)=0,15; р(у![]() )=0,025; р(у
)=0,025; р(у![]() )=0,15. Між повідомленнями існує кореляційний зв’язок табл.А.4 (додаток А). Розрахуйте умовну ймовірність появи повідомлень і умовну ентропію сукупності повідомлень х та у.
)=0,15. Між повідомленнями існує кореляційний зв’язок табл.А.4 (додаток А). Розрахуйте умовну ймовірність появи повідомлень і умовну ентропію сукупності повідомлень х та у.
1.3 Контрольні запитання
1. Що таке ентропія?
2. Що таке кількість інформації та як вона розраховується?
3. Назвіть основні властивості ентропії дискретних повідомлень.
4. Що таке диференціальна ентропія та для яких повідомлень вона застосовується?
5. Що таке об’єднана ентропія? Наведіть формулу для визначення об’єднаної ентропії сукупності повідомлень.
6. Назвіть основні властивості ентропії складних повідомлень.