Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

ЛАБОРАТОРНА РОБОТА № 3

ДОСЛІДЖЕННЯ ОСНОВНИХ ВЛАСТИВОСТЕЙ RC-ФІЛЬТРІВ НИЖНІХ ТА ВЕРХНІХ ЧАСТОТ

Мета: засвоєння на практиці основних властивостей RC-фільтрів нижніх і верхніх частот та дослідження їх принципів роботи.

3.1 Теоретичні відомості

3.1.1 Основні характеристики фільтра нижніх частот

Фільтри – це пристрої, які по-різному впливають на сигнали з різними частотами. Фільтри є найпоширенішими конструкціями в колах змінного струму. До назви фільтрів часто додають види елементів, що використовуються для їх побудови, зокрема RC-фільтри складаються лише з резисторів та конденсаторів.

За характером впливу на сигнали фільтри поділяють на:

• фільтри низьких частот (ФНЧ);
• фільтри високих частот (ФВЧ);
• смугові фільтри, які пропускають сигнали з частотами певного діапазону;
• режекторні фільтри, які пропускають сигнали з частотами, що не належать певному діапазону.

Якщо фільтр налагоджується на одну частоту його називають вузькосмуговим або фільтром-пробкою.

Властивості RC-фільтрів обумовлені залежністю від частоти ємнісного опору конденсаторів. Вони характеризуються простотою конструкції, малою вартістю, нечутливістю до магнітних полів, можливістю побудови малогабаритних схем для найнижчих частот тільки за рахунок збільшення номіналів резисторів.

   Фільтр нижніх частот (ФНЧ) є схемою, яка без змін передає сигнали нижніх частот, а на верхніх частотах забезпечує затухання сигналів і запізнення їх за фазою відносно вхідних сигналів. На рис. 3.1 наведена схема простого RC-фільтра нижніх частот.

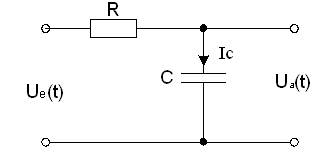
Для розрахунку частотної характеристики схеми використаємо формулу відношення напруг, представлених в комплексній формі:

       

.

       (3.1)

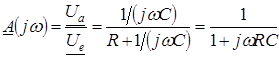   З виразу (3.1), враховуючи, що , отримаємо

       

;.

       (3.2)

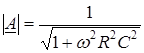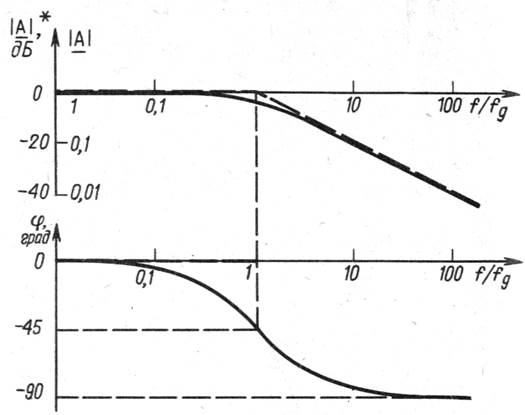
Залежності, що описуються формулою (3.2) представлені на рис. 3.2.

Підставивши , отримаємо вираз для визначення частоти зрізу

       

.

       (3.3)

Фазовий зсув j на такій частоті, відповідно до формули (3.2), складає – 45°.

Як видно з рис. 3.2, амплітудно-частотну характеристику  найпростіше скласти з двох асимптот:

1)  на нижніх частотах f <<f_g;

2) на високих частотах f>>f_g, відповідно до формули (3.2), , тобто коефіцієнт підсилення обернено пропорційний частоті.

При збільшенні частоти в 10 раз коефіцієнт підсилення зменшується в 10 раз (зменшується на 20 дБ на декаду або на 6 дБ на октаву);

3)  при f = f_g.

Для аналізу схеми в часовій області на вхід схеми (рис. 3.1) подається імпульс напруги (рис 3.3).

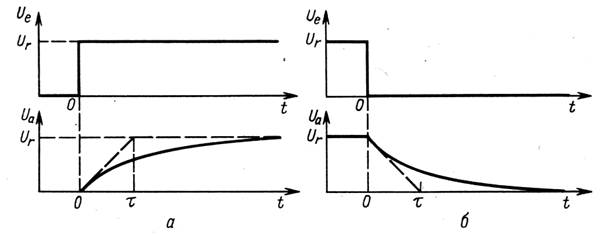
Щоб розрахувати вхідну напругу, використовується правило вузлів до ненавантаженого виходу. Тоді для схеми, що зображена на рис 3.1, запишемо:

       

.

       (3.4)

Враховуючи, що  отримаємо диференціальне рівняння:

       

       (3.5)

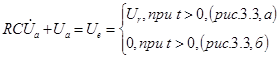
   Диференціальне рівняння (3.5) має такий розв’язок:

– для рис. 3.3, а:

       

;

       (3.6)

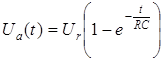– для рис. 2.3, б:

       

.

       (3.7)

Відомо, що для встановлених значень U_a=U_r i U_a=0 криві будуть наближатися асимптотично. Тому в якості міри часу установки вихідної напруги прийнята постійна часу t.

Вона показує інтервал часу, протягом якого процес досягає значення, що відрізняється від встановленого на  (частину величини стрибка напруги на вході). З формул 3.6, 3.7 видно, що постійна часу дорівнює:

       

.

       (3.8)

Іншим параметром, що характеризує ФНЧ, є тривалість інтервалу фронту імпульсу. Цей параметр показує час, на протязі якого вихідна напруга зростає від 10 до 90 % кінцевого значення, якщо на вхід подати імпульс напруги прямокутної форми. Враховуючи властивості експоненціальної функції, з формул 3.6, 3.7 отримаємо:

       

.

       (3.9)

При :

       

.

       (3.10)

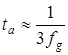Це співвідношення з високим ступенем точності дійсне для ФНЧ.

При послідовному з’єднанні декількох ФНЧ, що забезпечують різні тривалості фронту вихідного імпульсу t_i, результуюча тривалість фронту імпульсу дорівнює:

       

.

       (3.11)

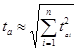Частота зрізу наближено визначається так:

       

       (3.12)

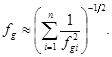
Для випадку з n фільтрами із рівними частотами зрізу:

       

.

       (3.13)

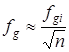3.1.2 Фільтр верхніх частот. Частота зрізу.

Фільтр верхніх частот  (ФВЧ) – це схема, яка передає без змін сигнали високих частот, а на низьких частотах забезпечує затухання сигналів і випередження їх за фазою відносно вхідних сигналів. Схема простого RC-фільтра верхніх частот наведена на рис. 3.4.

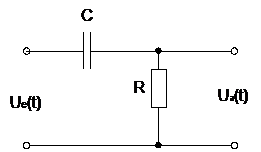
Амплітудно-частотні і фазочастотні характеристики отримаємо з формули для відношення напруг:

       

.

       (3.14)

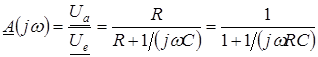З виразу (3.14) визначається:

       

 ;  .

       (3.15)

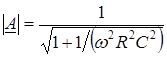Вираз для частоти зрізу співпадає з відповідним виразом для ФНЧ

       

.

       (3.16)

Фазовий зсув на цій частоті складає +45°. Як і для ФНЧ, найпростіше скласти АЧХ в подвійному логарифмічному масштабі за допомогою асимптот:

1)  на високих частотах f >>f_g;

2) на низьких частотах f <<f_g, відповідно до формули (3.15), , тобто коефіцієнт підсилення пропорційний частоті. Нахил асимптоти дорівнює +20 дБ на декаду або +6дБ на октаву.

3) При f = f_g, як і для ФНЧ

.

В результаті розрахунку реакції на імпульс напруги, постійна часу, як і для ФНЧ, дорівнює t=RC.

При послідовному з’єднанні ФВЧ результуюча частота зрізу визначається з виразу:

       

.

       (3.17)

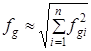   Для випадку з n фільтрів із рівними частотами зрізу:

       

.

       (3.18)

3.2 Опис лабораторного обладнання

Для експериментальних досліджень роботи RC-фільтрів використовується програма ElectronicsWorkbench, MicroCap або Proteus при побудові основних схем ввімкнення RC-фільтрів верхніх та нижніх частот. В цих програмних середовищах необхідно промоделювати роботу RC-фільтрів, схеми яких наведено в табл. 3.1.

При моделюванні схем фільтрації на вхід фільтрів необхідно подавати гармонічні сигнали за допомогою генератора напруги з амплітудою 1,5 В та несучою частотою для ФНЧ – 600 Гц, а для ФВЧ – 10 кГц.

Таблиця 3.1 – Схеми фільтрів різних типів

Тип фільтра		Назва	Схема
1	ФНЧ	Одноланковий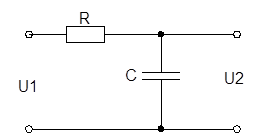
2	ФНЧ	Двохланковий
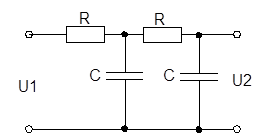
3	ФНЧ	Трьохланковий
4	ФВЧ	Одноланковий
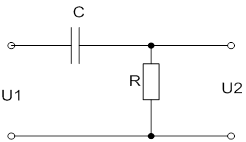
5	ФВЧ	Двохланковий
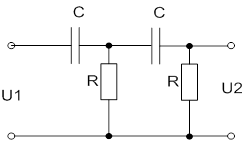
6	ФВЧ	Трьохланковий

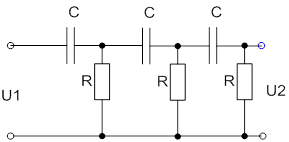
3.3 Завдання до лабораторної роботи

Для виконання лабораторної роботи оберіть свій варіант завдання  табл. В.1 (додаток В).

1. Виконайте розрахунки елементів опору R та ємності C для пропускання заданих частот, враховуючи, що канали зв’язку можуть приймати дискретний ряд значень опорів – 600, 150, 135 та 75 Ом.
2. Дослідити АЧХ та ФЧХ кожної з ланок фільтрів на заданих частотах.
3. Накласти на несучу частоту генератора напруги високочастотну складову на рівні 8 кГц при дослідженні ФНЧ, а при дослідженні ФВЧ на вхідну частоту генератора напруги накласти низькочастотну складову на рівні 800 Гц (амплітудне значення напруги високо- та низькочастотних складових прийняти рівним 0,5 В).

Дослідити роботу кожної з ланок фільтрів при накладанні частот та побудувати характеристики вхідних і вихідних сигналів, а також  АЧХ і ФЧХ  RC-фільтрів.

4. Розрахувати рівні передачі одно-, двох- і трьох-ланкових фільтрів верхніх та нижніх частот, шляхом вимірювання напруг на вході та виході фільтрів.

За результатами вимірювань та розрахунків зробити висновки, які доводять, що фільтри з більшою кількістю ланок мають кращі характеристики.

Зробіть загальні висновки за результатами досліджень RC-фільтрів нижніх та верхніх частот.

3.4 Вказівки до звіту

Звіт з лабораторної роботи повинен містити:

• розрахунки частот зрізу RC-фільтрів;
• результати досліджень вхідних та вихідних сигналів, а також їх АЧХ і ФЧХ всіх видів RC-фільтрів (табл. 3.1);
• результати досліджень основних характеристик RC-фільтрів при накладанні високо та низько частотних складових частот на вхідні частоти;
• результати розрахунків рівнів передачі фільтрів;
• загальні висновки по роботі.

3.5 Контрольні запитання

1. Що називається фільтром нижніх частот?
2. Що називається фільтром верхніх частот?
3. Назвіть основні характеристики фільтра нижніх та верхніх частот.
4. Що таке частота зрізу та як вона визначається?
5. Як визначити тривалість частоти зрізу та частоту зрізу при послідовному з’єднанні декількох фільтрів нижніх частот?
6. Як визначається частота зрізу при послідовному з’єднанні декількох фільтрів верхніх частот?
7. Як впливає метод апроксимації частотної характеристики фільтра на його параметри та схему?
8. Якими параметрами визначається конструкція фільтра та технологія його використання?