3.2 Приклади розв’язання задач

Задача 3.2.1

Пластина розмірами 0,91,5 м обдувається повітрям, температура якого 20 ^оС, а швидкість 0,2 м/с. Визначити тепловий потік від пластини до повітря, якщо температура стінки пластини 80 ^оС.

Розв’язування

Теплофізичні властивості повітря для t_п = 20 ^оС (додаток Г): λ = 0,0259 Вт/(м·К); ν = 15,06·10^-6 м²/с; Pr = 0,703.

Критерій Рейнольдса

     .

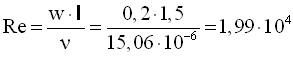Оскільки Re < 10⁵, то режим обтікання пластини ламінарний. Критерій Нуссельта визначаємо за (3.6)

     .

Середній коефіцієнт тепловіддачі від стінки до повітря, Вт/(м²·К)

     .

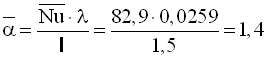Тепловий потік, Вт

     .

Задача 3.2.2. Вздовж пластини довжиною 5 м рухається вода з температурою 20 ^оС. Визначити питомий тепловий потік, а також товщину приграничного шару на відстані 0,5, якщо температура пластини 100 ^оС, а швидкість води 1 м/с.

Розв’язування

Теплофізичні властивості води для t_в = 20 ^оС (додаток В):
λ = 0,599 Вт/(м·К); ν = 1·10^-6 м²/с; Pr_р = 7,02, Pr_с = 1,75.

Критерій Рейнольдса

     .

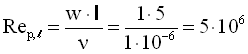Оскільки Re > 10⁵, то режим течії води турбулентний.

Критерій Нуссельта визначається за (3.7)

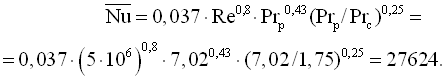
Середній коефіцієнт тепловіддачі від стінки до води, Вт/(м²·К)

     .

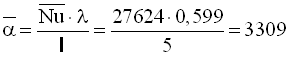Питомий тепловий потік, кВт/м²

     .

Для відстані х = 0,5 = 0,5·5 = 2,25 м критерій Рейнольдса буде

     .

Товщина приграничного шару за (3.3), м

     .

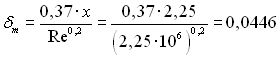Середнє значення критерію Нуссельта

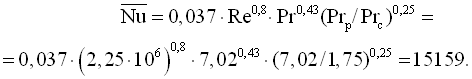
Середнє значення коефіцієнта тепловіддачі, Вт/(м²·К)

     .

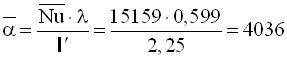Задача 3.2.3. В трубі з внутрішнім діаметром 9 мм і довжиною 3 м тече вода зі швидкістю 0,1 м/с. Середні значення температур стінки труби і води 20 і 60 ^оС, відповідно. Визначити середній коефіцієнт тепловіддачі від стінки труби до води.

Розв’язування

Теплофізичні властивості води для t_в = 60 ^оС (додаток В):
λ = 0,659 Вт/(м·К); ν = 4,78·10^-7 м²/с; β = 5,11·10^-4 К^-1; Pr_р = 2,98, Pr_с = 7,02.

Критерій Рейнольдса

     .

Оскільки Re < 2300, то режим руху ламінарний. Для визначення впливу природної конвекції необхідно визначити критерій Релея. При цьому за визначальну температуру треба брати середню температуру

     ^оС.

Критерій Релея

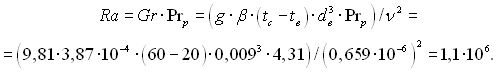
Оскільки , то природна конвекція впливає на теплообмін, а критерій Нуссельта визначається за (3.10)

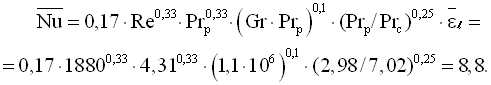
Тут ε_ℓ = 1, оскільки .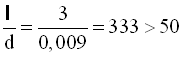

Середній коефіцієнт тепловіддачі, Вт/(м²·К)

     .

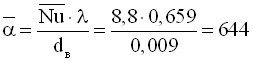Задача 3.2.4. В кільцевому каналі (ring canal), утвореному трубами діаметром D_вн = 60 мм і d_зн = 50 мм тече вода зі швидкістю 1 м/с і температурою 10 ^оС. Середня температура стінки становить 60 ^оС. Визначити питомий та лінійний тепловий потоки.

Розв’язування

Еквівалентний діаметр кільцевого каналу, м

     .

Теплофізичні властивості води для t_в = 20 ^оС (додаток В):
λ = 0,599Вт/(м·К); ν = 1,306·10^-6 м²/с; Pr_р = 9,52, Pr_с = 2,98.

Критерій Рейнольдса

     .

Для визначення критерію Нуссельта використовуємо рівняння (3.12)

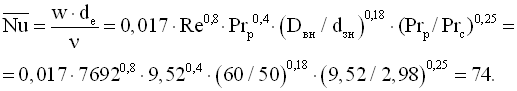
Середній коефіцієнт тепловіддачі, Вт/(м²·К)

     .

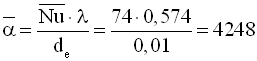Питомий тепловий потік, кВт/м²

     .

Поверхня теплообміну одного погонного метра каналу, м²/м

     .

Лінійний тепловий потік, кВт/м

     .

Визначимо тепер коефіцієнт тепловіддачі за формулою (3.11), зважаючи на те, що Pr > 2 і вводячи поправковий коефіцієнт ε_п із табл. 3.3.

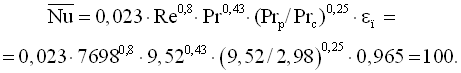
Середній коефіцієнт тепловіддачі, Вт/(м²·К)

     .

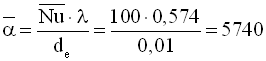Як видно розбіжність складає 26 %. Отже, формулу (3.11) краще застосовувати для обчислення теплообміну в трубах.

Задача 3.2.5. Вода з початковою температурою 10 ^оС рухається зі швидкістю 2 м/с в трубі з внутрішнім діаметром 16 мм. Середня температура стінки труби становить 30 ^оС. Визначити тепловий потік і довжину труби, якщо температура води на виході з труби дорівнює 20 ^оС.

Розв’язування

Середня температура води

     .

Теплофізичні властивості води для середньої температури t_в = 15 ^оС (додаток В): λ_в = 0,5865 Вт/(м·К); ν_в = 1,15·10^-6 м²/с; Pr_р = 8,27, Pr_с = 5,66,
С_р = 4,148 кДж/(кг·К), ρ_в = 999 кг/м³.

Критерій Рейнольдса

     .

Режим течії турбулентний. Критерій Нуссельта визначаємо за (3.11). Оскільки довжина труби невідома, то поправковий коефіцієнт ε_ℓ в першому наближенні беремо рівним одиниці. Тоді для Pr > 2 одержимо

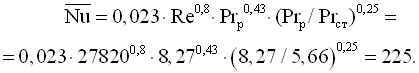
Середній коефіцієнт тепловіддачі, Вт/(м²·К)

     .

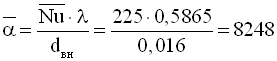Площа поперечного перерізу труби, м²

     .

Масова витрата води в трубі, кг/с

     .

Тепловий потік до води, кВт

     .

Середньологарифмічний температурний напір, ^оС

     .

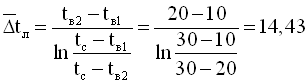Довжина труби, м

     .

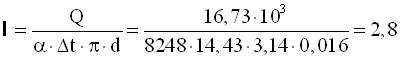Оскільки /d = 2,79/0,016=174,6 > 50, то розрахунки уточнювати не потрібно.

Задача 3.2.6. Вода зі швидкістю 0,75 м/с і температурою 30 ^оС надходить в трубу діаметром 12 мм. Визначити температуру води на виході з труби, якщо довжина труби 2,2 м, а температура внутрішньої стінки труби 60 ^оС.

Розв’язування

Для обчислення коефіцієнта тепловіддачі необхідно знати середню температуру води в трубі. Оскільки температура води на виході з труби невідома, то задачу розв’язуємо методом послідовних наближень. Беремо температуру води на виході з труби 50 ^оС.

Середня температура води, ^оС

     .

Теплофізичні властивості води для середньої температури t_в = 40 ^оС (додаток В): λ = 0,634 Вт/(м·К); ν = 0,659·10^-6 м²/с; Pr_р = 4,31; Pr_с = 2,98;
С_р = 4,174 кДж/(кг·К), ρ = 992 кг/м³.

Критерій Рейнольдса

     .

Режим течії турбулентний. Критерій Нуссельта визначаємо за (3.11). для Pr > 2

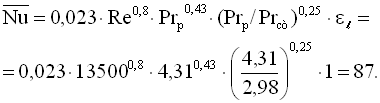
Середній коефіцієнт тепловіддачі, Вт/(м²·К)

     .

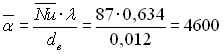Площа поперечного перерізу труби, м²

     .

Масова витрата води в трубі, кг/с

     .

Площа поверхні теплообміну, м²

     .

Тепловий потік, Вт

     ,

де – середньологарифмічний температурний напір, ^оС

Підстановка числових даних в останнє рівняння дає:

     .

Звідки    

або     .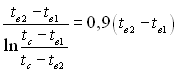

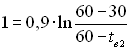
і t_в2 = 50,2 ^оС.

Оскільки розбіжність між вибраним і отриманим значеннями температури води на виході із труби не перевищує 1%, то розрахунки уточнювати не потрібно.

Задача 3.2.7. За умови задачі 3.2.6 визначити, як зміниться коефіцієнт тепловіддачі, якщо трубу, в якій тече вода, виконати у вигляді змійовика з радіусом вигину 120 мм.

Розв’язування

Визначимо співвідношення:

     ;

     ;

     ;

     .

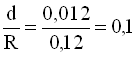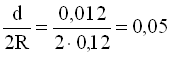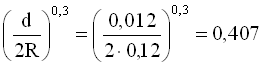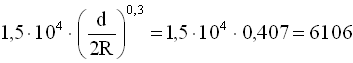Оскільки критерій Ренольдса в задачі 3.2.6 Re = 13500, тобто більший останньої величини, то поправковий коефіцієнт становитиме

     .

Коефіцієнт тепловіддачі, Вт/(м²·К)

     .

Задача 3.2.8. Вода з середньою температурою 150 ^оС рухається в трубі діаметром 20 мм і довжиною 2,3 м. Визначити, з якою швидкістю треба прокачувати воду, щоб в разі турбулентного режиму її течії тепловий потік дорівнював 8,7 кВт. Визначити також температуру води на вході в трубу та виході з неї, якщо температура стінки труби дорівнює 170 ^оС і підтримується сталою.

Розв’язування

В першому наближенні вважаємо, що середній температурний напір дорівнює, ^оС

     .

Коефіцієнт тепловіддачі від стінки до води, Вт/(м²·К)

     .

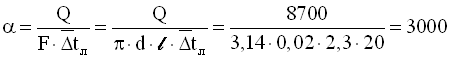Теплофізичні властивості води для t_в = 150 ^оС (додаток В): С_р = 4,31 кДж/(кг·К); ρ = 917 кг/м³; λ = 0,682 Вт/(м·К); ν = 0,2·10^-6 м²/с; Pr_р = 1,17; Pr_с = 1,05.

Критерій Нуссельта

     .

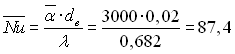Для турбулентного режиму руху із (3.11) визначаємо

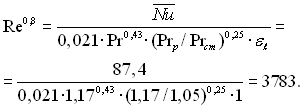
Звідки Re = 3·10⁴.

Швидкість води в першому наближенні, м/с

.

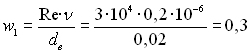Масова витрата води в трубі, кг/с

     .

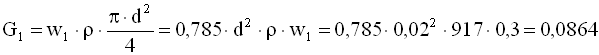Підігрів води в трубі, ^оС

     .

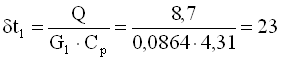Початкова і кінцева температури води, ^оС

     ;

     .

Середньологарифмічний температурний напір, ^оС

     .

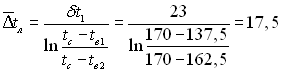Розбіжність між вибраним і розрахунковим температурним напором складає 12,7%. Тому для другого наближення беремо `Δt_в = 17,5 ^оС.

Результати розрахунків для другого наближення такі: α = 3400 Вт/(м²·К); Re₂ = 3,5·10⁴; G₂ = 0,182 кг/с; δt₂ = 19,9 ^оC; t_в1 ≈ 140 ^оС;  t_в2 ≈ 160 ^оС; `Δt<sub>в</sub> = 18,2 <sup>о</sup>С. Розбіжність між вибраним і розрахунковим `Δt_в становить 9%.

Для третього наближення беремо `Δt<sub>в</sub> = 18,2 <sup>о</sup>С. Результати розрахунків такі: α = 3300 Вт/(м<sup>2</sup>·К); Re<sub>3</sub> = 3,45·10<sup>4</sup>; G<sub>3</sub> = 0,191 кг/с; δt<sub>3</sub> = 20 <sup>о</sup>C; t<sub>в1</sub> ≈ 140 <sup>о</sup>С; t<sub>в2</sub> ≈ 160 <sup>о</sup>С; `Δt_в = 18,19 ^оС. Останнє значення `Δt_в практично збігається з останнім вибраним значенням.