4.2 Приклади розв’язання задач
Задача 4.2.1. Дріт з алюмінію діаметром 6 мм охолоджується поперечним потоком повітря з температурою 10 оС. Швидкість руху повітря 1 м/с. Визначити температуру дроту і необхідну силу струму, якщо питомий електричний опір алюмінію ρ = 2,86·10-8 Ом·м, а тепловий потік 2,7 кВт/м2.
Розв’язування
Теплофізичні властивості повітря для tп = 10 оС (додаток Г): λ = 0,0251 Вт/(м·К); ν = 14,16·10-6 м2/с; Prр = 0,705.
Критерій Рейнольдса
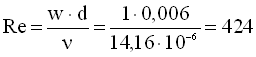 .
.
Оскільки ![]() , то критерій Нуссельта визначаємо за (4.5)
, то критерій Нуссельта визначаємо за (4.5)
![]() .
.
Середній коефіцієнт тепловіддачі від дроту до повітря, Вт/(м2·К)
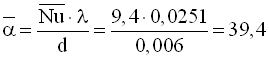 .
.
Температура на поверхні дроту, оС
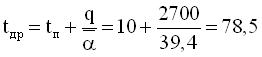 .
.
Електричний опір дроту, Ом
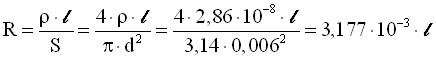 .
.
Тепловий потік, Вт
![]() ,
,
![]() .
.
Допустима сила струму, А
 .
.
Задача 4.2.2. Труба із зовнішнім діаметром 25 мм охолоджується поперечним потоком (φ = 90о) трансформаторного масла з температурою 20 оС. Визначити необхідну температуру стінки труби за умови, що швидкість масла 1 м/с, а питоме тепловідведення 45 кВт/м2.
Розв’язування
Теплофізичні властивості трансформаторного масла для tм = 20 оС (додаток Ж): λ = 0,11 Вт/(м·К); ν = 22,5·10-6 м2/с; Prр = 298.
Критерій Рейнольдса
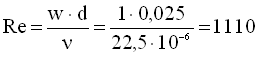 .
.
Оскільки ![]() , то використовуємо рівняння (4.6)
, то використовуємо рівняння (4.6)
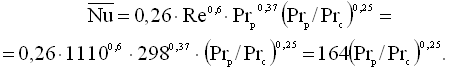
Через те, що останній вираз містить невідому величину Prс, то задача розв’язується графо-аналітичним методом. Беремо три значення температури стінки: tc1 = 40 оC; tc2 = 60 оC; tc3 = 80 оC. Для таких температур значення Prс будуть дорівнювати 146, 87,8, 59,3, відповідно. Тоді
![]() ;
;
![]() ;
;
![]() .
.
Коефіцієнти тепловіддачі, Вт/(м2·К):
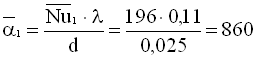 ;
;
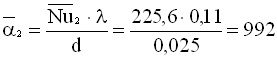 ;
;
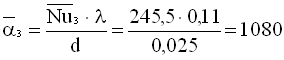 .
.
Питомі теплові потоки, кВт/м2:
![]() ;
;
![]() ;
;
![]() .
.
Будуємо залежність q = f(tc), яка показана на рис. 4.1.
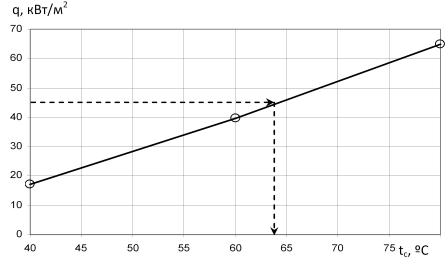
Рисунок
4.1 –
Залежність питомого теплового
потоку від температури стінки труби
Із рис. 4.1 для заданого теплового потоку (q = 45кВт/м2/sup>) визначаємо
tc = 64,5 оС.
Тоді Prc = 84; 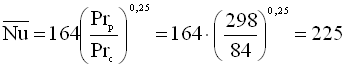 .
.
Середній коефіцієнт тепловіддачі від стінки труби до масла, Вт/(м2·К)
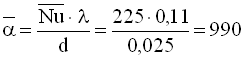 .
.
Задача 4.2.3. Підігрівник води виготовлений із труб діаметрами 30/26 мм. Труби розташовані в шаховому порядку з поперечним і повздовжнім кроком S1 = S2 = 2,5d. Кількість труб в ряду z = 8, кількість рядів труб n = 6. Температури грійного повітря t1 = 400 оC, t2 = 300 оC, середня температура стінок труб tс = 150 оC. Визначити довжину труб підігрівника, якщо його потужність 260 кВт, а швидкість повітря 10 м/с.
Розв’язування
Середня температура повітря, оС
![]() .
.
Теплофізичні властивості повітря для середньої температури
t = 350 оС (додаток Д):
λ = 0,049 Вт/(м·К);
ν = 55,46·10-6 м2/с; Prр = 0,676.
Критерій Рейнольдса
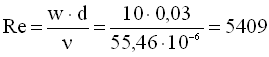 .
.
За таких умов сталі в критеріальному рівнянні (4.8) згідно з табл. 4.2 дорівнюватимуть С = 0,4; n = 0,6; εc = 11/6 = 1. Тоді критеріальне рівняння буде мати вигляд
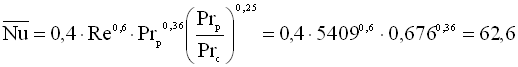 .
.
Коефіцієнт тепловіддачі до третього ряду, Вт/(м2·К)
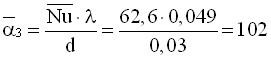 .
.
Середній коефіцієнт тепловіддачі в пучку, Вт/(м2·К)
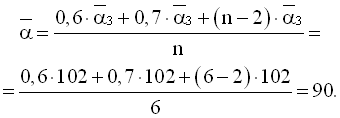
Питомий тепловий потік, кВт/м2
![]() .
.
Необхідна поверхня нагріву, м2
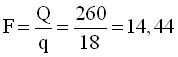 .
.
Необхідна довжина труби в апараті, м
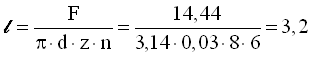 .
.
Задача 4.2.4. Трубчастий підігрівник являє собою коридорний пучок труб зовнішнім діаметром 38 мм і довжиною 3 м. Поперечний і повздовжний кроки в пучку становлять S1 = S2 = 2,3d. Кількість рядів труб z = 5, кількість труб в одному поперечному ряді n = 8. Повітря підігрівається від 20 до 80 оС. Температура зовнішньої поверхні труб підтримується рівною 150 оС. Визначити теплову потужність повітропідігрівника, якщо швидкість повітря 10 м/с.
Розв’язування
Середня температура повітря, оС
![]() .
.
Теплофізичні властивості повітря для середньої температури tпов = 50 оС (додаток Г): λпов = 0,0283 Вт/(м·К); νпов = 17,95·10-6 м2/с; Prр = 0,7.
Критерій Рейнольдса
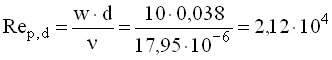 .
.
За умови ![]() критеріальним рівнянням буде рівняння (4.8), яке буде мати вигляд
критеріальним рівнянням буде рівняння (4.8), яке буде мати вигляд
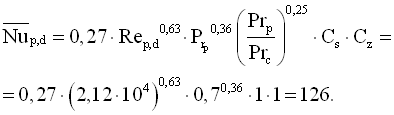
Коефіцієнт тепловіддачі до третього ряду труб, Вт/(м2·К)
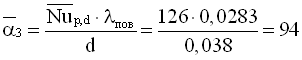 .
.
Середнє значення коефіцієнта εz за (4.9)
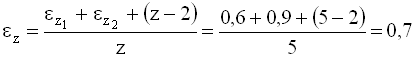 .
.
Середній коефіцієнт тепловіддачі в пучку, Вт/(м2·К)
![]() .
.
Питомий тепловий потік, Вт/м2
![]() .
.
Поверхня нагріву повітронагрівника, м2
![]() .
.
Потужність повітронагрівника, кВт
![]() .
.
Задача 4.2.5. Нагрівний пристрій являє собою корпус з розмірами 0,8![]() 1,25 м, в якому в коридорному порядку розташовані оребрені труби. Діаметр труб 20 мм, а поперечний крок між ними S1 = 50 мм. Висота ребер 10 мм, крок між ребрами 5 мм, а товщина ребер 1 мм. Труби поперечно обтікає повітря з температурою 50 оС і витратою 5,68 кг/с. Визначити середній коефіцієнт тепловіддачі для круглих і квадратних ребер.
1,25 м, в якому в коридорному порядку розташовані оребрені труби. Діаметр труб 20 мм, а поперечний крок між ними S1 = 50 мм. Висота ребер 10 мм, крок між ребрами 5 мм, а товщина ребер 1 мм. Труби поперечно обтікає повітря з температурою 50 оС і витратою 5,68 кг/с. Визначити середній коефіцієнт тепловіддачі для круглих і квадратних ребер.
Розв’язування
Площа поперечного перерізу корпусу нагрівника, м2
![]() .
.
Площа вузького перерізу для проходу повітря за (4.11)
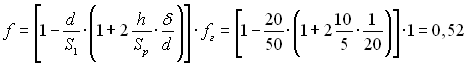
Середня температура повітря, оС
![]() .
.
Теплофізичні властивості повітря для середньої температури t = 50 оС (додаток Д): λ = 0,0283 Вт/(м·К); ν = 17,95·10-6 м2/с; Prр = 0,7.
Швидкість повітря у вузькому перерізі нагрівника, м/с
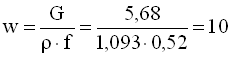 .
.
Критерій Рейнольдса
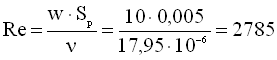 .
.
Відношення
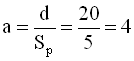 ;
; 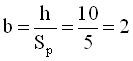 .
.
Критерій Нуссельта для труб з круглими ребрами за (4.10) із табл. 4.3.
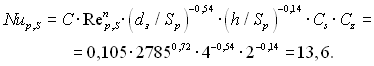
Коефіцієнт тепловіддачі для оребреної поверхні з круглими ребрами, Вт/(м2·К)
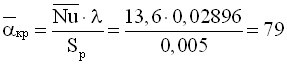 .
.
Для оребреної поверхні з квадратними ребрами
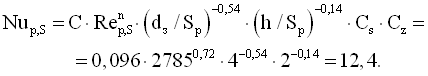
Коефіцієнт тепловіддачі для оребреної поверхні з квадратними ребрами, Вт/(м2·К)
![]() .
.


