Розділ 22. КРИЗА ТЕПЛОВІДДАЧІ ПРИ КИПІННІ В УМОВАХ ВІЛЬНОГО РУХУ

22.1. Рівняння подібності для визначення критичних теплових навантажень

Криза теплообміну при бульбашковому кипінні обумовлена зміною механізму тепловіддачі при переході від бульбашкового кипіння до плівкового. З підвищенням густини теплового у певний момент часу коефіцієнт тепловіддачі досягає максимуму, а далі відбувається зменшення інтенсивності теплообміну, яке супроводжується більш (при низьких тисках) чи менш (при високих тисках) різким збільшенням темпу росту температури поверхні теплообміну.

Проблема кризи тепловіддачі при бульбашковому кипінні (першій критичній густині теплового потоку q_кр) у строго спряженій постановці навіть у квазістаціонарних умовах (при повільному збільшенні q) повинна розглядатися з урахуванням властивостей рідини, пари і поверхні тепловіддачі. Але розв’язок її у загальному вигляді представляє великі труднощі. Тому поки приходиться обмежуватися пошуком наближеного рішення проблеми без урахування характеристик поверхні нагріву. При цьому можливі два основних підходи і дві фізичні моделі, які з цього витікають. Перший підхід ґрунтується на тому, що характерна для бульбашкового кипіння висока інтенсивність теплообміну

зберігається доти, поки внаслідок збільшення теплового навантаження не буде досягнуто певне граничне заповнення поверхні нагріву паровими бульбашками – граничний паровміст двофазного пристінного шару. Критичній густині теплового потоку відповідає певна гранична кількість діючих центрів пароутворення.

Такий підхід є природним і правомірним. Оскільки ставиться задача про кризу тепловіддачі при бульбашковому кипінні, то необхідно виходити з факту існування цього виду кипіння. Правомірність такої концепції підтверджується результатами дослідів, які свідчать про те, що при виникненні кризи тепловіддачі на поверхні нагріву ще існує двофазний шар. Другий підхід оснований на розгляді кризи як гідродинамічного явища. Згідно з таким уявленням криза настає тоді, коли припиняється доступ рідини до поверхні нагріву і настає стійке плівкове кипіння (відбувається відтискування рідини від поверхні нагріву суцільним паровим шаром).

Узагальнююча залежність для критичної густини теплового потоку q_кр отримана на основі теорії подібності і по суті у відповідності з першим підходом до проблеми. Гідродинамічна модель кризи теплообміну при кипінні, ґрунтується на другому підході, запропонована С.С.Кутаткладзе. Отримана ним узагальнююча залежність для визначення q_кр містить у собі знайдений ним з дослідів числовий коефіцієнт, значення якого коливаються в межах 0,09...0,2. При цьому досягається узагальнення дослідних даних з q_кр для багатьох рідин. Але для деяких рідин ця залежність не дає задовільного результату.

Узагальнюючу залежність для знаходження q_кр при кипінні насичених рідин за умов вільного руху можна отримати на загальній підставі з рівняння подібності процесу бульбашкового кипіння, яке враховує специфічні особливості цього процесу – його періодичність. Це – наведене раніше рівняння (20.13):

Nu = Nu(K, Fo, Pr, ℓ_*, r_*).

З рівняння (20.13) можна отримати узагальнюючу залежність для знаходження q_кр. У задачі про q_кр число Nu, як визначальна величина, з розгляду випадає, а число подібності К = q/rr_nd_вf стає визначальним (d_вf – середня швидкість росту парових бульбашок; d_в – відривний діаметр; f – частота утворення і відриву бульбашок). Зі збільшенням густини теплового потоку збільшується кількість діючих центрів пароутворення п і число К. Критичній густині теплового потоку відповідає граничне п і граничне значення К, рівне К_кр. При цьому паровміст пристінного шару значно менший 100%. Таким чином, з рівняння (20.13) виходить, що

К_кр = К_кр(Fo, Pr, ℓ_*, r_*). (22.1)

У межах наближеного аналізу і розв’язку задачі на підставі теорії подібності рівняння (22.1) можна спростити. З дослідів по визначенню q_кр виходить, що вплив в’язкості рідини і числа Pr на q_кр чи не проявляються взагалі, чи проявляється в малій мірі. Виходячи з цього, число Pr у рівнянні (22.1) можна випустити. Те саме стосується і ℓ_*, величина якого зв’язана з розміром відривного діаметра d_в. Якщо q_кр визначається граничним заповненням поверхні нагріву паровими бульбашками і їх накопиченням, то абсолютний розмір d_в не повинен відігравати суттєвої ролі, тому що не має великого значення чи буде заповнення досягнуте при великій кількості бульбашок малого діаметра, чи при малій кількості бульбашок великого діаметра. Виходячи з цього величиною ℓ_* нехтуємо. Тоді

К_кр = К_кр(Fo, r_*). (22.2)

Запишемо цю залежність у вигляді степеневої функції, отримаємо:

(22.3)

де

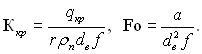
Значення показника т₁ визначається наступним чином. Якщо величина d_в не відіграє значної ролі і q_кр не залежить від d_в, то показник степеню т₁ повинен бути рівним 0,5:

(22.4)

(22.5)

Рівняння (22.5) має певний фізичний зміст. величина rr_n представляє собою об’ємну теплоту пароутворення, віднесену до 1 м³ пари. чим більше rr_n, тим вища густина теплового потоку при однаковому об’ємі отриманої пари. Тому, чим більше rr_n, тим при інших рівних умовах вище q_кр.

Тепловий потік, який відводиться при кипінні від поверхні нагріву, складається з теплових потоків, які переносяться рідиною і парою. Чим більший коефіцієнт теплопровідності і температуропровідності рідини, тим більша частина теплоти переноситься рідиною і відповідно менша частина теплоти відводиться парою. У зв'язку з цим зменшується паровміст пристінного шару при даній загальній густині теплового потоку. Отже, між величиною q_кр і коефіцієнтом температуропровідності рідини а повинна бути пряма залежність, що і відображає рівняння (22.5). Помітну роль повинна відігравати також частота утворення і відриву парових бульбашок від поверхні нагріву. Чим більша f, тим швидше парова фаза залишає пристінний шар і тим менший, при інших рівних умовах, паровміст двофазного пристінного шару. Тому із зміною f повинна змінюватися у тому ж напрямку і величина q_кр.

Щоб розкрити зміст симплексу r_* необхідно взяти до уваги наступне. Якісно залежність між q_кр і rr_n знаходить відображення в рівнянні (22.5) правильно, але величина rr_n для даної рідини є функцією тиску, і наряду з її зміною при зміні тиску змінюється також роль інших факторів, вплив яких не можна відтворити тільки величиною rr_n.

Як уже відмічалося, дуже суттєвим фактором є частка теплоти, яка відводиться від поверхні нагріву парою. У широкому інтервалі зміни тиску вона, як і величина rr_n, зростає з підвищенням тиску. Чим ця частка більша, тим при інших рівних умовах більший паровміст пристінного шару і відповідно менш досягнете q_кр. Тому симплекс r_* повинен бути функцією тиску, який відображає цей бік процесу. Таким симплексом є величиною, що зменшується зі зростанням тиску, і відтворюється відношенням густин r /r_п. Цей симплекс має також більш загальний зміст, тому що характеризує ступінь віддаленості рідини від критичної точки. При цьому рівняння (22.4) набуває вигляду:

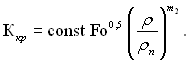(22.6)

22.2. Узагальнення даних для критичного теплового потоку

Дослідних даних по середнім значенням частот відриву f і відривних діаметрах d_в ансамблю парових бульбашок поки що накопичено мало. Але ті дані, які є зараз дозволяють з певним наближенням підійти до розв’язку поставленої задачі. У табл. 22.1 наведені деякі реперні значення частоти відриву бульбашок при кипінні різних рідин. Ці дані, а також загальні міркування про закономірності процесу кипіння дозволяють виявити наближену залежність f від П. Ясно, що при наближенні до критичної точки величини d_в, f і d_вf прямують до нуля. У той же час, дані наведені у таблиці, свідчать про те, що досить у широкому діапазоні П частота утворення і відриву бульбашок не сильно змінюється і знаходиться біля 100 1/с (за винятком води, для якої f =60...70 1/с). Можна вважати, що значне зменшення частоти розпочинається при П » 20. На підставі цих міркувань і наявних дослідних даних отримані орієнтовні залежності f =f (П) для води і інших рідин (крім металевих), наведених на рис.22.1.

Таблиця 22.1

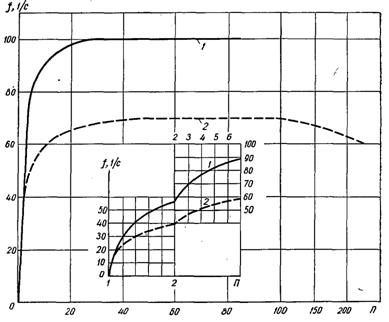
Рис.22.1. Осередненні залежності f від П: 1 – органічні і неорганічні (криогенні) рідини; 2 – вода

Величина середнього відривного діаметра парової бульбашки d_в зменшується приблизно обернено пропорційно тиску. Аналіз дослідних даних показує, що така пропорційність існує при П > 5. Починаючи з П = 5 до критичної точки залежності d_в = d_в(П) екстраполювалася графічним шляхом. Варто зауважити, що оскільки з розрахункової формули величина d_в випадає, то великої точності у її визначенні немає необхідності.

Опрацювання і узагальнення дослідних даних, по відомих з літературних першоджерел дослідним значенням q_кр, виконане на підставі залежності (22.1) для різних органічних і неорганічних (криогенних) рідин, наведено на рис.22.2...22.7. Результати узагальнення показують, що дослідні точки розміщуються біля лінії, яка описується рівнянням

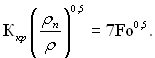(22.7)

У відповідності з цим узагальнена залежність для q_кр у безрозмірній формі виражається наступним чином:

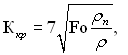(22.8)

а відповідне розрахункове рівняння для q_кр має достатньо простий вид

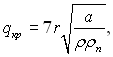(22.9)

де q_кр – критична густина теплового потоку, Вт/м², r – теплота пароутворення, Дж/кг.

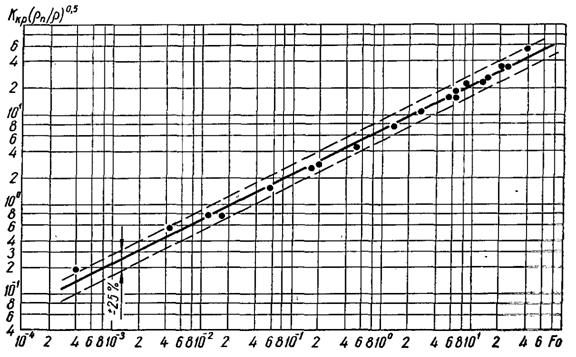
Рис.22.2. Узагальнення дослідних значень q_кр для води в інтервалі тисків 0,1...20,6 МПа [суцільна лінія – розрахункові значення по (22.8)]

Розрахунки за формулою (22.8) критичних густин теплових потоків для води, органічних і криогенних рідин показали, що залежностями f = f (П), наведеними на рис.22.1, можна користуватися у широкому діапазоні зміни тиску.

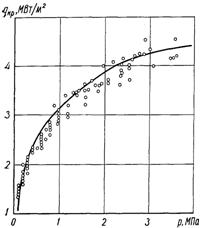
Рис.22.3. Співставлення залежності (суцільна лінія) q_кр = q_кр(р) розрахованій за (22.9) з дослідними даними для води

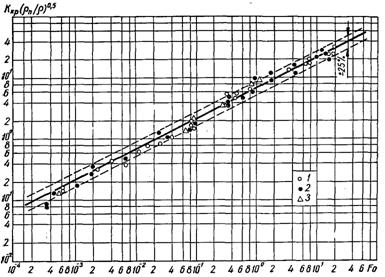
Рис.22.4. Узагальнення дослідних значень q_кр для етанолу (1), метанолу (2) і пропанолу (3) при тисках р, МПа: 1 – 0,1...6,0; 2 – 0,1...6,4; 3 – 0,1...2,3 [суцільна лінія – розрахункові значення по (22.8)]

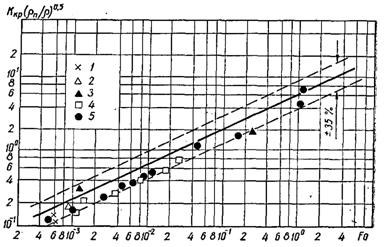
Рис.22.5. Узагальнення дослідних значень q_кр для СCl₄ (1), ацетону (2) і фреонів Ф-12 (3); Ф-11 (4); Ф-113 (5) при тисках р, МПа: 1, 2 – 0,1; 3 –0,1 і 1,0; 4 – 0,1...0,5; 5 – 0,06...2,6 [суцільна лінія – розрахункові значення по (22.8)]

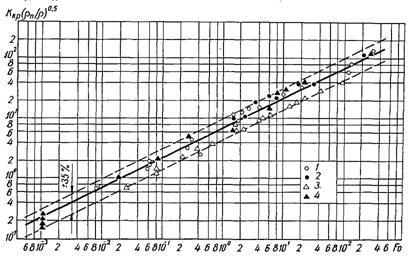
Рис.22.6. Узагальнення дослідних значень q_кр для вуглеводних – пентану (1); пропану (2); метану (3) і бензолу (4) при тисках р, МПа: 1 – 0,2...3,3; 2 – 2,1...3,3; 3 – 0,2...4,3; 4 – 0,1...4,7 [суцільна лінія – розрахункові значення по (22.8)]

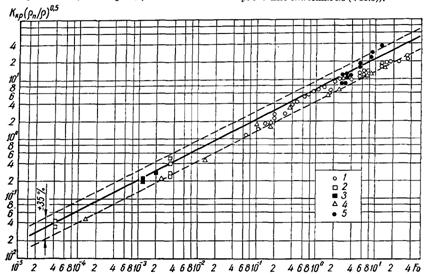
Рис.22.7. Узагальнення дослідних значень q_кр для криогенних рідин – гелію (1); азоту (2); кисню (3); водню (4) і двоокису вуглецю (5) при тисках р, МПа: 1 – 0,02...0,24; 2 – 0,01...1,1; 3 – 0,15; 4 – 0,007...1,1; 5 – 3,4...7,0 [суцільна лінія – розрахункові значення по (22.8)]

Отримані на загальних засадах (з урахуванням періодичності внутрішніх характеристик процесу бульбашкового кипіння) рівняння (20.21) і (22.8) дають можливість розв’язувати важливі практичні задачі визначення коефіцієнтів тепловіддачі при кипінні a і критичних густин теплового потоку q_кр в умовах вільного руху. У зв'язку з цим очевидна доцільність подальших досліджень внутрішніх характеристик процесу кипіння взагалі і окремо частоти утворення парових бульбашок. Не дивлячись на обмеженість даних про d_в і f, все ж можна отримати задовільні наближені рішення задачі з визначення q_кр при кипінні різних рідин. Це дає підставу вважати, що запропонований метод, рівняння подібності (22.8) і розрахункова формула (22.9), маючи певну спільність, правильно відображають фізичні закономірності процесу і впливу на q_кр основних визначальних факторів.

22.3. Криза тепловіддачі при раптовому підвищенні теплового навантаження

Для забезпечення тривалої і безпечної експлуатації теплообмінних установок і апаратів зі змінним тепловим режимом необхідно знати закономірності виникнення кризи тепловіддачі при кипінні у нестаціонарних умовах.

Виконані дослідження при експоненціальному рості потужності q_e = = q₀exp t/t₀ на тонких пластинах при кипінні води, до настання стабільного розвитку плівкового кипіння короткочасно спостерігалися густини теплового потоку, які перевищували q_кр у декілька разів (експоненціальний період t₀ = 0,5...80 мс). У режимі плівкового кипіння дослідна ділянка руйнувалася. Таким чином, була виявлена можливість реалізації на елементі нагріву густин теплового потоку більших за q_кр на протязі малого проміжку часу без значного перегріву поверхні. Зі збільшенням t₀ досягнуті теплові потоки асимптотично наближалися до q_кр. Кінозйомка нестаціонарного процесу показала, що плівковому кипінню передувало бульбашкове. Підвід потужності за степеневим законом і законом квадрату параболічного секанса не змінив якісно картину перехідного кипіння.

Реалізація названих законів зміни потужності припускає, по-перше, наявність початкового тепловиділення q₀, по-друге, значний ріст темпу підводу потужності в міру її зростання, по-третє, безмежне зростання виділення енергії на дослідній ділянці.

Для дослідження нестійких процесів виділення тепла найбільш простий і зручний ступінчатий підвід потужності, коли потужність збільшується стрибками (“накидається”) від нуля до певної кінцевої величини q_e (потужність, що виділяється в елементі, віднесена до поверхні теплообміну). При цьому, стрибкове і квазістаціонарне виділення енергії є граничними для всіх випадків, характеризуються величиною дq_e/дt і обмеженим значенням енергії. Тому при визначенні надійності теплотехнічних пристроїв можна не розглядати у кожному випадку конкретні закони виділення енергії. Достатньо знати закономірності процесу при квазістаціонарному і ступінчатому виділенні потужності в нагрівачі.

Граничним режимом ступінчатого підводу енергії є ударний, чи імпульсний, тепловий режим. Цей режим передбачає настільки швидкий нагрів рідини, що наявність на поверхні нагріву і в рідині готових центрів пароутворення не перешкоджає збільшенню температури рідини до температури, яка необхідна для інтенсивного утворення спонтанних парових скуплень. Такий процес зв’язаний з граничним перегрівом рідини до межі її метастабільного стану. Граничний перегрів за своєю природою визначає термодинамічну кризу стійкості рідкої фази.

Дослідження закономірностей теплообміну в умовах ступінчатого підводу потужності виконані в експериментах з водою в діапазоні тиску 0,02...1,0 МПа з недогрівом 0...80 К (р = 0,1 МПа) при цьому значення критичного теплового потоку співпадали з першою критичною густиною теплового потоку q_кр (за величину нестаціонарної критичної густини теплового потоку q_кр.н приймалося мінімальне значення q_e, при якому відбувалася криза тепловіддачі після ввімкнення джерела нагріву досліджуваного елементу).

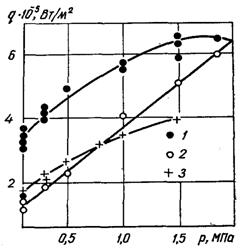
Рис.22.8. Залежність q_кр (1),q_кр.н (2) і q_кр2 (3) від тиску при кипінні ацетону на вертикальному вольфрамовому нагрівачі (D = 0,4 мм)

Під час роботи з органічними теплоносіями спостерігалася значна різниця між q_кр.н і q_кр. Зі збільшенням тиску і недогріву густина теплового потоку q_кр.н наближалася до q_кр. Вище певних значень тиску і недогріву значення q_кр.н і q_кр повністю співпадали.

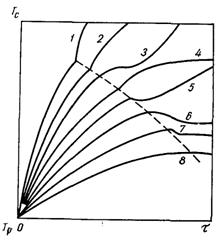
Рис.22.9. Діаграма нестаціонарних температурних режимів (криві 1, 2,...,8 відповідають q_e(1), q_e(2),..., q_e(8); q_{e(і –1)} > q_e(і))

Результати вимірів температури тонких нагрівальних елементів (із нікелю D = 0,5 мм і вольфраму D = 0,4 мм), які одночасно є термометрами опору, при р = 0,1 МПа наведені схематично на рис.22.9. Потужність “накиду” змінювалася у широких межах від такої, що відповідала початку кипіння у стаціонарних умовах, до величини, що значно перевищувала першу критичну густину теплового потоку.

У початковий момент температура нагрівача була рівна температурі рідини Т_р. При “накиді” потужності q_e < q_кр.н температура нагрівача досягала максимуму, а далі зменшувалася до значення Т_стац, яка відповідала стаціонарному режиму бульбашкового кипіння (криві 6...8). При “накидах” потужності q_e ≥ q_кр.н для ацетону і етанолу в деякий момент спостерігається зміна у темпі росту температури (криві 1, 2, 4) а у води і етиленгліколю після короткочасного сповільнення темпу росту температури відбувається її подальше зростання (криві 3, 5).

Синхронна із записом осцилографа температури поверхні кінозйомка процесів при q_e ≥ q_кр.н показала наступне. Початок пароутворення співпадає з моментом зміни темпу росту температури. Пароутворення у всіх випадках відбувається на активних центрах. Із-за високої швидкості росту парових бульбашок, пов’язаній з високим перегрівом пристінного шару, в рідині виникають значні інерційні сили. Тому на початковій стадії росту бульбашки дуже деформовані і мають великі поперечні розміри у порівнянні із стаціонарними умовами – бульбашка перетворюється у локальні парову плівку.

Чим більша величина q_e, тим більших значень досягає температура поверхні нагріву в момент початку пароутворення Т_н.п і тим менше необхідно часу для її досягнення t_н.п (штрихова лінія на рис.22.9).

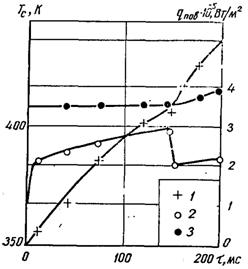
Рис.22.10. Нестаціонарні температура і густина теплового потоку при кипінні етанолу на вертикальному нагрівачі з вольфраму (D = 0,4 мм; q_e = 0,35 МВт/м²; р = 0,1 МПа): 1 – температура; 2 – густина теплового потоку; 3 – виділення енергії нагрівачем

На рис.22.10 як приклад наведені характерні зміни температури поверхні і миттєвої поверхневої густини теплового потоку q_пов при “накиді” потужності q_e > q_кр.н:

(22.10)

де Н – теплоємність нагрівача, віднесена до поверхні теплообміну.

З активацією центрів пароутворення можливе як зменшення температури (q_e < q_кр.н), так і її підвищення (q_e ≥ q_кр.н), яке у першому випадку приводить до бульбашкового режиму кипіння, а в другому – до плівкового кипіння.

Причиною нестаціонарної кризи тепловіддачі при кипінні є: по-перше, значні перегріви поверхні нагріву і пристінного шару рідини до активації центрів пароутворення; по-друге, відмінності у нестаціонарних умовах росту парових утворень у порівнянні з стаціонарним режимом.

Режими теплообміну під час нестаціонарного процесу виділення тепла за порядком проходження повторюють квазістаціонарні, а саме: теплообмін шляхом теплопровідності, природної конвекції, теплообмін при бульбашковому кипінні і далі – при плівковому режимі кипіння. У ряді випадків деякі з режимів тепловіддачі можуть бути чи недостатньо розвиненими, чи взагалі бути відсутніми. Густина теплового потоку q_пов, яка відповідає початку фазового переходу, як показують розрахунки, менші “накиду” величини q_e; крім цього, вона, як і температура початку пароутворення, залежить від q_e. Те саме можна сказати про густину теплового потоку і температуру поверхні, за яких розпочинається криза тепловіддачі. У цьому суттєва відмінність нестаціонарного переходу від бульбашкового режиму кипіння до плівкового.

Таким чином, при різкому підвищенні теплового навантаження характеристикою, яка відображає умови настання “нестаціонарної” кризи тепловіддачі при кипінні, є “нестаціонарна” критична густина теплового потоку q_кр.н. Величина q_кр.н відносно просто визначається в дослідах і зручна для використання на практиці. Результати вимірювання нестаціонарних значень температури поверхні нагріву для води і ацетону в діапазоні тиску 0,1...1,65 МПа (q_e = const) і для ацетону при р = 1,65 МПа (q_e = var), показали наступне. Із збільшенням тиску зменшується час t_н.п і різниця температур Т_н.п – Т_н. У тих випадках, коли нестаціонарні процеси виділення тепла не супроводжуються кризою тепловіддачі при кипінні, зі збільшенням р зменшується різниця температур Т_н.п – Т_стац. Така зміна температури свідчить про те, що з ростом тиску до моменту початку пароутворення кількість теплоти, яка акумульована як у самому нагрівачі, так і в пристінному шарі, зменшується. Наслідком цього є зменшення швидкості випаровування рідини в перші парові бульбашки. Крім цього, внаслідок збільшення густини пари зменшується швидкість росту парових бульбашок. Вони менше деформуються, і форма їх більше наближається до характерної для стаціонарних режимів.

Отже, з підвищенням тиску закономірності проходження нестаціонарних процесів виділення тепла наближаються до квазістаціонарних. Це є причиною зменшення різниці в значеннях q_кр і q_кр.н.

Виміри нестаціонарних значень температури нагрівача при р = 0,1 МПа для води, ацетону і етиленгліколю у діапазоні температур рідини 15...20 °С до температури насичення (q_e = const) і для ацетону і етиленгліколю при DТ_нед = const. З ростом недогріву збільшується час t_н.п, тому що необхідно більше часу на нагрівання поверхні нагріву і пристінних шарів рідини до рівня температур, які необхідні для активації центрів пароутворення. При цьому збільшується температура Т_н.п, а різниця температур Т_н.п – Т_стац зменшується. Наслідком цього є відносне зменшення кількості акумульованої теплоти як у нагрівачі, так і в пристінному шарі рідини, яка реалізується в початковий період на випаровування рідини у парові утворення. З активацією центрів пароутворення закономірності росту перших парових утворень наближаються до закономірностей їх росту в стаціонарних умовах.

Відмічені зміни у характері проходження нестаціонарних процесів виділення тепла зі збільшенням недогріву призводять до виродження нестаціонарної кризи тепловіддачі при кипінні.

Вплив теплоємкості нагрівача на нестаціонарну кризу тепловіддачі при кипінні досліджувався рядом експериментаторів. Для води при різних теплоємкостях нагрівача не виявлено відмінності q_кр.н від q_кр. Для органічних рідин q_кр.н і q_кр значно відрізняються, особливо при малій еквівалентній товщині елементу d_екв ( де D і d – зовнішній і внутрішній діаметри нагрівача). Із збільшенням d_екв збільшується акумулятивна здатність нагрівача, яка перешкоджає швидкому підвищенню температури поверхні нагріву. Критичні густини теплового потоку q_кр.н і q_кр наближаються один до іншого (рис.22.11).

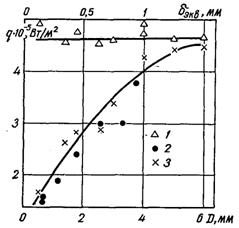
Рис.22.11. Залежність q_кр і q_кр.н від розміру вертикального дослідного елементу (сталь Х18Н9Т) при кипінні етанолу (р = 0,1 МПа): 1 – q_кр (стрижні); 2 – q_кр.н (стрижні); 3 – q_кр.н (трубки D = 5 мм з різною товщиною стінки)

Результати дослідження залежності q_кр.н від діаметра суцільного циліндричного добре співпадають з дослідними даними для циліндричних трубок.

Із збільшенням тиску незалежність q_кр.н від форми і поперечних розмірів нагрівача зберігається, і q_кр.н також визначається тільки d_екв. Зі збільшенням теплоємкості елементів значення q_кр.н = f(р) розташовуються все ближче до q_кр = j (р) і спів падання q_кр.н і q_кр відбувається при менших тисках.

При вивченні нестійких режимів плівкового кипіння і зворотних переходів від плівкового кипіння до бульбашкового – другі критичні густини теплового потоку q_кр2, виявлено, що у випадку q_кр2 > q_кр.н (тонкі дротики) (див. рис.22.8) початкове з’явлення плівкового режиму кипіння обов’язково зміниться з часом на бульбашкове кипіння. Хоч виникле плівкове кипіння і носить нестійкий характер, але воно може призвести до руйнування поверхні нагріву. Якщо q_кр.н і q_кр2, то навіть при виникненні локальних парових плівок плівкове кипіння буде стабільним і розповсюджуватися по всій поверхні нагріву. На нагрівачах великих розмірів (d_екв) завжди виконується умова q_кр.н > q_кр2.

Існування розвинених гідродинамічного і теплового пограничних шарів, що є наслідком початкового виділення тепла до набору потужності, чинить суттєвий вплив на початок нестаціонарної кризи тепловіддачі при кипінні (рис.22.12).

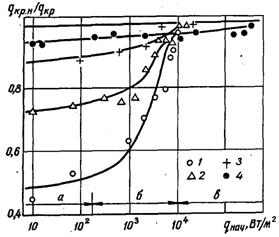
Рис.22.12. Сумісний вплив q_поч і d_екв на q_кр.н при кипінні етанолу (р = 0,1 МПа) на вертикальних трубках (накид потужності при режимах: а – вільного ламінарного руху; б – турбулентного руху; в – кипіння) при d_екв, мм:1 – 0,28; 2 – 0,64; 3 – 0,93; 4 – 1,25

Розрахунок умов теплообміну до накиду потужності уможливлює виконати аналіз причин і характер такого впливу. Межа вільного ламінарного режиму руху біля нагрітої вертикальної стінки з незначною тепловіддачею відповідає q_поч = 150...200 Вт/м² (див. рис.22.12). У цьому випадку для нагрівачів різної теплоємкості зміни гідродинамічних і теплових умов у пристінному шарі рідини у порівнянні з q_поч = 0 незначні і мало впливають на q_кр.н. З настанням перехідного і вільного турбулентного руху при підвищенні q_поч різко зростає інтенсивність дії початкового вільного руху на проходження неусталених процесів. Нестаціонарна криза кипіння настає при значно більших накидах потужності. З настанням кипіння рідина вже настільки сильно початково подразнена, що накид потужності не веде до кризи при q_e < q_кр.

Зі збільшенням еквівалентної товщини стінки помітний ріст нестаціонарних критичних густин теплового потоку в залежності від q_поч починається в області одних і тих же початкових теплових потоків При сумісному впливі початкового виділення тепла і тиску на нестаціонарну критичну густину теплового потоку характер залежності q_кр.н/q_кр від q_поч подібний отриманій при р = 0,1 МПа. При підвищенні тиску величини q_кр і q_кр.н зближуються.