ДОДАТКИ
Д.1. Різні способи задавання граничних умов
1. Гранична умова першого роду зводиться до завдання розподілу температури на поверхні тіла у довільний момент часу, тобто
Тст(t) = f(t), (Д.1)
де Тст(t) – температура стінки поверхні.
2. Граничні умови другого роду зводяться до завдання густини теплового потоку для кожної точки поверхні тіла як функції часу, тобто
qст(t) = f(t). (Д.2)
Найпростіший випадок це коли густина теплового потоку
qст(t) = qср = const, (Д.3)
де qср – густина теплового потоку середовища, обмежуючого тіло.
Такий випадок теплообміну має місце при нагріванні тіл у високотемпературних печах, де передача тепла відбувається випромінюванням і підпорядковується закону Стефана – Больцмана, коли температура тіла значно менша температури випромінюваних поверхонь.
3. Граничні умови третього роду зазвичай характеризують закон конвективного теплообміну між поверхнею тіла і навколишнім середовищем при усталеному потоці тепла. У цьому випадку кількість тепла, яке передається в одиницю часу з одиниці площі поверхні тіла в навколишнє середовище з температурою Тср у процесі охолодження (Тст > Тср), прямо пропорційне різниці температур між поверхнею тіла і навколишнім середовищем, тобто
qст = a(Тст – Тср), (Д.4)
де a – коефіцієнт тепловіддачі, Вт/(м2·К).
4. Граничні умови четвертого роду відповідають теплообміну поверхні тіла з обмежуючим середовищем (конвективний теплообмін тіла з рідиною) чи теплообміну контактуючих твердих тіл, коли температура контакту поверхонь однакова. При обтіканні твердого тіла потоком рідини (газу) передача тепла від рідини (газу) до поверхні тіла на незначній відстані від поверхні тіла відбувається по закону теплопровідності, тоді
Тст(t) = [Тср(t)]ст.. (Д.5)
Крім рівності температур, має місце рівність потоків тепла, тобто
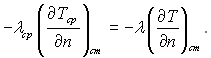 (Д.6)
(Д.6)
Таким чином, при конвективному теплообміні твердого тіла з рідиною у випадку стаціонарного температурного поля (дТ/дt = 0) користуються граничною умовою третього роду, а у випадку нестаціонарного температурного поля (дТ/дt № 0) необхідно при точному рішенні задачі застосовувати граничні умови четвертого роду [співвідношення (Д.5) і (Д.6)]. У випадку нестаціонарного променевого теплообміну необхідно застосовувати граничні умови другого роду [співвідношення (Д.2)]. При малих різницях температур, коли [Тст(t) – Тср(t)] ® 0, можна використовувати закон Ньютона, тобто граничні умови третього роду. При цьому величина a позначати коефіцієнт променевого теплообміну [a = a(Т) = const].
Д.2. Формули температурного поля і густини теплового потоку для необмеженої плоскої стінки при qV = const (рис.2.1)

Закінчення таблиці Д.2

Д.3. Формули температурного поля лінійного теплового потоку для необмеженого полого циліндра при qV = const (рис.2.2)

Продовження таблиці Д.3

Закінчення таблиці Д.3

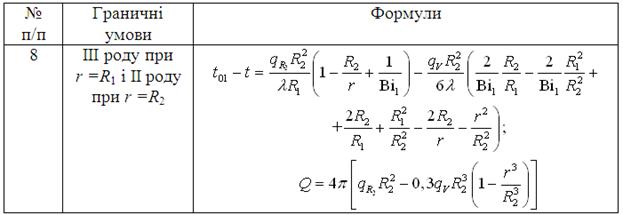
Д.4. Формули температурного поля і поля теплового потоку для полої кулі при qV = const (рис.2.3)

Продовження таблиці Д.4

Продовження таблиці Д.4

Закінчення таблиці Д.4
Д.5. Коефіцієнти теплопровідності матеріалів покривного шару
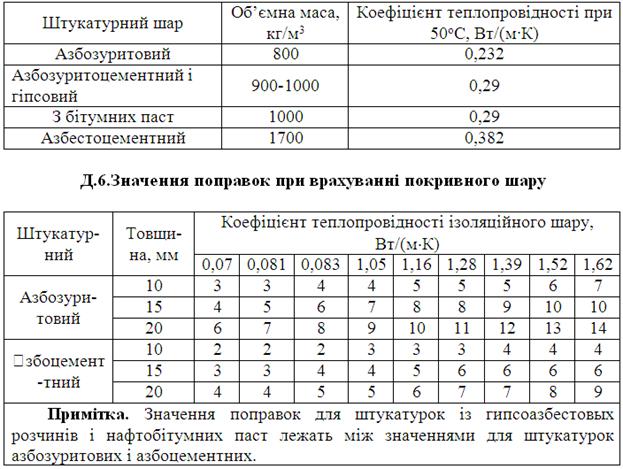
Д.7. Гранична товщина ізоляційних конструкцій паропроводів

Д.8. Коефіцієнти теплопровідності теплоізоляційних матеріалів
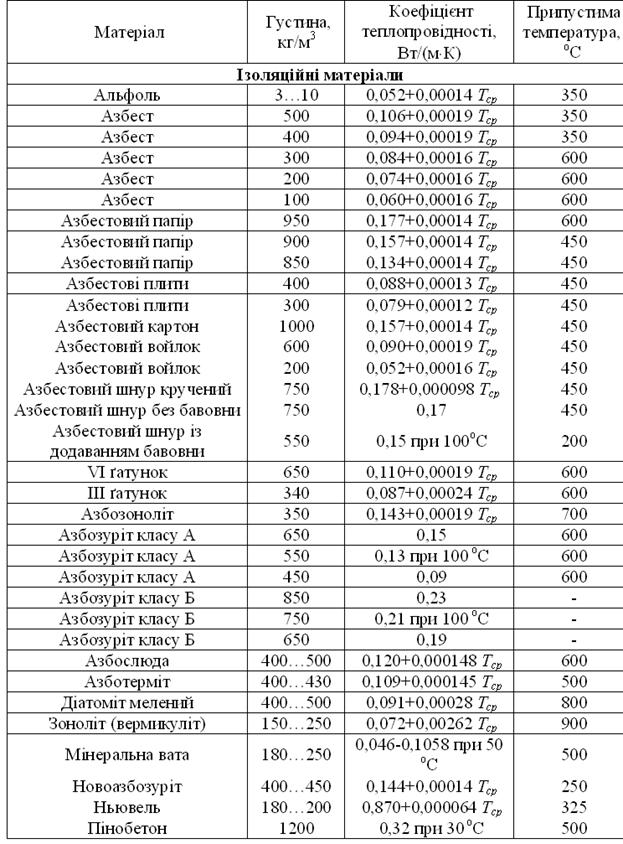
Закінчення таблиці Д.8
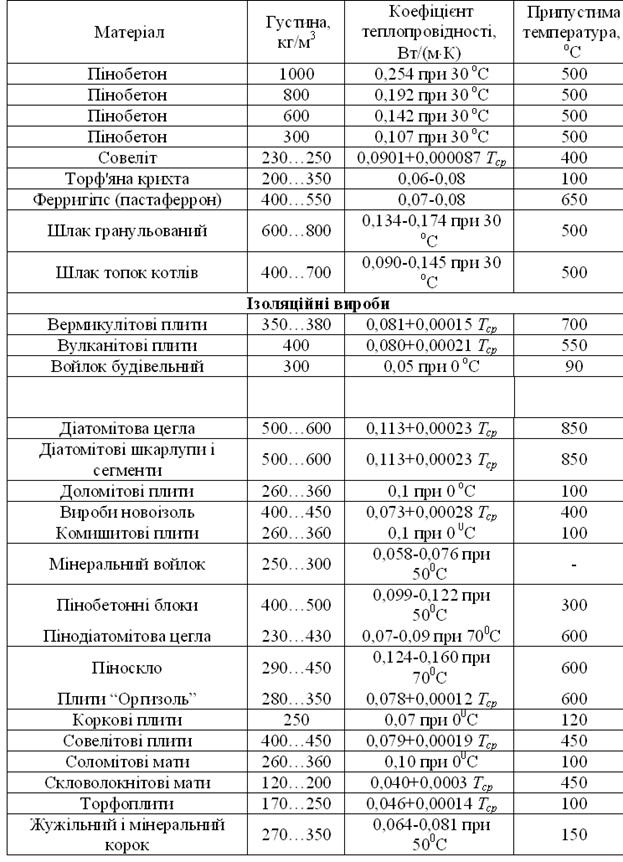
Д.9.Коефіцієнти теплопровідності сталі
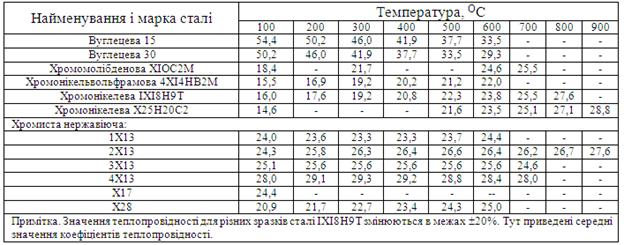
Д.10. Коефіцієнти теплопровідності металів і сплавів
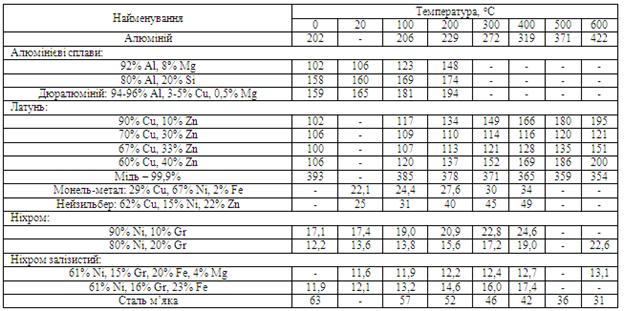
Д.11. Коефіцієнти теплопровідності сплавів
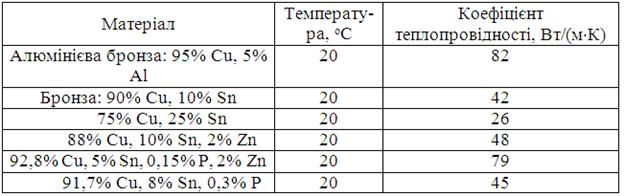
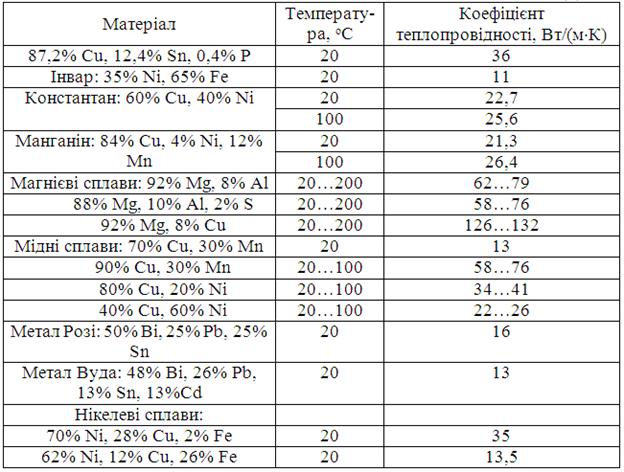
Закінчення таблиці Д.11
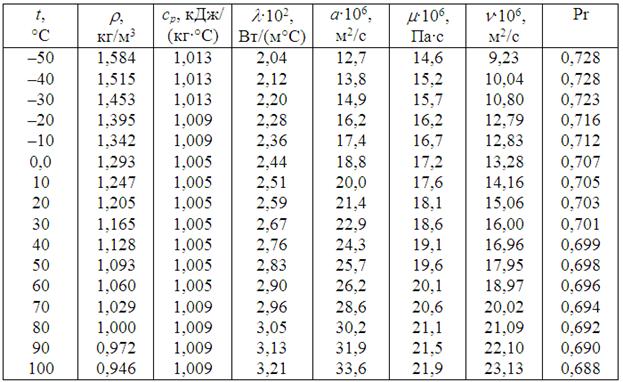
Д.12. Фізичні властивості сухого повітря (В = 760 мм рт. ст. = 101 кПа)
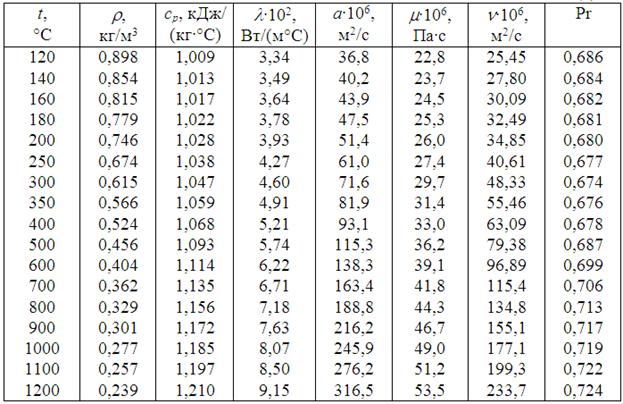
Закінчення таблиці Д.12
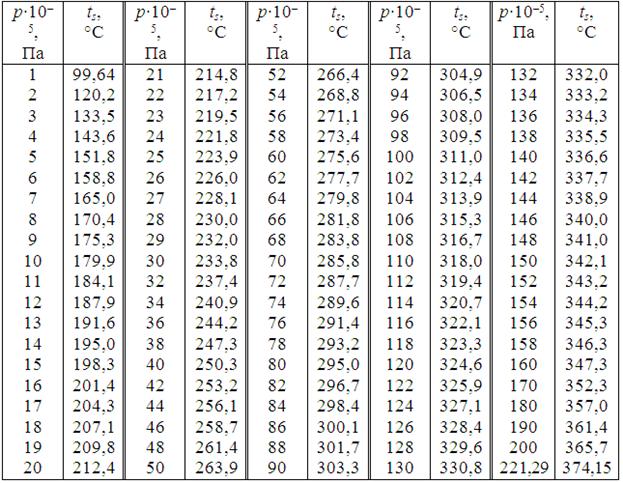
Д.13. Температура кипіння води у залежності від тиску